整体式桥台斜交梁桥地震反应研究

黄 朝 光

(福州市交通建设集团有限公司, 福建 福州 350007)

对于中小梁式桥，整体式桥台桥梁不用设置伸缩缝桥梁，特别避免在地震中发生落梁，目前在国外应用较多。然而整体式桥台桥梁的计算涉及到复杂的结构-土共同作用[1-2]，目前的设计仍然以经验为主，国内一直缺少统一的标准，而国外在设计方法和构造中都与国内规范不同。目前无缝桥抗震性能的研究已广泛开展，整体式无缝桥在地震反应分析时土和结构的相互作用不可忽略[3]。在对整体式桥台进行施工中，梁台后填土基本类型及其压实度将会给无缝桥结构带来比较大的影响，而基础刚度影响较小[4-5]。文献[6]对土体具体的密实情况、桩侧图以及后填土对于整体形式桥梁在动力方面的特征影响进行研究。梁才[7]针对斜交梁桥斜交角发生的变化进行分析，并研究了受力情况对无缝桥主梁部位的影响。另外，在当今的很多二次开发项目中，土体动力的实际本构模型也为考虑土-结构动力相互作用的有限元研究提供了基础[8]。通过研究对比发现，无缝桥梁的抗震性能比一般设置伸缩缝的桥梁更好[9]。目前对于无缝桥梁的土-结构以及上部结构的简化模型已经较为成熟[10-14]。有研究者通过考虑土-整体式桥台结构动力相互作用的分析，发现台后翼墙或者耳墙等结构的侧向压力较大，可能是由于台后土压力使其上部结构产生了水平方向的旋转，导致梁体之间容易产生相互错位，而搭板也可能发生横移[15-20]。

从前述研究可看出，台后压力的变化对整体式桥台桥梁，特别是斜交情况下的桥梁的抗震性能有较大影响，因此应将土和结构的相互作用当作一个整体来研究。而采用库仑土压力法或者借助于温克勒弹性，无法考虑地基所受到的实际破坏及其对相应结构的影响。为了能够考虑桥台周围近场土的塑性影响，分别建立了土-整体式斜交梁桥三维有限元计算模型和基于p-y曲线的简化桩土模型，比较了两种模型分析的结果，研究了整体斜交桥的地震反应规律。

1 工程背景

整体式桥台斜交桥梁如图1(a)所示，采用3 m×16 m预应力混凝土空心板作为上部结构，宽度11.55 m，梁高0.8 m，斜交角为15°。预制空心板梁采用C40混凝土，桥台(墩)与主梁刚性连接。下部基础如图1(b)和图1(c)所示，桥台盖梁截面大小是1.2 m×1.6 m，桥墩的实际直径是1 m。盖梁的截面大小是1.1 m×1.3 m，将钻孔形式的灌注桩作为基础，配筋如图1(d)所示。台后填土采用内摩擦角40°的粗砂砾，密度为1 950 kg/m3。土层参数及分布情况如表1所示。

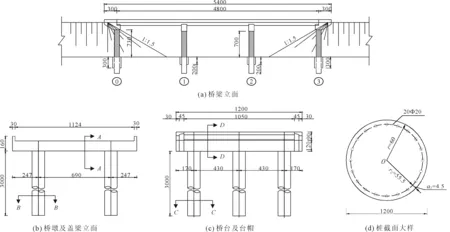
图1 总体桥梁布置图(单位：mm)

表1 土层的具体分布情况及其参数

从图2可知，本次对Kobe波、Loma perita波以及El Centro波这三种频谱各异的地震波进行选择和应用。在斜交桥上，空间所承受的力十分复杂，因此该桥梁属于不规则形式的桥梁，根据已有研究，为了得到斜交桥最大内力和变形，通常考虑沿x向和y向输入地震波[21-25]，如图3所示。考虑了三种地震波在具体输入过程中的工况，沿着x方向进行地震波输入，沿着方向进行地震波输入，或者是沿着x方向和y方向同时进行地震波输入，输入地震波方向及观测点编号如图3所示。

图2 地震波加速度时程

图3 地震波的输入方向及其位置编号分析

2 整体有限元模型与简化模型

2.1 整体形式模型建立

在具体的模型建立中，首先应对考虑土和结构动力相互作用形式的模型进行建立，并将一层具有粘弹性特征的人工边界单元施加在外侧。考虑周围场地土在内，建立了土-整体式斜交桥梁结构三维有限元模型，具体情况见图4。

图4 斜交桥整体模型

(1)

(2)

其中:cs和cp分别表示介质剪切波和P波波速；αt，αn分别表示切向和法向人工边界修正系数；切向弹簧刚度用Kb表示，法向弹簧刚度用Kbn表示；切向阻尼系数用Cbt表示，法向阻尼系数用Cbn表示；介质实际的剪切模量用G表示；介质实际的质量密度用ρ表示；地震波源和人工边界点之间的距离用R表示。 为等效泊松比，可以根据下式取值：

(3)

(4)

斜交桥的上部结构为梁格体系，桩基础采用非线性梁单元模拟，桥台采用实体单元，设置接触单元，使得桥台与台后土之间只产生压力。考虑材料各向同性硬化或者软化，根据ABAQUS软件中具有的Mohr-Coulomb这一弹塑性形式的模型，对土体材料所具备的非线性进行模拟[22]。非线性梁单元的材料本构采用纤维模型[26]。整体模型由于人工边界的添加，模型减小幅度比较大，但是因为三维模型中仍然有着很多的单元数量，而且涉及到土体非线性，本次主要通过ABAQUS的平行模块进行模型建立，并在此基础上进行相应的计算。

2.2 p-y弹簧模型

通过“p-y”这一方法，通过一系列具有独立性特征的非线性弹簧对台后土以及桩侧土进行了刚度模拟，考虑桩土动力相互作用[12]。桩侧土弹簧使用了美国石油协会API(2000)推荐的“p-y”曲线模拟。砂性土相关取值如图5所示。

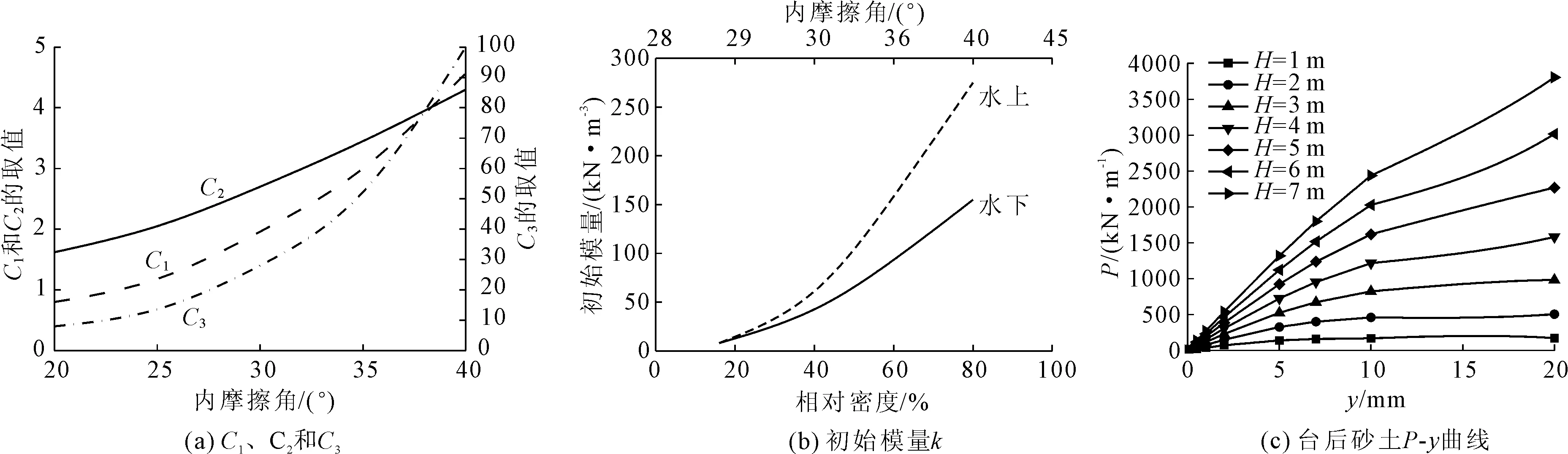
图5 砂性土p-y参数

在本次台后土曲线的绘制过程中，主要应用的是美国国家公路合作研究计划设计手册(2012)中的方法。在对实际工程进行计算的过程中，台后土属于具有密实性特征得到砂性土，经过计算获得的后填土被动压力系数K和桥台位移与桥台高度比之间的关系，图6是代表其关系的曲线图，在图中，桥台发生的位移用Δ来表示，桥台实际的高度用H来表示。

图6 台后土所承受的压力

3 两种模型中的时程反应对比分析

图7和图8分别给出了随深度变化，桥墩和桥台的桩基础内力和位移。通过比较可以看出，采用整体模型，计算得到的内力分布与土层性质改变相关性更为显著。此外，采用弹簧模型计算得到的位移小于整体模型中桥墩及其桩基础的位移。不同峰值地震作用下的弹簧模型和整体模型桥墩及其桩基础的变化规律一致，通常墩顶的内力和位移最大。整体上看，采用土-结构模型的整体对内部受力情况和位移情况计算的结果比通过弹簧模型进行计算所获得的结果大。在桥墩顶部的受力计算中，这两种模型计算有着最大的结果差异。采用弹簧模型，可以发现，随着峰值的增加，内力所发生的变化和线性增加十分接近，在进入到了0.2g这一地震之后，台厚土也进入到了塑形阶段，而弹簧模型依然是线性变化。

4 整体式桥台斜交桥梁地震反应

研究发现不同地震波作用下的规律基本相同，图9仅给出了El Centro波影响之下的桥台峰值应力具体分布情况。通过该图可以发现，在桥台桩顶部普遍存在应力集中，斜交桥桥面板钝角(即图3中的S1与x7位置)处桥台应力可达到锐角位置应力的2倍左右，当峰值所具有的加速度带了2.0g的情况下，桥台所承受的应力也就增大较多，此时台后土进入塑形，刚度减小，桥台的应力增长。从图中可以看出，桥台应力的三个集中位置，其应力分布不均。由于整体式桥台桥梁的桥台和上部结构连接在一起，上部结构的地震反应、桥台刚度的退化，都会同时引起桥台受力的不利，钝角处的桥台与主梁连接处应考虑相应的加固措施。

图7 El Centro波影响作用下桥墩和桥桩基础内力变化及其位移峰值

图8 El Centro波影响下桥台和桥桩基础内部受力及其位移峰值

图9 桥台Mises峰值在El Centro地震波影响下所呈现出的应力云图(单位:Pa)

图10给出了El Centro地震波峰值达到0.2g的情况下，台后土钝角位置是其主拉应力、正应力以及主压应力最大的位置。在桥台后土钝角位置，应力呈现出了明显的集中情况。桥梁上部结构，斜交板发生了向桥台钝角处的扭转。可以看出，0.2g峰值加速度工况下的台后土应力和0.1g峰值加速度工况下的反应相比，增长明显。钝角处台后土应力集中的面积增大，在较大范围内的应力峰值都较大，对台后搭板较为不利。通过分析可以看出，台后土的刚度变化对桥梁结构的反应有较大影响。

绘制了台后土在不同地震动峰值下的土压力-位移曲线，如图11所示。可以看出，当峰值加速度达到0.2g后，和0.1g地震波反应相比，台后土压力与位移曲线不再是线性增加。分析表明，由于台后土刚度下降，桥台和台后土之间发生了脱离。

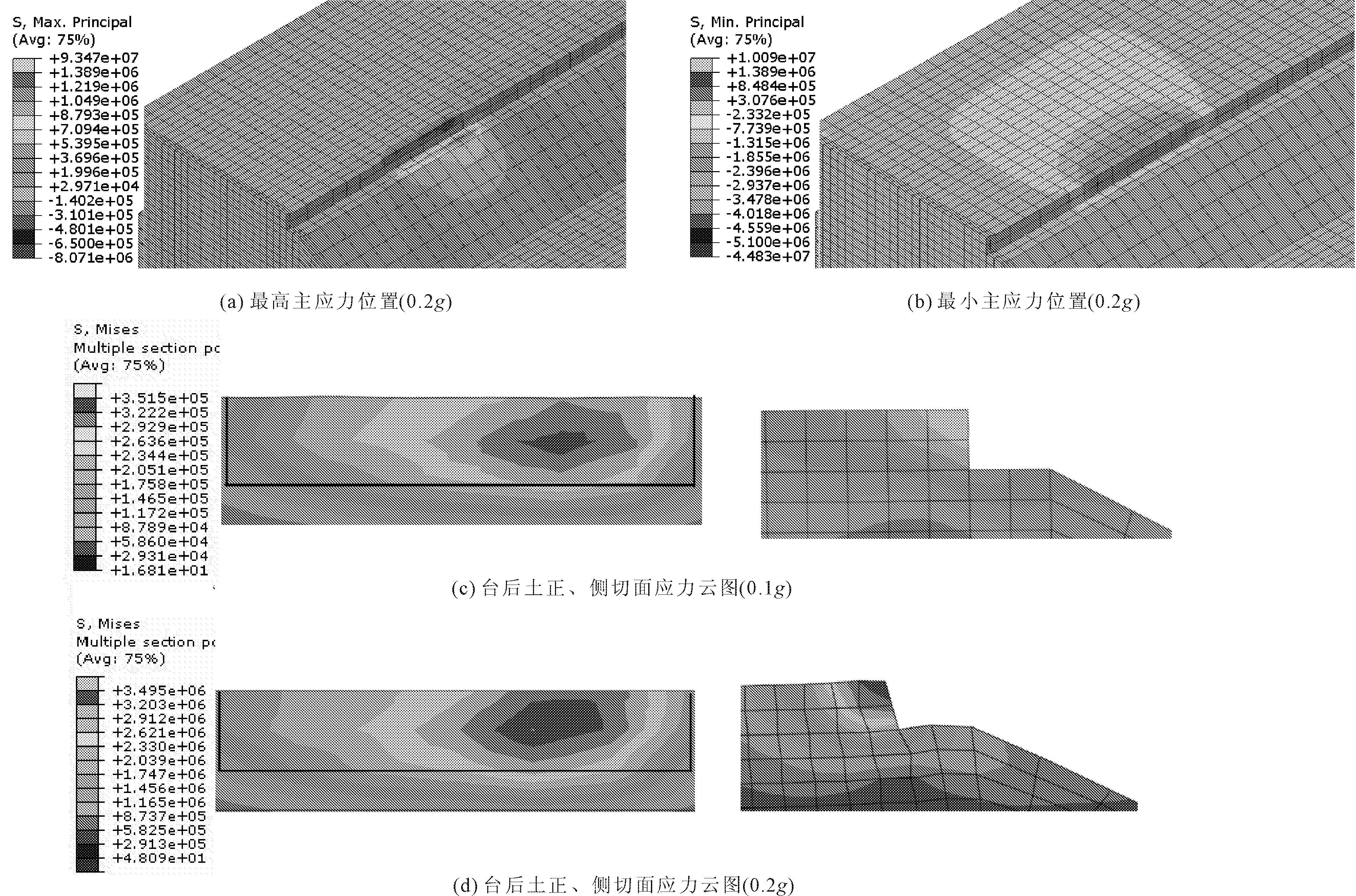
图10 应力及其变形示意图(单位：Pa)

5 结 论

(1) 在多遇地震波作用下，整体模型体现了土层刚度退化对结构产生的影响。在罕遇地震波作用下，整体模型桥墩和桩基础在罕遇地震下的内力和位移和多遇地震相比，显著增加，而弹簧模型内力变化近似于线性的增加。

(2) 在遇到罕见地震作用的情况下，桥台后填土自身的刚度将会随之下降，在整体形式斜交桥台腿脚位置以及台厚土之间也将会出现脱离现象。整体模型体现了台后土刚度退化对结构产生的影响，而在弹簧模型之中，借助于p-y这一曲线并不能将台后土在罕见地震影响下的刚度变化完全呈现出来。

图11 台后土在El Centro波影响下所承受的土压力及其位移曲线

(3) 整体式斜交桥的上部结构和桥台连接，导致台后土对上部结构约束，台后土刚度退化使得上部结构产生扭转，斜交桥钝角处的应力达到了锐角处的大约两倍。设计中可以考虑加强钝角处桥台与上部结构的连接。在遇到罕见地震的情况下，台后土自身的应力将会随之增加，其搭板区域内的应力也都会随之加大，这将会对台后土造成很大范围的影响。0.2g地震作用下，由于台后土刚度下降，台后土压力和位移不再为线性增长。