层状材料不同几何表面间隔破裂的数值研究

朱 旭, 马天辉

(大连理工大学 海岸和近海工程国家重点实验室， 辽宁 大连 116024)

间隔破裂现象是地壳岩层、岩土工程及材料工程等结构中十分常见的一种破裂现象，当材料受到应力直接作用或温缩、干缩等导致的应力间接作用时均可能发生。根据以往的实地观察及实验总结，可以按其分布形态的不同，将其分为三种破裂模式：条状间隔破裂、网状间隔破裂和环状间隔破裂(分区破裂化)[1]，其中条状间隔破裂和网状间隔破裂主要发生在层状材料结构中。层状材料表面的条状间隔破裂表现为二维的相互平行的近似等间距的裂纹，这种裂纹在混凝土路面极为常见(见图1(a))；网状间隔破裂表现为三维网状的近似等空间裂纹，按形态还可以更具体地分为梯状裂纹(见图1(b))，常见的如树皮，和网状龟裂纹，包括土地龟裂，沥青混凝土路面[2]，立柱油漆涂层干裂产生的网状裂纹(见图1(c))以及陶瓷表面因冷缩产生的龟裂(见图1(d))等。可以发现，间隔破裂现象在不同材料及不同几何表面上表现出相似的形态，具有某种规律性。

图1 间隔破裂现象示例

由于间隔破裂现象涉及的领域广泛，这一问题受到了各大领域科学家以及学者们的广泛关注。在过去的几十年里，已有很多学者围绕理解层状材料间隔破裂现象的形成机制及演化规律展开了理论[3-4]、试验[5]及数值[6]等多方面的研究。例如Thouless等[7-8]分析了基于弹性均匀系统的表面脆性薄膜在拉伸作用下形成的一系列相互平行的等间距裂纹，并提出裂缝间距与薄膜厚度的平方根成正比；Rives等[9]通过在基层上的脆性涂层中产生边缘裂缝来模拟层状岩石中的裂缝形成；Wu等[10]描述并比较了两种测量裂缝间距的方法，并对层面上的两种断裂模式进行了比较，他提出了一个重要的概念，即裂纹饱和现象，这是一种当施加的应变达到一定值时，随着应变的继续增加，裂纹间距不再增加而是趋于恒定的现象，他提出达到饱和的裂缝间距是层厚度的函数，与应变无关；2000年，Bai等[11-12]建立了带有预置裂纹的双层及三层层状材料数值模型，首次从两条相邻裂纹的应力场分布角度对间隔破裂现象形成及饱和机制进行了系统的探讨。

尽管间隔破裂现象的研究已经进行了数十年，但大多数的理论和数值分析仅考虑了二维平面模型或三维平板模型，难以揭示在不同的几何表面上形成这种相似的裂纹形态是否遵循着相同的规律。此外，现有的对于间隔破裂现象的数值分析多是基于应力分析方法进行的，很少能通过数值手段对间隔破裂过程和裂缝形态进行再现。Tang等[13]采用RFPA3D对带有非均质夹层的三层平板模型的间隔破裂过程进行数值试验取得了良好的效果。

本文旨在通过模拟不同几何表面在不同加载比及不同层厚比控制下的间隔破裂现象，进而理解其裂缝形态及控制因素的规律性，为进一步探究岩层或工程中这种规则的间隔破裂现象的形成机制提供参考。

1 数值方法和模型描述

本文采用了有限元分析系统RFPA3D[14]对不同几何面三维模型进行数值研究。RFPA3D是三维的真实破裂过程分析系统(Realistic Failure Process Analysis，RFPA)，它可以基于应力分析方法(有限元方法)和弹性损伤理论对准脆性材料(例如岩石、混凝土、陶瓷等材料)的渐进破坏过程进行模拟[15-16]。它首先将材料模型离散化成由细观单元组成的数值模型，通过韦伯分布规律对离散化后的计算模型细观单元的材料力学参数进行赋值，以描述材料的非均质性。韦伯分布的基本方程如公式(1)所示，它主要由两个参数控制：u0为单元材料力学性质参数的平均值，例如强度，杨氏模量和泊松比等；m为材料均质度指标，m越大，表示材料越均匀，反之亦然。

φ(u)=(m/u0)(u/u0)m-1×exp[-(u/u0)m]

(1)

单轴应力状态下的弹性损伤本构关系被用于描述细观单元的变形和破坏，如图2所示。对于弹脆性材料，起初这些单元都被视为弹性的，并且在达到给定的损伤阈值之前，均保持线弹性变形特征。这里最大拉应力准则和莫尔-库仑准则分别用来判断单元拉伸破坏和剪切破坏的损伤阈值。

本文主要是通过对不同几何表面产生间隔破裂现象的模拟，进而发现其规律性及影响因素。为此建立了三种几何表面的双层三维数值模型，包括平面模型、柱面模型和球面模型，以研究不同几何表面在恒定应变增量Δ的准静态加载条件下，间隔破裂的演化规律的异同。三种模型的尺寸及边界条件如图3所示，平面模型的长宽均为150 mm，柱面模型在轴向上均为200 mm长，球面模型和柱面模型最外层半径r3均为100 mm。为了研究层厚对间隔破裂形成及裂纹形态的影响，所有模型均保持基层厚度T恒为15 mm，表层厚度t变化为5 mm、10 mm、15 mm和30 mm。以5 mm表层厚度的平面模型为例(见图3(a))，该模型尺寸为150 mm×150 mm×20 mm，由450 000个(150×150×20)8节点六面体单元组成，即每个细观单元均为1 mm的小立方体，其余模型以此类推。

图2 单轴应力状态下细观单元的弹性损伤本构关系

三种模型均是在恒定应变增量Δ的准静态加载条件下产生破坏，边界条件如图3所示。根据Tang等[13]采用RFPA3D模拟三层平板模型间隔破裂过程的数值研究经验，他提出通过改变不同方向的加载比λ，可以实现非均质层的裂纹形态从平行裂纹到梯状裂纹再到多边形裂纹的连续转变。据此，本文主要研究三种不同几何表面的模型是否都可以实现裂纹形态的转变。所有模型都选取相同的表层厚度t为5 mm。

模型的材料力学参数如表1所示。由于要控制裂缝只出现在表层，限制基层中产生裂缝，双层模型中每层材料的力学参数是不同的。在本文的模型中，表层比基层均质度m低，也就是更加不均匀。表层的弹性模量E是基层的几倍，这样在同样的应变下，表层会产生更大的拉应力。此外，基层的强度设定为比表层的强度高出许多倍，这样表层就会先发生破坏。

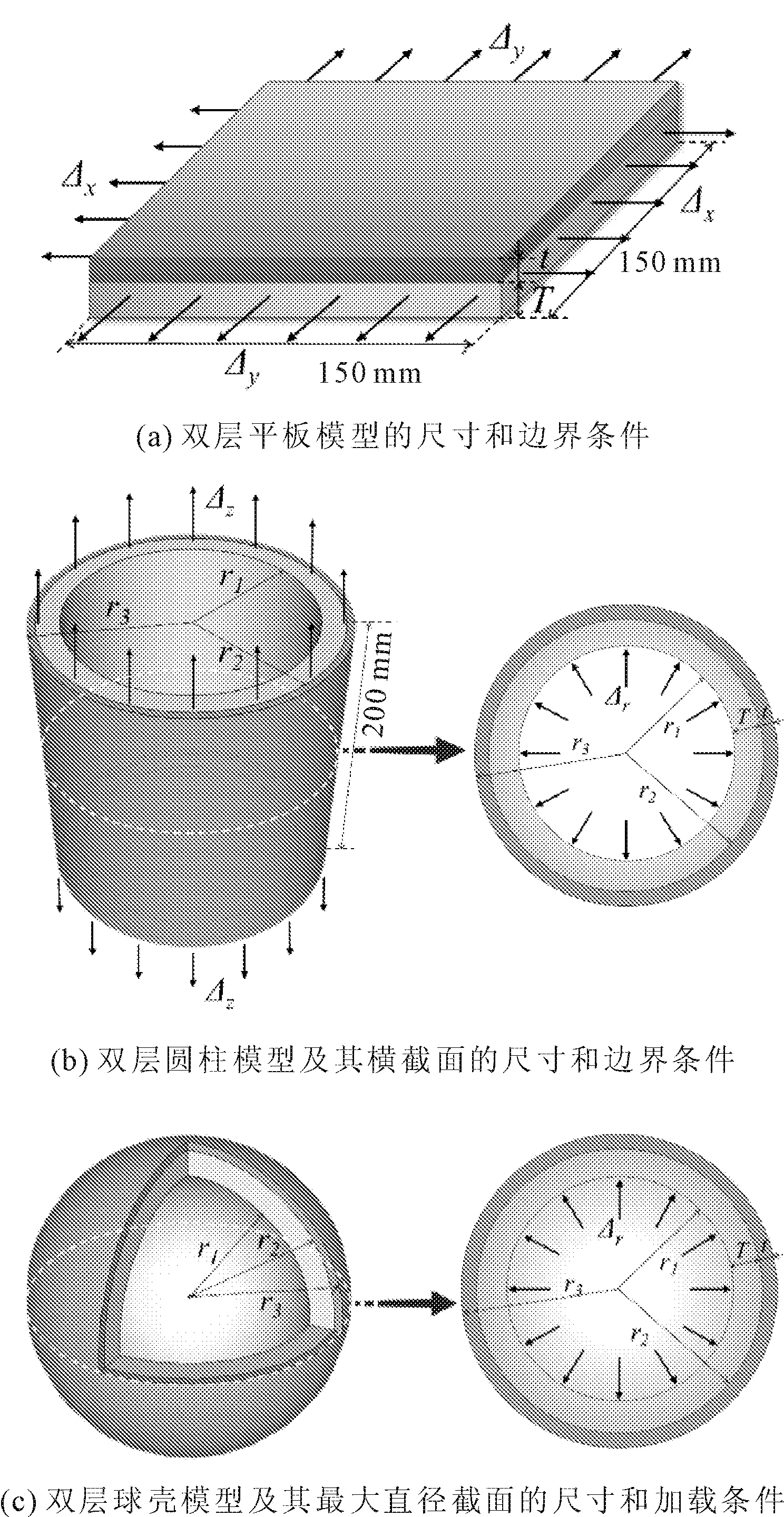
图3 三种模型尺寸及边界条件描述

表1 模型材料力学参数

2 模拟结果分析

2.1 加载比对不同几何表面间隔破裂形态的影响

在平板模型中，将λ定义为y方向上的位移增量与x方向上的位移增量的加载比(λ=Δy/Δx)，见图3(a)。分别取λ为0、1/5、1/2、1进行模拟，模拟结果见图4。在单轴拉伸的作用下(λ=0)，即模型仅在x方向被拉伸，裂缝几乎完全垂直于x方向产生，最终形成一组平行的近似等间距的裂缝(见图4(a))。而后，随着λ值的增大，逐渐出现y方向的位移增量，起初多数裂缝仍然垂直于x方向发展，但出现少数垂直于y方向的裂缝，λ值越大，垂直于y方向的裂缝越多。可以观察到，在双向拉伸作用下，即λ变化范围为0.2到0.5时，最终裂纹形态是像梯子的梯级一样分布的梯状裂缝(见图4(b)、图4(c))。当λ值变为1时，模型表面出现近似规则的多边形网状裂缝(见图4(d))。

图4 不同加载比作用下平面模型表面间隔破裂形态

类似地，在圆柱模型中，也将λ定义为两个不同方向加载增量的值-轴向上的位移增量与径向上的位移增量的加载比(λ=Δz/Δr)，见图3(b)。这里取λ为0、1、2、5进行模拟，模拟结果见图5。在加载比λ=0时，也就是此时仅有径向位移，得到的均为近似平行于轴向的等间距裂缝(见图5(a))。随着λ值逐渐从0变大，开始出现轴向的位移增量，当加载比λ=1时，得到近似规则的多边形裂缝(见图5(b))。随着λ值的继续增大，更多平行于周向的裂缝出现(见图5(c)、图5(d))。也就是说随着λ值从0到大于1的值的变化，最终裂纹形态可以实现从完全平行于轴向的平行裂缝到完全平行于周向的平行裂缝的连续过渡。

图5 不同加载比作用下柱面模型表面间隔破裂形态

然而，在球壳模型中，由于球壳表面是一个封闭的曲面，只有内外表面两个自由表面，因此它只能实现内部向外的径向扩张一种加载方式，见图3(c)，不存在不同方向加载比的变化。模拟结果见图6，球壳模型表面只能形成近似规则的多边形网状裂缝，相应地，在平面模型加载比λ=1，也就是双轴同增量拉伸时会产生多边形网状裂缝(见图4(d))。而同样仅在径向载荷作用下，圆柱模型表面则是出现平行裂缝(见图5(a))，相应地，在平面模型加载比λ=0，即单轴拉伸的情况下会产生平行裂缝(见图4(a))。因此，与平面模型的数值结果对照下，可以推测出，在球壳模型中，径向载荷导致沿着层面的双轴同增量拉伸应力，而在圆柱模型中，径向载荷则是导致沿圆周方向的单轴拉伸应力。

图6 径向载荷作用下球壳模型表面间隔破裂形态

2.2 层厚比对不同几何表面间隔破裂形态的影响

以往已有研究表明破裂层厚度是裂纹密度的影响因素，其多是对于裂纹数量不大的二维裂纹，通过人工计量的方式对裂纹数量及裂纹间距等进行统计，但对于裂纹数量较大的二维裂纹，或形态较为复杂的三维网状裂纹，就很难通过人工计量的方式进行统计。为了能够更为直观和定量地研究层厚对三种不同几何表面裂缝密度的影响，进一步探索不同几何表面上间隔破裂规律的异同，本文将借助裂隙图像分析系统(CIAS)[17-18]对达到裂缝饱和的最终裂缝形态图像进行量化统计，其示意图如图7所示。该系统可以对得到的裂缝图像(见图7(a))进行二值化处理(见图7(b))，从而对裂块进行识别(见图7(c))，并对一系列统计参数进行统计计算，我们可以根据需求选取所需的统计参数。

图7 通过CIAS系统[17]进行裂隙图像处理示意图

由于要进行三种几何表面的对比，主要统计三种几何表面均可产生的多边形网状裂隙的多边形裂块的块数N，和每个裂块的平均面积S，如图7(c)所示。并采取不同的下标进行区分，平面模型(Flat)、柱面模型(Cylinder)、球壳模型(Sphere)分别采用f、c、s作为下标。为了使分析更具实际意义，对统计的数据进行基于总和标准化的无量纲处理，即将得到的平均多边形裂块面积都除以相应的表面积，所得到的标准化平均多边形裂块面积是一个0到1的参数，故也称作归一化参数。对于表面破坏层厚度，也对其进行无量纲处理，由于表面破坏层的薄厚都是相对于基层而言的，故分析破坏层厚度对间隔破裂的影响实际上就是分析表面破坏层厚度t与基层厚度T的比值(η=t/T)对间隔破裂的影响，故以下分析中就取η为自变量，以达到无量纲分析的效果，t为5、10、15、30对应的η为0.33、0.67、1.00、2.00。

图8(a)—图8(c)分别表示了不同表层基层层厚比η与在加载比λ=Δy/Δx=1的双向拉伸作用下的平面模型、在加载比λ=Δz/Δr=1的双向载荷作用下的柱面模型和仅在径向载荷作用下的球壳模型表面多边形网状裂块数N和相应的平均裂块面积S之间的关系，每种层厚比对应的裂缝形态也在图中有所展示。结果表明，无论哪种几何表面，当层厚比η为0.33时的裂块数量都比层厚比η为2时多达10倍以上，而相应的平均裂块面积要小得多，且随着层厚比η的增大，多边形数量逐渐减少，尤其η从0.33增大到0.67的区间，减小的幅度明显，而相应的平均裂块面积越来越大。

然而，根据以上统计得到的曲线图8可以看出，虽然大体上的增减趋势相同，但还是存在一些差异，为了更为直观的观察三种几何面在不同层厚比下的裂缝统计曲线趋势的差异，将三种几何面网状裂缝统计曲线绘制在同一坐标系下，如图9所示。三条实线表示破裂层厚度对多边形裂块数的影响，由于三种几何面具有不同的尺寸，我们不对具体数值做比较，仅观察趋势发现，三条实线具有相同的趋势，随着层厚比η的增大，多边形裂块数量单调减少并逐渐趋于1。这表示随着表面破坏层相对于基层厚度达到一定值时，破坏层几乎不产生裂缝。

三条虚线表示破裂层厚度对归一化的平均多边形裂块面积的影响，可以观察到代表柱面和球面的两条虚线是近乎重合的，而板面则表现出不同的趋势，即平面模型表面的裂块面积表现为随层厚比η增大而先大幅增加，再逐渐变缓表现出收敛的趋势，而球面和圆柱面的裂块面积表现为起初缓慢增长逐渐增速变快。这种趋势的差异有可能是受平面模型有限边界的影响，相对于柱面和球面分别属于半闭合和闭合曲面，平面的边界很大程度的限制着裂块的大小。此外，可以观察到，在相同的层厚比η条件下，平面表面的归一化平均裂块面积较球面和柱面的大。可以推测在相同的层厚比η条件下，曲面比平面产生的裂缝更密，裂块更小。但这一初步的推测还存在一些不确定因素，如三种不同的几何表面的尺寸差异，尤其对于平面的有限边界来说，尺寸的大小很大程度上限制着破裂的发展。有限边界对破裂的限制及曲面的曲率对于裂纹密度的影响还需进一步探索。

图8 层厚比分别与三种几何表面多边形裂块数和归一化平均裂块面积的关系及相应的破裂形态

图9 层厚比与三种几何表面多边形裂块数和归一化平均裂块面积的关系对比

3 结 论

(1) 裂缝形态的转变取决于不同加载条件。在平面和柱面模型表面都可以通过改变不同方向的加载比实现三种裂缝形态(平行裂缝、梯状裂缝、网状裂缝)的连续转变，而在球壳模型表面，只能形成网状裂缝。在球壳模型中，径向载荷导致沿着层面的双轴同增量拉伸应力，而在圆柱模型中，径向载荷则是导致沿圆周方向的单轴拉伸应力。

(2) 表层与基层厚度比与表面裂缝密度的关系不受模型表面的几何形状的影响。即无论哪种几何表面，随着厚度比η从0.33增大到2，表面裂块数量均减少10倍以上，并逐渐趋近于1。这表示随着表面破坏层的厚度相对于基层厚度达到一定值时，破坏层几乎不产生裂缝。

(3) 推测在相同的层厚比条件下，曲面比平面产生的裂缝相对更密，形成的网状裂块相对更小。