下沉过程耦合欧拉-拉格朗日有限元法分析

2020-07-07霍知亮郎瑞卿闫澍旺

水利与建筑工程学报 2020年3期

霍知亮，郎瑞卿，闫澍旺

(1. 天津大学建筑工程学院，天津 300072; 2.天津市市政工程设计研究院，天津 300051; 3.天津市软土特性与工程环境重点实验室，天津 300384)

在进行基础或结构物下沉贯入的数值分析时，常会遇到接触处理困难、网格大变形造成的扭曲畸变等问题，引起程序收敛困难、计算失真。应用何种数值分析方法，准确的模拟下沉过程结构物和土的相互作用，已成为此领域的一个重要课题[1-2]。通常采用的拉格朗日分析方法，在模拟结构物下沉贯入等大变形分析时，网格的扭曲常会导致计算的不收敛或者引起严重的误差[3]。纯粹的欧拉分析可能导致数值扩散或者边界处的材料流动未知等问题，在此类分析中并不多见。ALE方法在一定程度上克服两者的缺点。但进行下沉贯入分析时，常常为了计算的收敛性做出一些假设、以及不能很好的模拟土体“冲剪”破坏形态等问题，影响贯入物与地基土体的相互作用机理[1]。

耦合的欧拉-拉格朗日(Coupled Eulerian - Lagrangian，CEL)方法，采用了欧拉计算方法与拉格朗日计算方法各自的特点，通过固定的欧拉网格及可以在网格中运动的材料，可有效的处理网格畸变等大变形分析中存在的解法困难，在近年的分析研究中逐渐得到应用。在海洋平台桩靴下沉分析[4-7]、桩基础沉贯分析和沉船问题[8]及其他海洋基础承载力[9]中取得了一些成果。本文通过砂土中桩的静压下沉、吸力锚的自重下沉和海底管线自沉分析三个应用实例，表明CEL方法在模拟下沉贯入问题时的适用性及其优势。其分析方法和成果可为其它类型基础结构的下沉分析提供有益参考。

1 耦合欧拉-拉格朗日(CEL)法

耦合欧拉-拉格朗日(CEL)法采用了欧拉计算方法与拉格朗日计算方法各自的特点。通常将基础或结构物模拟为拉格朗日网格，地基土体模拟为欧拉网格，通过固定的欧拉网格，材料可以在固定的网格中运动，从而可有效的处理网格畸变等大变形分析中存在的解法困难。并且，其相应的接触算法可以较好的模拟结构物与土的相互作用，得到准确的分析结果。两种有限元法中物体的变形原理如图1所示。

图1 不同有限元法中物体的变形

1.1 欧拉体积分数

在CEL有限元方法中，通过各个单元体中的欧拉体积分数(Eulerian Volume Fraction，EVF)来确定欧拉体在网格中的运动轨迹。若所建立的参考体全部填充于所建立的欧拉单元，则对应的欧拉体积分数EVF为1.0；反之，若参考体完全未填充于欧拉单元，则对应的欧拉体积分数EVF为0.0。若所建立的参考体部分填充于所建立的欧拉单元，即EVF小于1.0时，此单元中未被填充的部位被无属性的“空”占据。其基本原理如图2所示。

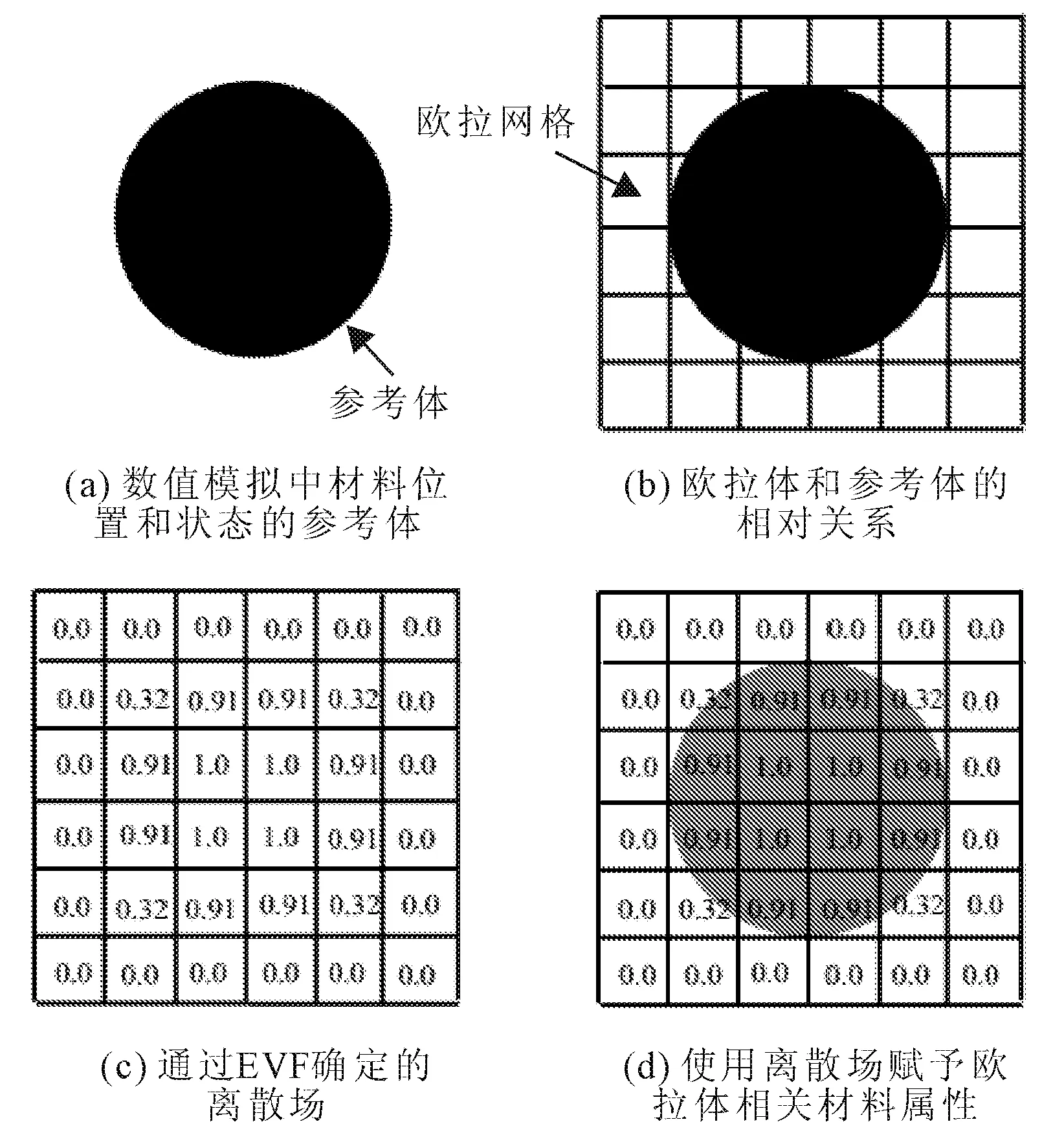
图2 通过欧拉体积分数确定材料的步骤

1.2 接触属性

在CEL有限元分析中，拉格朗日网格中的物质材料与欧拉物质材料两者的接触界面依据广义接触算法来实现，其接触算法为：

FP=kP/dP

(1)

式中：FP为接触界面上的接触力；dP为相应位置的罚位移；kP为刚度，数值的大小与接触的材料特性相关。这种接触算法可自动选定接触属性中的主面和从面，可较好的处理大变形问题中的非线性问题。

2 应用示例

2.1 砂土中桩的静压下沉

示例1应用CEL有限元法，对砂土地基中的静压桩进行贯入下沉分析。Sheng等[10]应用ALE方法并引入自动荷载施加方案和平滑接触离散技术，模拟砂土中桩的连续贯入问题。其中地基土采用摩尔-库仑准则，相应的物理力学力学指标参数：黏聚力c为1 kPa，砂土内摩擦角φ为30°，剪胀角ψ为20°。砂土重度γ为20 kN/m3。在数值分析中弹性模量E取10 MPa，泊松比υ取0.3。桩的弹性模量E=100 GPa，泊松比υ=0.3。数值计算区域为消除边界效应对计算结果的影响，模型的长和高分别取为2.4 m和4.8 m，静压桩的直径为0.8 m，桩长为3 m，根据Sheng等[10]计算模型，桩端角度为60°，摩擦系数μ取0.01，桩的贯入深度为2.5 m。

应用CEL有限元法建立三维有限元计算模型，采用上述基本计算条件。计算得出的桩贯入阻力和贯入位移的关系，经过归一化处理，得到计算结果分别如图3和图4所示。从计算结果可以看出，其计算结果和Sheng等采用ALE有限元法的计算结果相近。

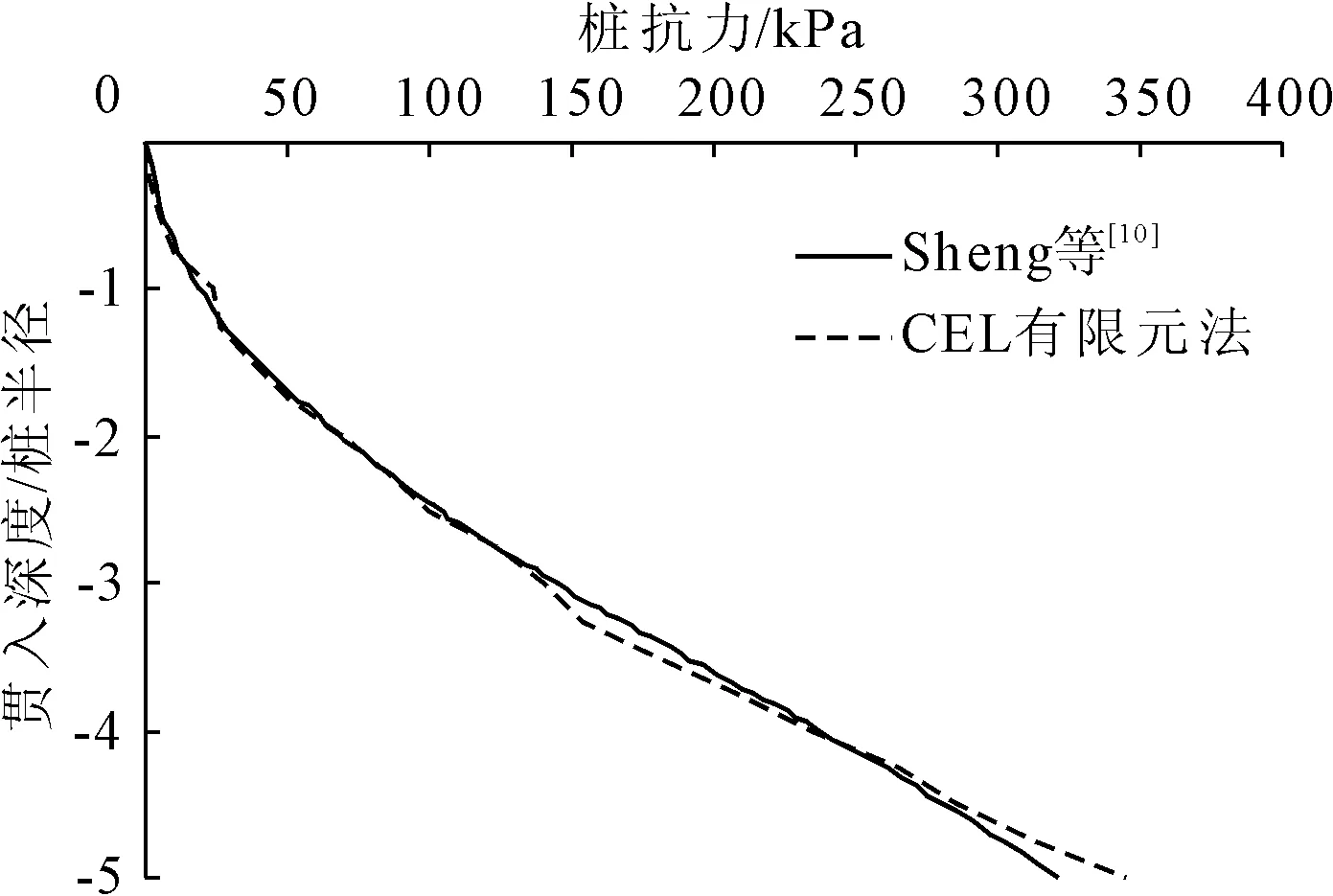
图3 桩贯入时抗力和贯入深度曲线

图4 桩贯入时土体的变形

通常，应用ALE有限元法进行基础贯入分析时，为了避免在最初贯入下沉时网格变形过大，常把桩端模拟成锥形(例如Sheng等[10]、Henke[11])，并且为了模拟连续贯入，常使用zipper-type技术，即在桩端利用极细的光滑接触刚性管，从而达到桩在贯入时与土平滑的接触，更利于计算的收敛性(例如Mabsout等[12])。但做出这样的简化，在模拟桩下沉时会对桩-土相互作用和沉桩机理分析产生影响。应用CEL有限元法无需对桩端截面进行修改，不需其他简化即可模拟桩的连续贯入。

2.2 吸力锚自重下沉

示例2应用CEL有限元法，对Luke[13]和Vásquez等[14]吸力锚自重下沉模型试验和有限元分析进行模拟，并与其结果进行比较。在Vásquez等[14]对吸力锚自重下沉有限元分析中，通过开发一种摩擦接触算法，并且应用重划分网格技术，模拟吸力锚自重下沉和负压下沉过程，计算吸力锚下沉时孔隙水压力变化以及下沉深度和土体抗力之间的关系。

在Luke[13]的模型试验中，试验槽高为1.829 m，直径1.219 m。土体为高岭土，其十字板抗剪强度su随深度线性增加。吸力锚长L=0.914 m，直径D=10.2 cm，长细比L/D=9，壁厚t=0.81 mm，裙壁与土的摩擦系数为0.16。试验具体情况和详细参数见Luke等[13，15]。应用CEL有限元法建立三维有限元计算模型，模拟吸力锚自重下沉过程，计算得出的力和下沉深度的关系曲线如图5所示。CEL有限元法计算结果在吸力锚下沉深度为0.3 m以内时，与试验值吻合较好，当下沉深度超过0.3 m时，CEL有限元法比试验值略大，但计算结果与室内试验得出的力和下沉深度关系曲线趋势基本相同。采用CEL有限元法无需开发摩擦接触算法和重划分网格技术，其应用更为简便。

需要指出，显示动力计算方法与普通静态应力/位移分析相比，由于采用中心差分方法进行求解，在计算过程中对时间积分，其计算结果可能会产生波动或离散性(如图5所示)。对于此种情况，分析者可根据计算结果和分析需要，采用例如Butterworth或者其它滤波函数[16]对曲线进行滤波处理。

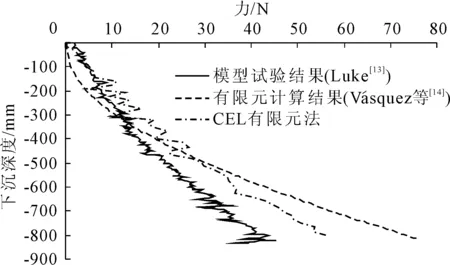
图5 吸力锚自重下沉时力和下沉深度曲线

2.3 海底管线自沉分析

示例3对海底管线自沉进行分析。海底管线作为传输石油、天然气的介质和通道，是海洋油气开发的重要组成部分。在远离海岸的深海区域，海底管线通常直接铺设在海床上，无需特意沟埋等工程保护措施，通过自沉或配重自沉下沉至海床内一定深度。通常，单孔的海底管线在铺设过程中，其下沉深度约为0.1倍～0.5倍的海管直径[17]。海管的自沉深度是分析海底管线屈曲等稳定性的一个重要参数。

对于海管下沉的理论分析，国内外许多学者依据承载力基本原理，结合管道基底特点进行了修正，提出了软土地基海底管线下沉时竖向抗力的理论解[18-22]，其计算公式为：

(2)

(3)

式中：V为管线承受的竖向荷载，kN/m；su0为不同深度处地基土不排水抗剪强度，kPa；Nc为承载力系数；As为管线下沉时的截面积，m2；fb为浮力系数；D为管线的外径，m。根据Merifield等[22]、Randolph等[23]的研究成果，因管线下沉时地基土体将发生隆起现象，建议浮力系数fb宜取1.5。管线下沉示意图如图6所示，其计算公式为：

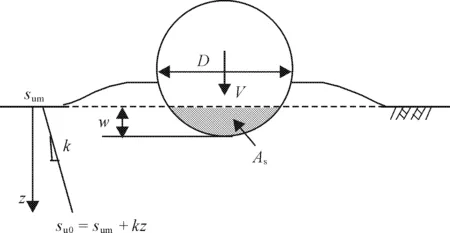
图6 管线下沉示意图

(4)

(5)

Nc承载力系数与管线的直径和下沉深度有关，根据现有的研究成果，其表达式为幂函数的形式[18,20,22]，如下所示：

(6)

式中：w为管线的下沉深度；a、b为拟合系数，其数值的大小和接触面的粗糙程度、kD/sum的大小有关。系数a和b的取值见Aubeny等[20]。

采用CEL分析方法对饱和软黏土地基中海管下沉进行模拟分析。取管线直径D=0.8 m，模型区域为10D×8D，考虑安装沉放和地基土的不排水特性，土体采用Tresca屈服准则，土体重度γ′取6.5 kN/m3，弹性模量和不排水抗剪强度的比值为500，即E/su=500，泊松比为0.49。地基土考虑了强度与埋深的线性关系，具体如图6所示，其中地表土体sum取2.3 kPa，线性增加比例k取3.6 kPa/m。海管和地基土之间的接触分别模拟为光滑和粗糙情况。

对于此类情况，Chatterjee等[24]采用考虑了大变形的RITSS方法进行模拟研究，此外，Tian等[25]采用二次开发程序，并结合大型商用软件ABAQUS的“网格-网格的映射方法”，计算分析了海管自沉时土体节点的应力和变形，并进行网格重划分，处理海管下沉过程中的大变形的问题。采用CEL计算方法，并与式(2)的计算结果进行分析对比，结果如图7所示。从计算结果可以看出，CEL计算结果与式(2)结果较为接近，并且Chatterjee等[24]和Tian等[25]的计算结果位于光滑界面和粗糙界面所得的模拟结果之间。通过分析可看出，CEL方法可有效模拟海底管线大变形问题，所得的计算结果对于此类问题有较好的适用性。