单圈图的原子键连通性指数的上界

周后卿

(邵阳学院 理学院,湖南 邵阳,422000)

设G=(V,E)是具有顶点n的简单分子图,记顶点集V={1,2,…，n},边集为E(G)。基于图的分子结构描述符(通常称为拓扑指数)是刻画分子物理和化学性质、设计药理活性化合物、识别环境有害物质等方面的有用工具[1]。分子描述符在QSPR/QSAR研究中有着广泛的应用,譬如20世纪70年代中期由RANDIC引进的、著名的、广泛使用的连通指数χ,用这个指数来反映分子的分支[2]。关于分支的一些新结果可以在文献[3-5]和其中引用的参考文献中找到。ESTRADA等[6]于1998年提出了一个新的指数,即现在称为原子键连通性指数的ABC指数。定义分子图的ABC指数

本文讨论简单连通图、单圈图的ABC指数的上界问题。

1 几个已知结论及引理

首先介绍几个概念。单圈图是边数等于顶点数的简单连通图,记n阶单圈图的集合为Un。具有4个顶点的单圈图G，如图1所示。

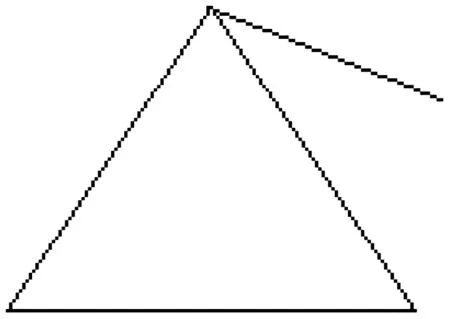
图1 具有4个顶点的单圈图GFig.1 The unicyclic graph G with 4 vertices

分子图的第一类Zagreb指数、第二类Zagreb指数分别用M1和M2表示,记作:

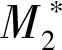
也可表示成

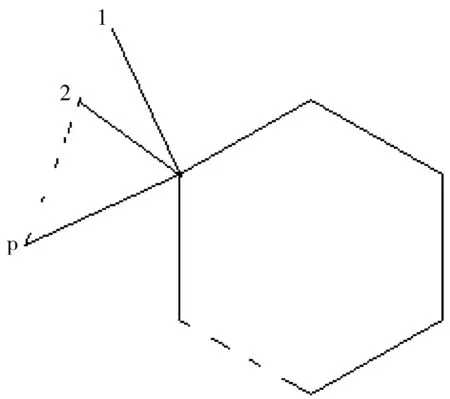
图2 具有n个顶点、p条悬挂边的单圈图G1Fig.2 The unicyclic graphG1with n vertices、p pandent edges

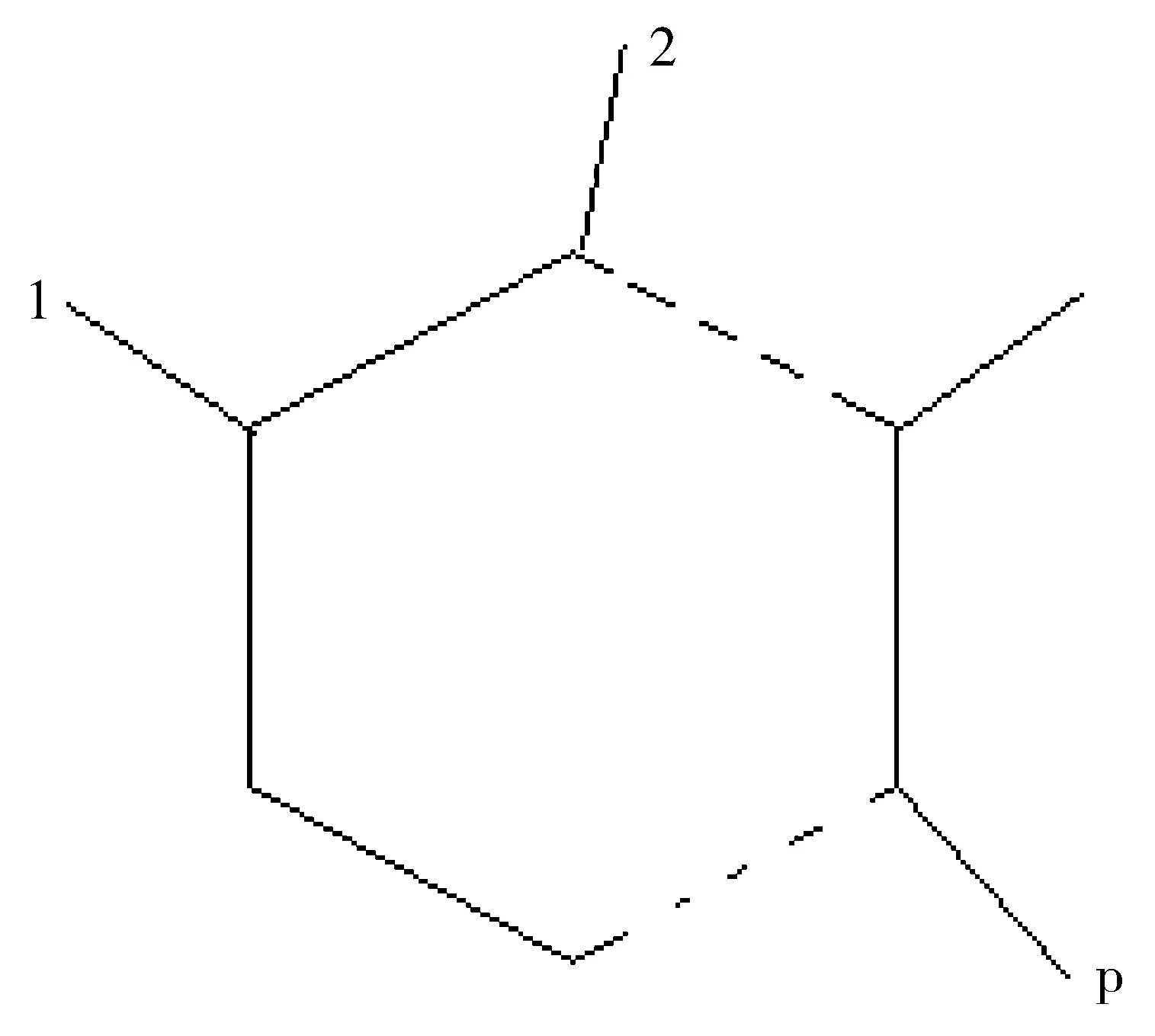
图3 具有n个顶点、p条悬挂边的单圈图G2Fig.3 The unicyclic graphG2with n vertices、p pandent edges

对于图3中的G2,有

M1=p(3+1)+(p-1)(3+3)+2(3+2)+(n-2p-1)(2+2)=2p+4n≤p(p+1)+4n

说明图2中M1比图3中的M1大。

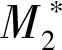
下面给出几个已知结论。

DAS等在文献[9]中给出了ABC指数的一个上界。

定理1若G是具有n个顶点,m条边,p个悬挂顶点的简单连通图,最大顶点度为Δ,最小非悬挂顶点度为δ1，则

当且仅当G同构一个半正则二部图，等式成立。

在文献[10]中,DAS证明了下列结论。

定理2若G是具有n个顶点,m条边,p个悬挂顶点的简单连通图,最大顶点度为Δ,最小非悬挂顶点度为δ1。则

当且仅当G同构一个半正则二部图，等式成立。

在文献[8]中,FURTULA等人给出了树的界,得到下列定理。

定理3设T是一个顶点为n的化学树(所谓化学树，是指顶点的度小于等于4的树),则

现在证明简单连通图的ABC指数的上界。

为了证明定理,需要下述引理。

引理1[11]若G是具有n个顶点,m条边,最大顶点度为Δ的简单连通图。则

2 主要结论

现在证明本文的第一个结论。

定理4若G是具有n个顶点,p(p≥1)个悬挂顶点,最大顶点度为Δ,最小非悬挂顶点度为δ1的单圈图，则

证明显然,悬挂顶点个数p≥1,最小非悬挂顶点度δ1>1,所以有-p(δ1-1)<0。

由于G是具有n个顶点,p个悬挂顶点的单圈图,所以,m=n,且

M1-2m-p(δ1-1)≤Δ2+2n-3p-4,

现举例说明定理的可行性。设单圈图U5如图4所示,按照ABC指数的定义计算,可得到ABC(U5)=3.85。由于n=5,Δ=4,p=2,按定理4计算有ABC(U5)≤4.852,显然3.85<4.852,定理4成立。

图4 具有5个顶点的单圈图U5Fig.4 The unicyclic graph U5 with 5 vertices

定理5若G是具有n个顶点,p(p≥1)个悬挂点,最大顶点度为Δ的单圈图,则

证明由定理条件可知,p≥1,δ1>1,从而-p(δ1-1)<0,

对于单圈图有,n-2≤Δ≤n-1,所以,1≤n-Δ≤2。

又m=n,根据引理1,

于是有

仍以上述单圈图为例。利用定理5计算,得

ABC(U5)<5.102。显然,3.85<5.102,说明定理5成立。