陶瓷/钛合金靶抗圆柱体弹侵彻的仿真研究

张元豪,程忠庆,侯海量

(1.海军工程大学 舰船与海洋学院,湖北 武汉 430033;2.海军勤务学院,天津 300450)

全世界范围内反舰导弹正不断发展,半穿甲反舰导弹侵入船体内部爆炸,产生的高速破片会对舰船重要舱室及人员造成严重影响,所以舰船舱壁的抗穿甲问题引起了广泛的关注。为提高舰船的生命力,舰船装甲从单一的均质金属装甲逐步发展为复合装甲。

陶瓷装甲具有低密度、高硬度、高抗压强度等特点,适合用作复合装甲的迎弹面板,国外针对将陶瓷作为舰艇、坦克等大型战斗设施的主体防弹材料已有大量的研究[1-3]。但是陶瓷由于自身的塑性差、断裂强度低,不能单独用作防护装甲,因此需要背板刚性支撑。目前采用的陶瓷复合装甲一般采用金属材料作为背板,陶瓷面板用于碎裂钝化破片[4-5],金属背板用于吸收破片动能。

张晓晴[6]通过弹体撞击陶瓷/金属复合靶板实验及理论分析模型,得到了侵彻动态过程及相关规律。王晓强等[7]通过实验研究了10 g破片模拟弹侵彻不同厚度配比的陶瓷/船用钢靶板的弹道极限速度,得到了弹道极限速度随陶瓷厚度和船用钢厚度变化的经验公式。迟润强等[8]利用有限元软件对氧化铝陶瓷/铝合金复合装甲的防护性能与弹靶尺寸的关系进行了研究,建立了弹道极限速度的经验公式。孙杭其[9]讨论了陶瓷/铝合金复合装甲的优化设计问题,对其厚度配比进行优化。匡格平[10]则采用数值模拟方法研究了陶瓷/钛合金结构下,弹靶尺寸对剩余速度的影响以及弹丸初速度对侵深的影响,得出了经验公式。

从研究现状发现,目前针对陶瓷/金属靶板的研究大多局限于陶瓷/钢靶板,对于陶瓷/钛合金靶板的研究鲜有报导,而钛合金因其优异的耐腐蚀、耐高温性能适合用于舰用复合装甲的背板[11-15]。

本文利用有限元分析软件ANSYS/LS-DYNA研究了7.5 g圆柱体弹侵彻不同厚度配比的陶瓷/钛合金靶板的弹道极限速度及靶板的破坏模式,通过分析得到了弹道极限速度随陶瓷厚度和钛合金厚度变化的经验公式,探讨了陶瓷和钛合金厚度配比对结构抗弹性能的影响规律。

1 有限元模拟

1.1 模型建立

利用有限元软件ANSYS/LS-DYNA,对高速圆柱体弹侵彻陶瓷/钛合金结构进行数值模拟研究。弹体选用长度15 mm,直径9 mm的圆柱体弹,结构中陶瓷平面尺寸为100 mm×100 mm,钛合金板平面尺寸为300 mm×300 mm。弹体、陶瓷以及钛合金板均采用8节点的Solid 164三维实体单元,采用Lagrange网格建模。弹体沿长度方向划分为15个网格,直径方向划分为12个网格;陶瓷和钛合金板沿厚度方向按每毫米1层均匀划分,面内网格在侵彻区加密,向四周稀疏过渡。数值模型采用cm-g-μs单位制。有限元模型(4 mm陶瓷+4 mm钛合金)如图1、图2所示。

图1 有限元整体模型

图2 有限元模型剖面图

弹体材料为35CrMnSiA 低合金超高强度钢，采用* MAT_PLASTIC_KINEMATIC 双线性弹塑性本构模型，模型应变率效应由Cowper-Symonds 模型描述，材料参数如表1 所示。表中，ρ为密度;μ为泊松比;σy为静态屈服强度;E为弹性模量，Eh为硬化模量;D和N为常数，对于低碳钢，通常取D= 40s-1，N= 5。

表1 弹体钢的材料模型参数

SiC陶瓷采用Johnson-Holmquist_ceramics材料模型和Gruneisen状态方程来描述,材料参数如表2所示。表中,G为剪切模量;A为无损标准强度参数,B为断裂标准强度参数;c为应变率系数;m为断裂强度指数,n为无损强度指数;D1为第一断裂参数,D2为第二断裂参数;K1,K2,K3为常数。

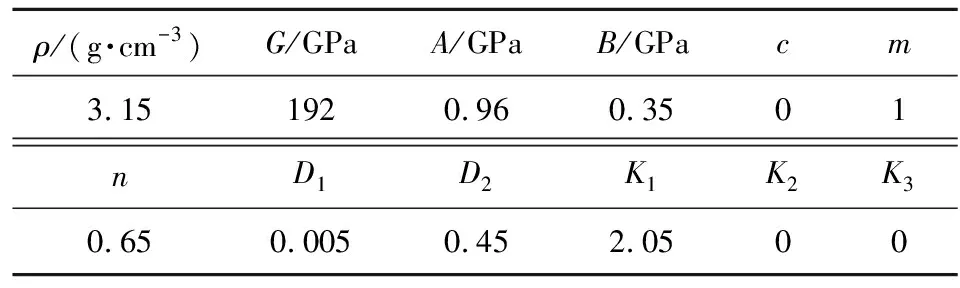
表2 SiC陶瓷的材料参数

钛合金采用Johnson-Cook材料模型[16]和Gruneisen状态方程来描述,材料参数如表3所示。表中,A1为静态屈服强度;B1为应变硬化模量;n1为应变硬化指数;m1为热软化指数;Tm为材料的熔点,T0为参考温度(取室温);D1～D5为常数。

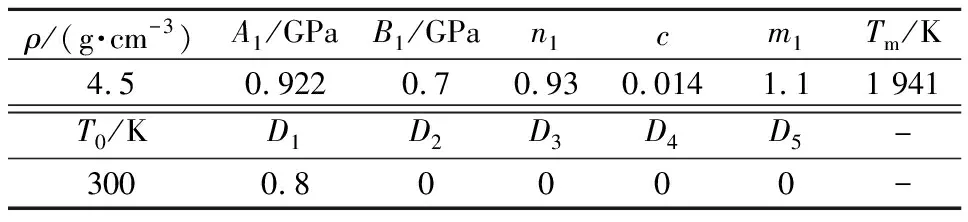
表3 钛合金材料参数

1.2 算法验证

文献[17]开展了7.62 mm及12.7 mm穿甲弹侵彻陶瓷/钛合金结构的试验,通过以上材料模型建立相应的数值仿真,与试验结果进行了对比,如表4所示。表中,C表示陶瓷,T表示钛合金,字母前数字表示厚度,如10C/3T表示10 mm陶瓷+3 mm钛合金结构。由表4可以看出,数值计算结果得到的钛合金板穿深与试验结果的误差均小于10%,认为1.1节中材料模型较为合理。

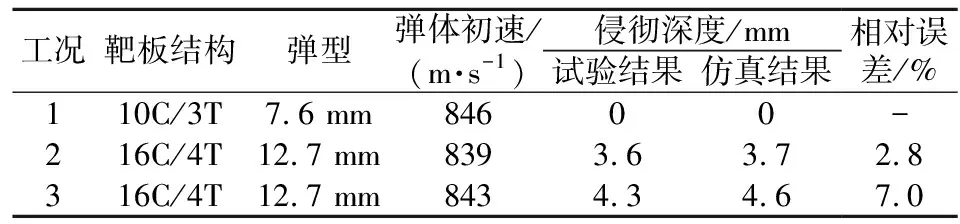
表4 数值计算结果与试验结果对比

2 数值计算结果与分析

2.1 陶瓷和钛合金厚度变化对结构破坏变形的影响

为研究靶板弹道极限速度及破坏模式随陶瓷厚度和钛合金厚度的变化关系,针对靶板结构I:3mmSiC陶瓷+钛合金,钛合金厚度dT分别取3 mm,4 mm;结构Ⅱ:4 mmSiC陶瓷+钛合金,dT分别取2 mm,4 mm,6 mm,8 mm;结构Ⅲ:5 mmSiC陶瓷+钛合金,dT取4 mm,5 mm,通过数值仿真对以上8种工况进行计算,得到了不同靶板结构下的弹道极限速度v50及弹道极限速度附近结构破坏后的变形情况,具体结果如表5所示。图3为工况2、工况4、工况5中靶板的破坏形貌图。

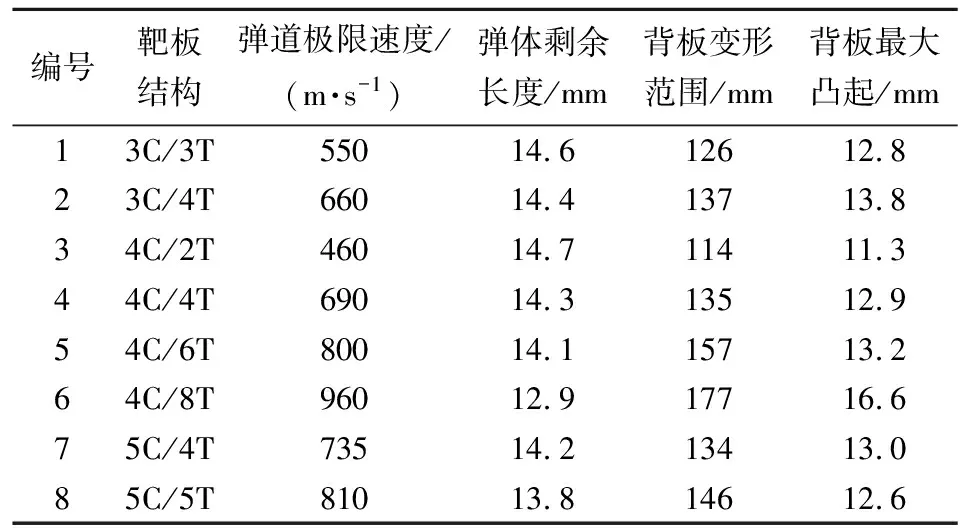
表5 不同结构在弹道极限速度侵彻下的数值计算结果

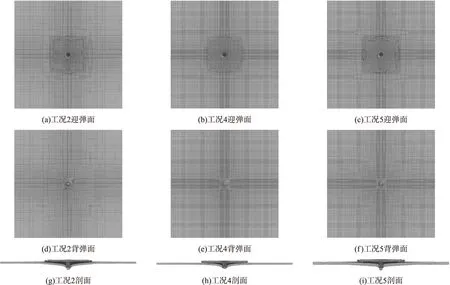
图3 靶板破坏形貌

结合表5、图3发现,当弹体速度接近弹道极限速度时,陶瓷/钛合金结构的破坏变形程度基本随着结构厚度增加而增大,并且弹道极限速度越大,靶板变形程度越大。进一步分析表5,对比工况2、工况4、工况7及工况3、工况4、工况5、工况6可以看出,增加钛合金厚度对弹体侵蚀程度及靶板变形程度产生的影响大于增加陶瓷厚度。

观察图3中靶板迎弹面破坏形貌可知,由于陶瓷为非均匀性材料,弹体撞击面板后极易在微孔洞处产生微裂纹,并在拉伸波作用下聚合扩展,最终使陶瓷面板断裂失效,陶瓷破口尺寸大于弹体直径,且陶瓷厚度越薄,弹体速度越高,陶瓷面板碎裂程度越严重;观察靶板背弹面及剖面破坏形貌可知,当弹体速度接近弹道极限速度,钛合金背板背弹面的破坏形貌呈现隆起-蝶形变形并伴随细微裂纹,同时弹道极限速度越大,钛合金靶板变形程度越大。

2.2 弹道极限速度随陶瓷和钛合金厚度的变化关系

表5给出了不同厚度下陶瓷/钛合金结构的弹道极限速度,对比3C/4T,4C/4T,5C/4T结构发现,在dT保持不变的情况下,陶瓷/钛合金结构的弹道极限速度随陶瓷厚度dC的增加基本呈线性增长的变化趋势,通过线性拟合,得到弹道极限速度v50随陶瓷厚度dC的变化公式如式(1);对比4C/2T,4C/4T,4C/6T,4C/8T结构发现,在dC保持不变的情况下,陶瓷/钛合金结构的弹道极限速度随dT的增加同样呈线性增长的变化趋势,通过线性拟合,得到弹道极限速度v50随钛合金厚度dT的变化公式:

v50=37.5dC+545

(1)

v50=80.5dT+325

(2)

通过式(1)、式(2)可分别计算得到不同陶瓷厚度与4 mm钛合金板组合结构、4 mm陶瓷与不同厚度钛合金板组合结构的弹道极限速度。图4、图5分别为弹道极限速度随陶瓷厚度、钛合金厚度变化的拟合曲线,对比仿真结果与拟合结果可知,最大相对误差的绝对值为6.9%,因此用式(1)、式(2)来计算陶瓷厚度、钛合金厚度变化引起的弹道极限速度变化是可靠的。

由图4、图5显示的弹道极限速度随靶板厚度变化的规律并结合式(1)、式(2)对于弹道极限速度的预测公式,可知陶瓷与钛合金厚度变化对弹道极限速度的影响有所差别:式(1)表示在钛合金厚度保持不变的情况下,增加1 mm陶瓷,结构的弹道极限速度随之增加37.5 m/s;式(2)表示在陶瓷厚度保持不变的情况下,增加1 mm钛合金,结构的弹道极限速度随之增加80.5 m/s。因此当陶瓷和钛合金同时发生厚度变化时,弹道极限速度随之变化的公式表达为

v50=37.5dC+80.5dT+P

(3)

式中:P根据仿真结果拟合得到,P=161.3。

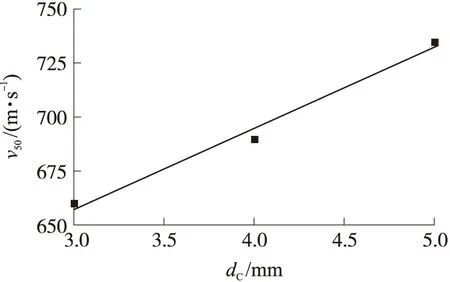
图4 弹道极限速度随陶瓷厚度的变化拟合曲线

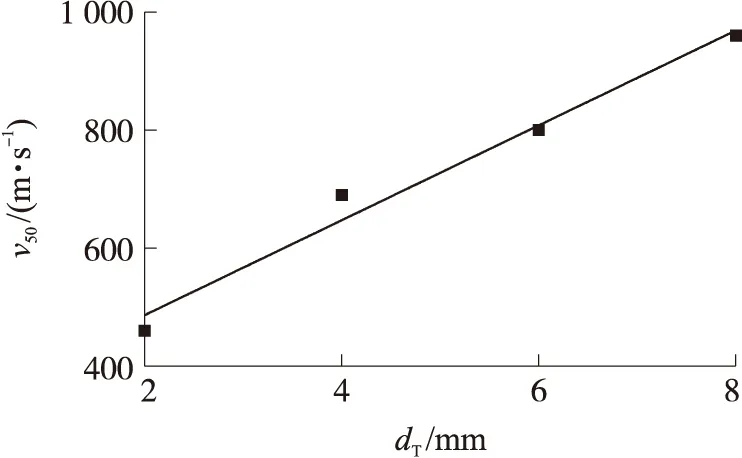
图5 弹道极限速度随钛合金厚度的变化拟合曲线

综上所述,得到7.5 g圆柱体弹侵彻下,任意厚度陶瓷/钛合金结构的弹道极限速度计算公式:

v50=37.5dC+80.5dT+161.3

(4)

为验证拟合公式的准确性,对靶板结构3C/5T,3C/6T,4C/5T,4C/7T,5C/3T,5C/6T进行数值模拟计算,对比了6种结构在仿真计算下及拟合公式计算下的弹道极限速度,结果如表6所示。

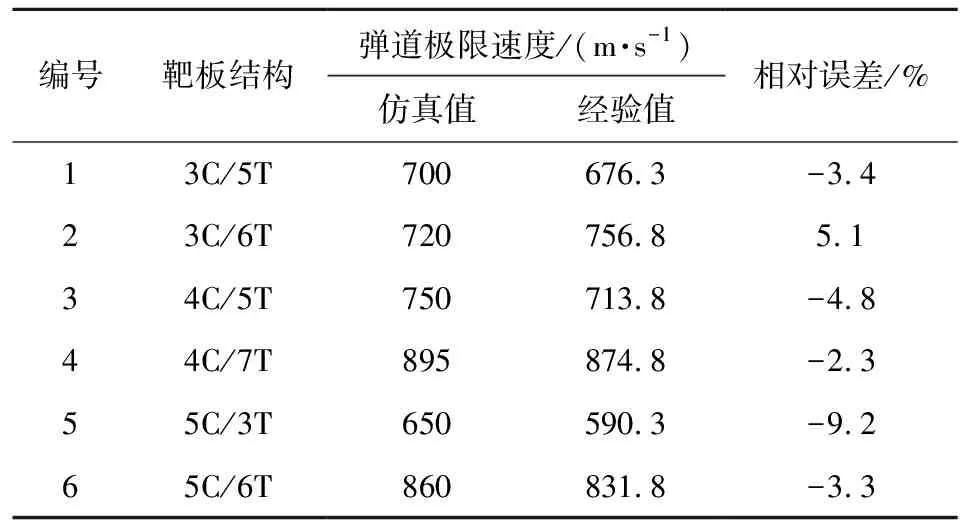
表6 数值计算结果与拟合公式计算结果的对比

表6中以仿真结果为基准,拟合公式得到的弹道极限速度与仿真值的相对误差绝对值均小于10%,因此该拟合公式能合理预测陶瓷/钛合金结构的弹道极限速度。

2.3 陶瓷/钛合金厚度比对结构抗侵彻性能的影响

陶瓷/钛合金厚度比变化会影响弹体侵蚀程度、钛合金靶板的变形程度,进而影响陶瓷/钛合金结构的抗弹性能。为研究陶瓷/钛合金厚度比对结构抗侵彻性能的影响规律,定义弹体初速为1 000 m/s,选取陶瓷厚度为3 mm,4 mm,5 mm,6 mm,钛合金厚度由1 mm,依次增加1 mm,直至7 mm,通过对以上工况进行数值模拟计算,得到不同靶板结构下弹体的剩余速度及单位面密度吸能,具体结果如表7所示。

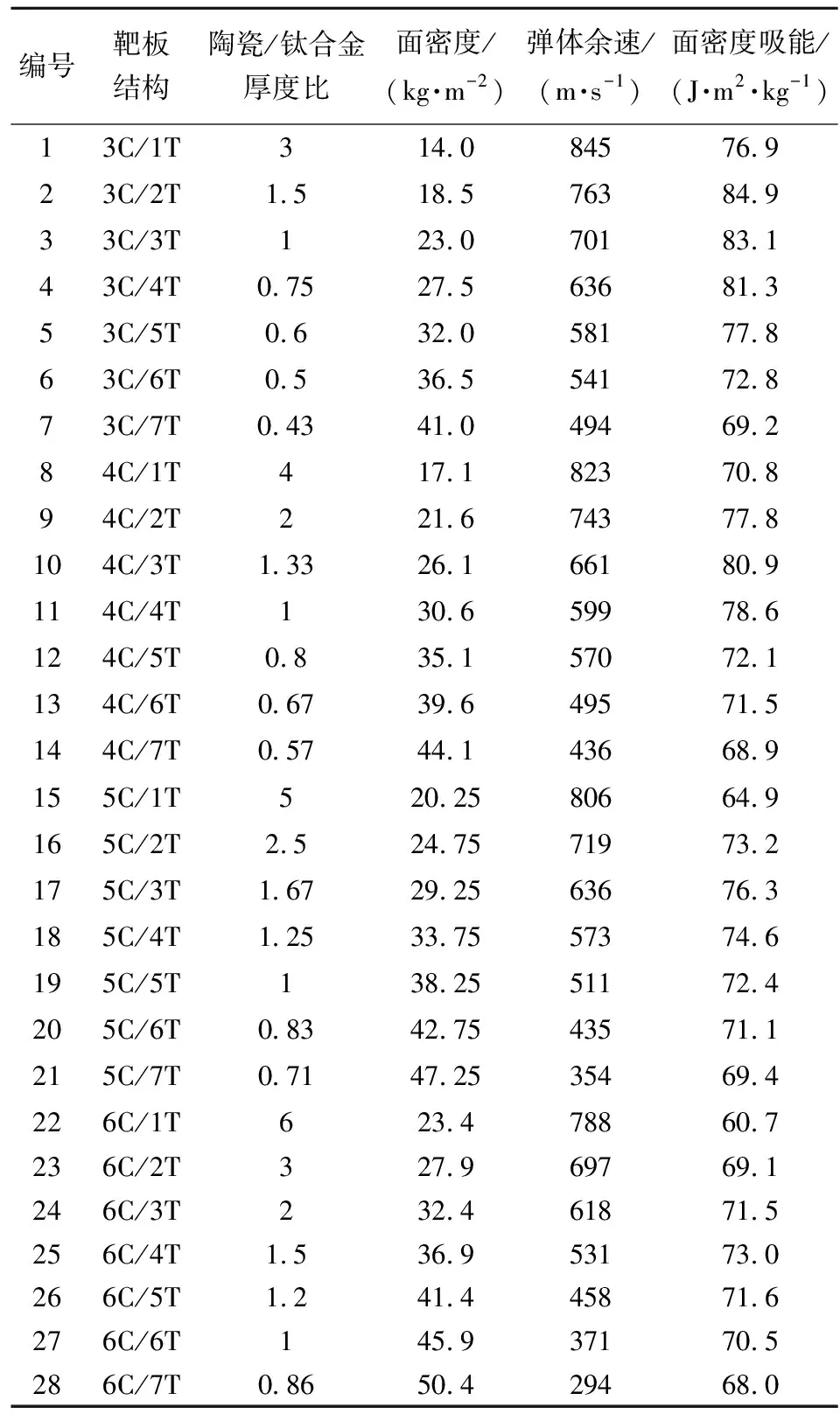
表7 不同陶瓷/钛合金厚度比时结构抗侵彻数值计算结果

根据表7中的数据绘制靶板单位面密度吸能EA随陶瓷/钛合金厚度比的变化曲线,如图6所示。观察图6发现,陶瓷/钛合金结构的单位面密度吸能随陶瓷/钛合金厚度比的增大先增大后减小;在各陶瓷厚度下,结构单位面密度吸能分别在陶瓷/钛合金厚度比为1.5,1.33,1.67,1.5时出现峰值。因此认为当陶瓷/钛合金厚度比在1～2之间时,结构抗弹性能较好。

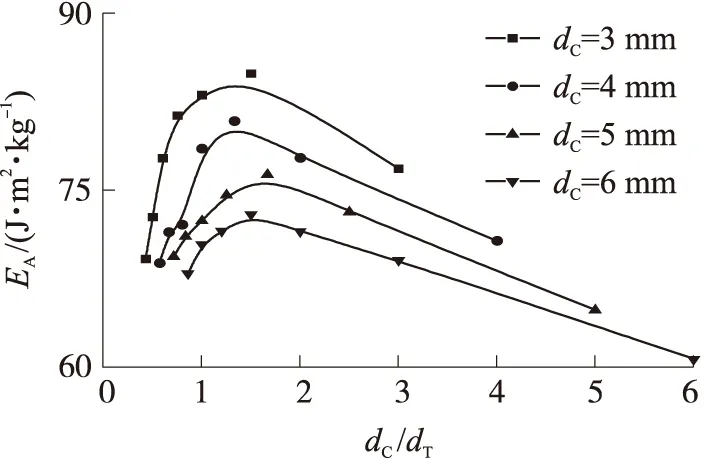
图6 单位面密度吸能随陶瓷/钛合金厚度比的变化曲线

由图6可知,当陶瓷/钛合金厚度比较小时,结构的单位面密度吸能随厚度比的增大而增大,这是由于陶瓷厚度太小,无法充分碎裂、侵蚀弹体,弹体破坏吸能较小,分散冲击载荷作用较弱,且钛合金背板受撞击时弹速仍然较高,背板无法充分变形,导致吸能也较小。随着厚度比的增大,单位面密度吸能达到一个极大值,此后单位面密度吸能随厚度比的增大而减小,原因是背板厚度太小,无法对陶瓷面板形成有力支撑,陶瓷过早失效同样无法充分碎裂弹体。

3 结论

本文利用有限元分析软件ANSYS/LS-DYNA进行数值模拟,研究了7.5 g圆柱体弹侵彻不同厚度配比的陶瓷/钛合金靶板的弹道极限速度及靶板的破坏模式,探讨了陶瓷和钛合金厚度配比对结构抗弹性能的影响规律,得到如下主要结论:

①陶瓷/钛合金结构的破坏变形程度基本随着结构弹道极限速度的增大而增大,并且增加钛合金厚度对弹体侵蚀程度及靶板变形程度产生的影响大于增加陶瓷厚度。

②得到了7.5 g圆柱体弹侵彻任意厚度陶瓷/钛合金靶板的弹道极限速度拟合公式,将仿真计算结果与拟合公式计算结果进行对比,认为该拟合公式能合理预测陶瓷/钛合金结构的弹道极限速度。

③结构的单位面密度吸能基本随陶瓷/钛合金厚度比的增大呈先增大后减小的趋势,当陶瓷/钛合金厚度比在1～2之间时,结构抗弹性能较好。

本文得到的结论为舰船舷侧防弹所需要的陶瓷和钛合金厚度提供了参考,下一步将继续开展相关试验研究。