航空末敏弹子弹地面散布研究

马宗成,陈丹强,李国帅,钟咏兵,肖树臣

(空军航空大学 航空作战勤务学院,吉林 长春 130000)

航空末敏子母弹地面散布的形状、大小和均匀程度直接影响子母弹对目标的杀伤效果[1]。与传统子母弹相比,由于航空末敏弹的弹道涉及母弹飞行过程、减速过程和稳态扫描过程3个阶段,减速和稳态扫描过程又包含伞-弹双体运动,因此航空末敏子母弹全弹道数学模型复杂,导致缺少对航空末敏子母弹地面散布问题的研究。文献[2-3]建立了传统子母弹抛撒段弹道模型,分析了无控子弹运动规律和散布情况;文献[4-6]分析了末敏弹稳态阶段伞-弹系统空间运动的运动规律;文献[1,7]采用蒙特卡罗法和数学建模的方法对破片杀伤子母弹的地面散布问题展开了研究,不涉及末敏弹的减速和稳态扫描过程;文献[8]采用上下界估计方法,对航空末敏弹的地面散布问题做了初步探讨。

本文针对航空末敏子母弹地面散布问题,采用欧拉方法建立了母弹飞行阶段的刚体六自由度动力学模型;将子弹减速阶段和子弹稳态扫描阶段的伞-弹系统简化为双刚体,根据其物理特性,将减速阶段简化为球铰链连接,将稳态扫描阶段简化为柱铰链连接,采用拉格朗日多刚体建模方法,分别建立了三维空间的减速阶段的双刚体球铰9自由度模型和稳态扫描阶段的双刚体柱铰7自由度模型。更进一步,将减速伞和旋转伞的开伞充气的衔接过程简化为匀速运动过程,建立了航空末敏弹全过程的外弹道数学模型;按照传统的抛撒方式设计了基本的航空末敏弹构型,仿真分析了水平投弹速度和抛撒速度对一层子弹地面散布的影响。本文所设计的构型和建立的全弹道模型为航空末敏弹的设计和使用提供了借鉴和依据。

1 模型构建

1.1 弹体结构和抛撒过程

本文设定母弹弹体内部装载3层且每层包含4枚的子弹,抛撒装置位于母弹弹轴处,排列方式示意图如图1所示。到达预定抛撒高度后,切割母弹的蒙皮,抛撒装置作用,将末敏子弹抛射出去。末敏子弹散开的同时,立即打开减速降落伞进入减速阶段。减速到预定速度后,抛掉减速降落伞并打开旋转降落伞,进入稳态扫描阶段,实现对地面目标的螺旋线扫描,如图2所示。

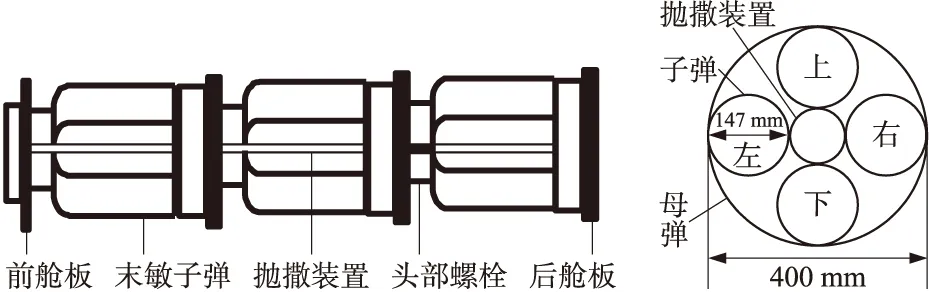
图1 弹体结构

1.2 拉格朗日多刚体建模方法简介

拉格朗日多刚体建模方法可以忽略系统之间的相互约束,仅需要求解方程中各项的表达式,进而代入第二类拉格朗日方程便可以建立多刚体动力学模型,且建立的模型是混合的微分-代数方程组,便于计算机仿真计算,第二类拉格朗日方程表达式为[9]

(1)

式中:T为多个刚体的动能,包括速度项和转动所产生的动能;qk为假设的广义坐标;Qk为相应广义坐标的广义力;k为多个刚体独立的自由度个数;n为组成质点系的个数;s为完整约束。对于由n个质点组成且具有s个完整约束的理想约束系统,建立的模型的自由度为3n-s。

图2 抛撒过程

对减速过程和稳态过程的伞-弹系统作如下假设:

①下降过程中减速伞和旋转伞保持轴对称状态,视为刚体,将末敏子弹作为另一个刚体处理,伞-弹系统视为双刚体;

②根据物理连接关系,减速过程减速伞-末敏子弹之间的连接机构简化为球铰连接,稳态阶段旋转伞-末敏子弹间连接机构简化为柱铰连接,忽略铰处产生的摩擦力。

1.3 母弹飞行过程建模

参考文献[10-11],采用欧拉方法,本文建立的母弹飞行过程的六自由度数学模型如下:

(2)

(3)

式(2)为母弹的动力学方程,式(3)为母弹的运动学方程。式中:x,y,z为惯性系下质心位置;m,J分别为母弹质量和转动惯量;v为质心速度;θ,γv分别为弹道倾角和弹道偏角;ω为角速度;ϑ,ψ,γ为欧拉角;F,M分别为弹体受到的空气作用力和力矩。

1.4 减速过程弹伞系统建模

本文选取弹伞连接点O在地面惯性坐标系Oxyz的位置参数(x0p,y0p,z0p)以及伞的空间姿态参数(ϑp,ψp,γp)和弹的空间姿态参数(ϑb,ψb,γb)作为独立变量,建立减速伞-末敏子弹双刚体球铰三维空间的9自由度数学模型。减速伞和末敏子弹组成的伞-弹系统如图3所示,图中,O1x1y1z1和O2x1y1z1分别是以伞体质心为原点和弹体质心为原点的平移坐标系。

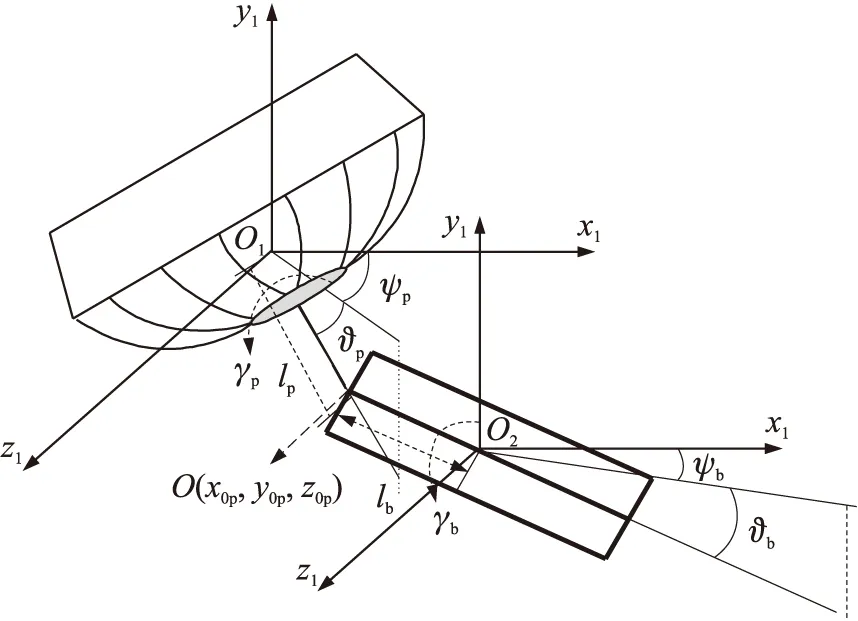
图3 减速阶段伞-弹系统示意图

根据物理连接关系,减速伞质心在Oxyz中的位置可表示为

(4)

末敏子弹在Oxyz中的位置可表示为

(5)

将式(4)和式(5)中的减速伞和末敏子弹的空间位置对时间求导数,可以求得减速伞和末敏子弹的质心速度。减速伞的质心速度可表示为

(6)

末敏子弹的质心速度可表示为

(7)

式中:ϑ′p和ψ′p为伞体的欧拉角对应的导数。

通过减速伞和末敏子弹的空间姿态角的角度变化率,可以求得减速伞和末敏子弹的角速度。可得减速伞的角速度为

(8)

末敏子弹的角速度为

(9)

因而,减速伞的动能可以表示为

(10)

末敏子弹的动能可以表示为

(11)

伞-弹系统的动能可以表示为

Tj=Tp+Tb

(12)

将式(12)代入式(1),定义广义坐标的一阶导数变量和二阶导数变量,运用MATLAB软件进行公式推导,得到伞-弹系统减速阶段三维空间9自由度数学模型为

(13)

式中:A,B,C为系数矩阵,Q为广义力项,O为零矩阵。

1.5 稳态过程伞-弹系统建模

选取旋转伞-末敏子弹系统的连接点O的空间位置(x0s,y0s,z0s)、旋转伞的空间姿态角(ϑs,ψs,γs)以及末敏子弹的弹体坐标系相对于旋转伞的伞体坐标系转动的角度θ(逆时针为正)作为广义坐标,即q=(x0sy0sz0sϑsψsγsθs)。稳态阶段的伞-弹系统的结构如图4所示。

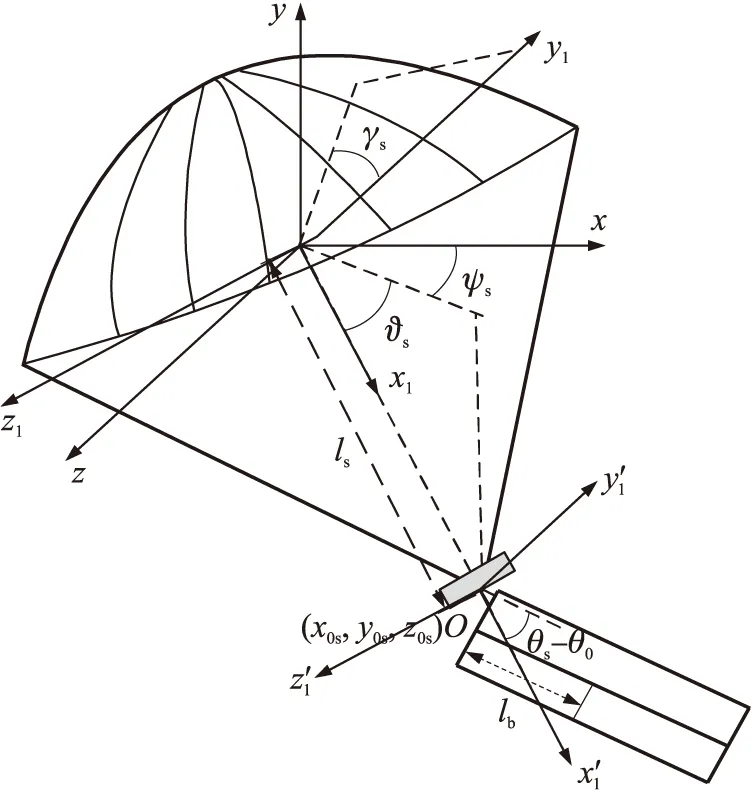
图4 稳态阶段旋转伞-末敏子弹系统示意图

将伞体坐标系平移到O点,得到伞盘坐标系Ox′1y′1z′1,则由结构参数和连接关系可以得到,伞刚体的质心在此坐标系中的位置可以表示为(-ls,0,0),弹刚体的质心在此坐标系中的位置可表示为(lbcosθr,lbsinθr,0),θr=θs-θ0,θ0为静态悬挂角。

通过坐标系转换关系,可得到伞刚体的质心在地面惯性坐标系中的坐标为

(14)

将式(14)的两边对时间求导数,可得到伞刚体的质心速度为

(15)

弹刚体的质心在地面坐标系中可表示为

(16)

将式(16)两边对时间求导数,可得弹刚体的质心速度表达式为

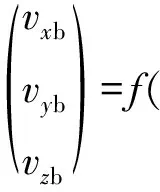
(17)

地面坐标系经过3次旋转(γs,ϑs,ψs)可以得到伞体坐标系,因此伞刚体的角速度可表示为

(18)

地面坐标系经过4次旋转(γs,ϑs,ψs,θs)可以得到弹体坐标系,因此弹体的角速度可表示为

(19)

伞刚体的动能可表示为

(20)

弹刚体的动能可表示为

(21)

稳态阶段伞-弹系统的动能可表示为

Tw=Ts+Tb

(22)

将式(21)代入式(1)中,可以得到弹伞系统在稳态扫描阶段的数学模型的表达式为

(23)

式中:A1,B1,C1为系数矩阵;Q1为广义力项。

1.6 衔接过程的假设

①抛撒点末敏子弹速度的计算。由于抛撒持续时间很短,本文假设抛撒点子弹脱离母弹后的速度为[12]v2=v0+v1。式中:v0为母弹飞行的速度矢量;v1为母弹抛撒子弹的相对速度矢量。

②开伞过程。减速伞和旋转伞开伞过程持续时间短[12],经过大约0.5 s便可以充满,因此本文将开伞充气过程简化为匀速直线运动。

2 算例分析

以上文中建立的全过程外弹道数学模型为基础,采用MATLAB软件编制仿真程序,弹道仿真流程如图5所示。

图5 全弹道仿真流程图

2.1 全弹道仿真

选取投弹高度3 000 m、投弹速度150 m/s(水平投弹)、抛撒高度520 m、抛撒速度50 m/s作为仿真初始条件,给出航空末敏弹中第一层子弹的飞行弹道。为便于观察,将母弹飞行弹道和抛撒后的弹道分开表示,如图6、图7所示。图6中母弹高度降低到520 m时,母弹切割弹体,抛撒子弹。图7中,抛撒后的子弹经历减速伞开伞充气过程、减速过程、旋转伞开伞充气过程以及稳态过程,最终降落到地面上。当减速伞-末敏子弹系统的速度降低为80 m/s时,抛掉减速伞,拉出旋转伞。旋转伞-末敏子弹系统开始旋转并逐步实现对地面的稳态扫描,当高度下降为100 m时,子弹的水平位置基本不再发生变化,仿真截止。

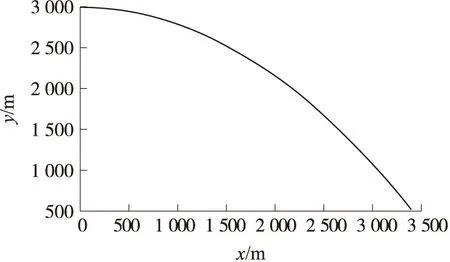
图6 母弹飞行阶段惯性系下垂直面内弹道轨迹

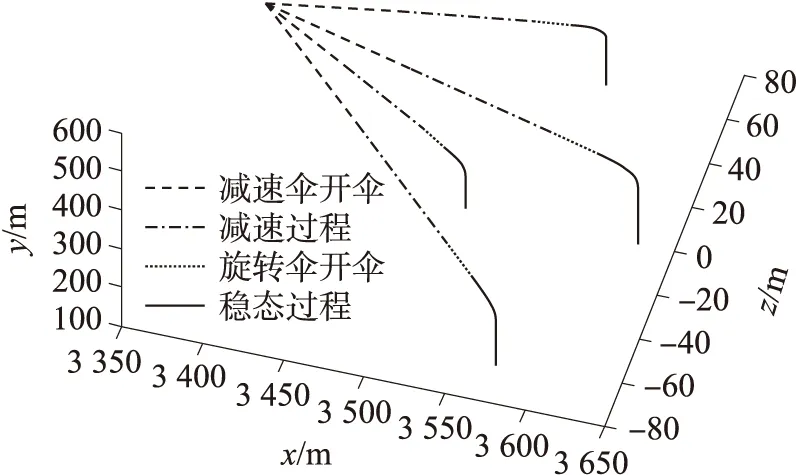
图7 4枚子弹脱离母弹后的弹道轨迹

图8是4枚末敏子弹形成的扫描覆盖区域,在此仿真初始条件下,z轴方向2枚子弹的扫描范围不重合,x轴方向的2枚子弹的扫描区域相互重合且与z方向子弹扫描范围重合。

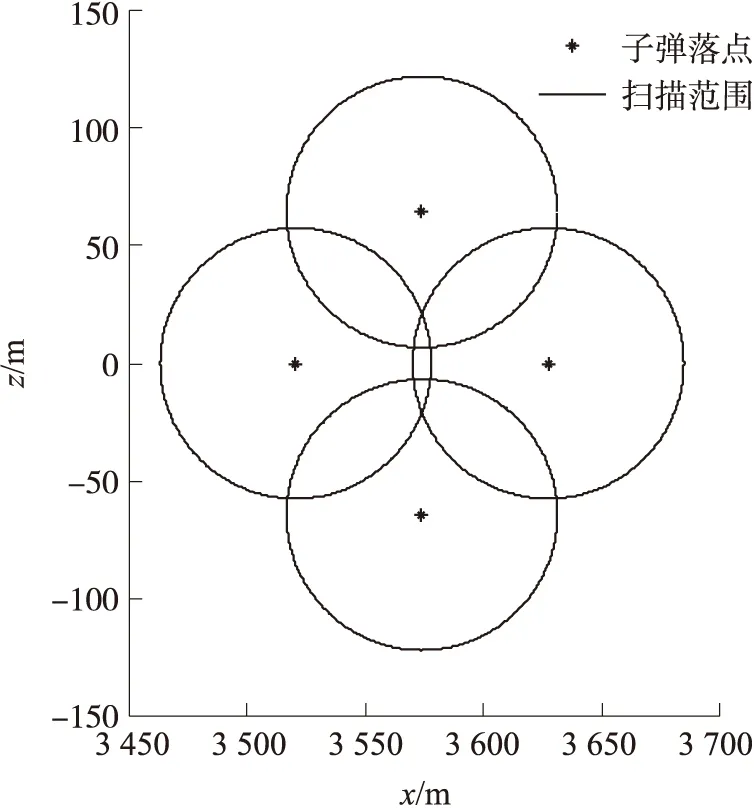
图8 一层末敏子弹的扫描区域

2.2 投弹速度对末敏子弹散布的影响

选取投弹高度为3 000 m、抛撒高度为520 m、抛撒速度为50 m/s作为初始条件,研究不同投弹速度对末敏子弹散布的影响。设定水平投弹速度分别为100 m/s,120 m/s,150 m/s,200 m/s,250 m/s,300 m/s,仿真得到的子弹落点散布如图9所示。采用一维cubic插值方法,得到落点x轴方向和z轴方向的间距随投弹速度的变化,如图10所示。

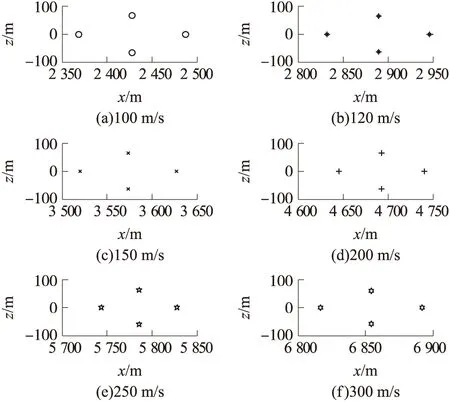
图9 投弹速度对地面散布的影响

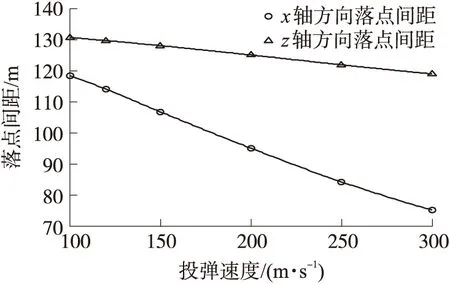
图10 落点间距随投弹速度的变化

由图10可见,x轴方向上的落点间隔与投弹速度成反比。这是因为投弹速度大,会使抛撒点的俯仰角的绝对值减小,这会降低抛撒点x轴方向2枚子弹的相对速度,进而降低x轴方向的落点间距。z轴方向上的落点间隔基本保持不变,受投弹速度的影响很小。这是因为一方面左右2枚子弹在抛撒点的侧向速度等于抛撒速度,与投弹无关;另一方面,垂直方向(y轴方向)上由投弹点到抛撒点为自由落体运动,所以投弹速度对伞弹系统的初始姿态有一定影响,但是对抛撒点的垂向速度没有影响,所以投弹速度对子弹降落到地面的运动时间影响不大。

因此,投弹速度对z轴方向的落点间距影响不大,在抛撒速度确定的情况下,x轴方向的落点间距与投弹速度成反比。在航空末敏子母弹的使用过程中,降低投弹速度可以使地面散布更为稀疏。

2.3 抛撒速度对末敏子弹散布的影响

选取投弹高度为3 000 m、投弹速度为150 m/s、抛撒高度为520 m作为仿真初始条件,抛撒速度分别设定为30 m/s,40 m/s,50 m/s,60 m/s,70 m/s和80 m/s,4枚子弹抛撒后的弹道轨迹如图11所示,子弹落点如图12所示,通过一维cubic插值给出了末敏子弹落点x轴方向、z轴方向的间距随抛撒速度的变化关系,如图13所示。

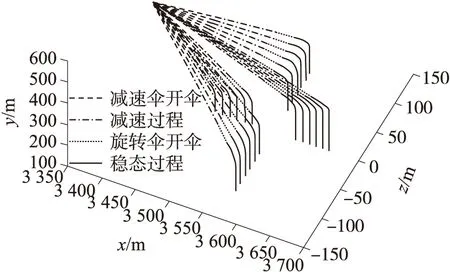
图11 不同抛撒速度下的弹道

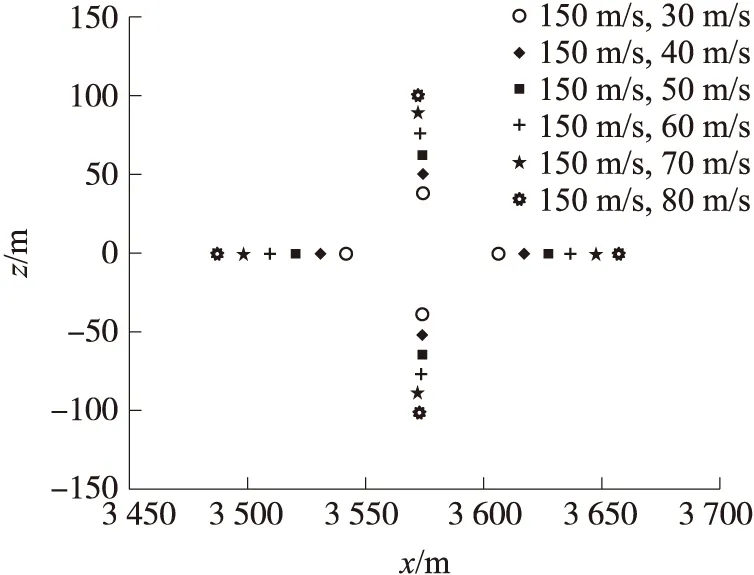
图12 抛撒速度对地面散布的影响

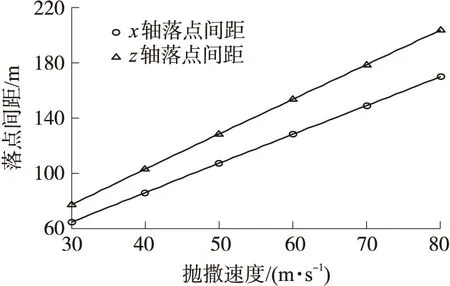
图13 落点间距随抛撒速度的变化

由图13可知,随着抛撒速度的增加,x轴方向上的落点间距与z轴方向上的落点间距均线性增大,表明落点间距与抛撒速度成正比。结合2.2节中的分析可知,水平投弹速度和抛撒速度均对x轴的落点间距有影响,而z轴方向的落点间距主要由抛撒速度决定。在航空末敏弹的设计使用过程中,应根据装甲目标队形合理确定投弹速度和抛撒速度。

3 结束语

本文设计了一种简易的航空末敏弹构型,建立了母弹飞行过程、减速过程、稳态扫描过程的全弹道数学模型,研究了一层末敏子弹的地面散布问题,基于MATLAB软件仿真分析了不同的载机水平的投弹速度和抛撒速度对末敏子弹地面散布的影响。研究结果表明:子弹散布x轴、z轴方向的落点间距与抛撒速度成正比;载机的水平投弹速度对末敏子弹散布x轴方向的落点间距影响较大,对z轴方向的落点间距基本没有影响。本文的研究内容能够为航空末敏弹的设计和使用提供依据和借鉴。抛撒高度、气象风、运动参数随机误差等因素也会对子弹地面散布产生影响,后续会结合蒙特卡洛方法研究这些问题。