自适应非奇异快速终端二阶滑模制导律
2020-07-06张宽桥
杨 芳,张宽桥,余 磊
(1.西安航空学院 飞行器学院,陕西 西安 710077;2.洛阳电子信息装备试验中心,河南 洛阳 471003)
在现代战争中,许多导弹(如某些反舰导弹、反坦克导弹、防空导弹等)需要以一定的攻击角度命中目标,来增加战斗部的毁伤效能。因此,攻击角度约束是制导律设计需要考虑的问题[1]。由于滑模变结构控制在滑动模态对干扰具有不变性,被广泛应用在制导律的设计中。文献[2]采用弹目视线角速率和视线角约束项作为滑模面,将滑模变结构控制用于带攻击角度约束的制导律设计中。文献[3]结合自适应指数趋近律设计制导律,增加了制导律的自适应性和动态性能。
上述制导律均采用线性滑模面,不能保证系统状态的有限时间收敛,而导弹攻击目标的时间是有限的。针对有限时间收敛问题,文献[4]基于终端滑模控制,设计了带攻击角度约束的有限时间收敛制导律。文献[5]通过在终端滑模面中加入线性项,进一步加快了系统状态的收敛速度。但终端滑模控制律中含状态量的负指数项存在奇异问题。针对奇异问题,目前主要有2种解决途径:一是非奇异终端滑模[6],二是积分滑模[7]。积分滑模能保证系统状态的有限时间收敛,但不能确定其具体的收敛时间表达式。文献[8]改进了非奇异终端滑模面,避免了奇异问题,并设计了相应的制导律,但所提制导律不能保证滑模面的严格有限时间收敛,存在非收敛因子,会降低收敛速率。文献[9]对滑模面的非严格收敛问题进行了研究,提出了一种严格有限时间收敛的非奇异终端滑模面,但滑模面函数是不光滑的,系统只能收敛至一个有界区域内,且无法给出其具体范围。
针对目标机动和系统扰动等干扰问题,目前大多数文献的处理方法有3种:设计干扰观测器实时在线估计干扰[10];设计自适应律估计干扰的上界[11],利用滑模控制的鲁棒性抵抗干扰。这些方法需要引入符号函数项,使得控制量不连续,引起抖振现象。大多数文献对符号项进行光滑处理,以达到削弱抖振的目的,但同时也削弱了滑模控制的鲁棒性。针对抖振问题,文献[12]提出了一种二阶滑模超螺旋算法,具有算法简单、避免抖振、鲁棒性强等优点。文献[13]采用该方法设计了二阶滑模制导律,能够有效抑制抖振,且能实现系统状态有限时间收敛。但超螺旋算法存在控制律不光滑,参数选取需要已知系统干扰的上界信息以及系统状态距平衡点较远时收敛速度慢等问题。
针对上述问题,本文设计了一种非奇异快速终端滑模面,改进了一种自适应光滑超螺旋算法来削弱抖振和抵消干扰,进而提出了一种带攻击角度约束的非奇异快速终端二阶滑模制导律,并对其有限时间收敛特性进行了证明。最后通过仿真验证了该制导律的有效性和优越性。
1 问题描述及相关引理
1.1 问题描述
在惯性坐标系上建立弹目相对运动关系如图1所示。r为弹目相对距离,q为弹目视线角,vm和vt分别为导弹和目标的速度,θm和θt分别为导弹和目标的航迹角。所有角度逆时针方向为正。

图1 弹目相对运动关系
根据弹目相对运动关系,可得弹目相对运动方程:
(1)
(2)
攻击角度为制导终端导弹与目标速度矢量方向之间的夹角。若导弹在命中目标时满足期望攻击角度,则有以下条件成立:
(3)
θd=θt(tf)-θm(tf)
(4)
式中:tf为导弹命中目标的时刻,θd为期望攻击角度。
将式(1)中第2个公式代入式(3),得:
vmsin(q(tf)-θm(tf))=vtsin(q(tf)-θt(tf))
(5)
将式(4)代入式(5)可得期望攻击角度与终端视线角q(tf)有如下对应关系:
(6)
因此,攻击角度约束问题就转化为了终端视线角约束q(tf)=qd的问题,其中,qd为期望终端视线角。
对式(2)整理后可得带攻击角度约束的制导系统状态方程为
(7)
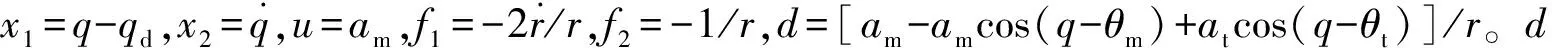
1.2 相关引理
为分析和证明方便,引入如下引理。
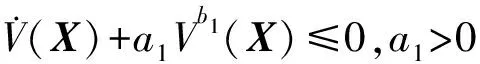
(8)
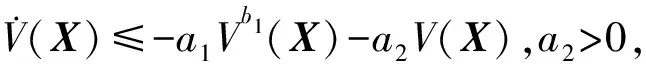
(9)
引理3[16]对于如下非线性系统:
(10)
若a1>0,a2>0,0
(11)
(12)
2 自适应二阶滑模制导律
2.1 制导律设计
终端滑模控制采用非线性函数作为滑模面,能够使系统状态有限时间收敛,但该方法存在奇异问题。为避免奇异问题,基于分段滑模面思想和引理3,设计一种非奇异快速终端滑模面为
s=x2+k1|x1|α1sgn(x1)+k2ψ(x1)
(13)
(14)
式中:α1>1,0<α2=p1/p2<1,k1>0,k2>0,δ>0,p1和p2为正奇数,λ1=(3-α2)δα2-1/2,λ2=(α2-1)δα2-3/2。
对式(13)微分得:
(15)
(16)
将式(7)代入式(15)得:
(17)
设计等效制导律为
(18)
将式(18)代入式(17)得:

(19)
为抵消干扰和抑制抖振,并加快滑模面的收敛速度,采用二阶超螺旋算法设计辅助制导律为
(20)
其有限时间稳定的充分条件为[17]
(21)
超螺旋算法能削弱抖振,且具有强鲁棒性和高精度的控制性能。但传统超螺旋算法有以下不足:①控制参数的选取需要已知干扰的边界信息;②当系统距平衡点较远时,收敛速度慢;③积分项下含有不连续项,控制指令是不光滑的,会影响控制性能。针对上述问题,对超螺旋算法进行改进,在控制指令中加入线性项,在积分项下加入连续函数,并设计了一种参数自适应律来抑制干扰。改进后的超螺旋算法设计的辅助制导律为
(22)
式中:1/2≤β<1。
参数自适应律为
(23)
式中:b>0,c>0,ε>0。
结合式(18)和式(22),设计制导律为
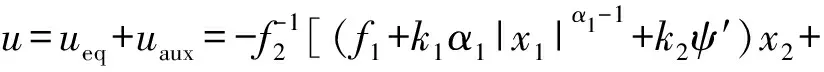
(24)
将式(24)代入式(17)得:
(25)
由式(25)可以看出,当系统状态远离平衡点时,式(22)中的线性项s起主要作用,相比传统超螺旋算法收敛速度更快,当系统接近平衡点时,非线性项|s|βsgn(s)起主要作用。因此,与传统超螺旋算法相比,式(22)具有更快的收敛速度。
由于系统会存在测量噪声,因此系统状态不能完全到达滑模面。为避免参数增至无穷大,因此自适应律中加入了sgn(|s|-ε)项,避免“过分估计”的问题[18]。
由式(22)可知,φ1(s)和φ2(s)与s同号,因此φ1(s)φ2(s)≥0。由式(23)可知,当|s|>ε时,k3和k4逐渐增大,使系统状态收敛。当系统状态收敛至|s|<ε时,sgn(|s|-ε)k3和k4逐渐减小。若k3和k4减小到无法抵消干扰时,系统状态会偏离|s|<ε,此时在自适应律作用下,k3和k4逐渐增大,使系统状态收敛至|s|<ε范围内。重复前面的过程,k3和k4逐渐减小。因此,k3和k4是全局有界的。
2.2 有限时间收敛性分析
对于系统总扰动d做出如下假设。
假设1d(t)表示为d(t)=d1(t)+d2(t),且满足:
(26)
式中:K>0,L>0。
一些文献假设系统干扰d有界且可微,但实际上,d可能包含有不可微的干扰信息,比如方波干扰、系统噪声等,因此假设1对d的描述较为全面,并且由于滑模面s并不会完全收敛至0,只是收敛至0的邻域内,式(26)是可以成立的。
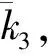
证明引入新的状态向量:
(27)
结合式(26)和式(27)可得,存在ρ1(t)和ρ2(t)满足:
(28)
对式(27)微分得:

(29)
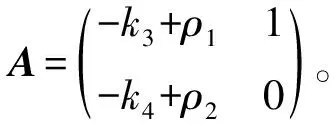
构造如下二次型Lyapunov函数:
V1=zTPz
(30)
(31)
式中:a为大于0的任意常数。易证P为正定矩阵且V1径向无界,即:
λmin(P)‖z‖2≤V1≤λmax(P)‖z‖2
(32)
定义一个正数σ满足0<σ<2b,结合式(29)对V1求一阶导数,得:
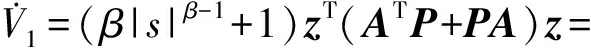
(33)
定义:
(34)
易证Q为半正定矩阵。
由式(32)可知:
(35)
(36)
由引理2可知,z可有限时间收敛至原点,即s是有限时间收敛的。
证毕。
定理2在制导律(24)的作用下,且制导参数满足式(23),制导系统状态可有限时间收敛至如下区域:
(37)

(38)
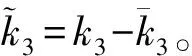
(39)

由式(36)可知:
(40)
当|s|>ε时,结合式(23)得:
(41)
令c>a,结合式(40)和式(41)得:
(42)
式中:
由1/2≤β<1,可知1/2<γ<1。由引理1可知V2可有限时间收敛至原点,因此,s可收敛至|s|≤ε,收敛时间满足:
(43)
当|s|≤ε时,若k3和k4减小到无法抵消干扰时,系统状态会偏离|s|≤ε,此时在自适应律作用下,k3和k4增大,使系统状态收敛至|s|≤ε区域内。
当滑模面s到达收敛域后,此时令s=ε1,则|ε1|≤ε。分以下2种情况进行讨论。
①|x1|≥δ,式(13)可写为
(44)

(45)
由于ε为一个较小正数,通过合理的选取参数k1和k2,可使2ϑ≤δ,此时,x1的收敛域为
|x1|≤max{2ϑ,δ}=δ
(46)
结合式(44),可得x2的收敛域为
|x2|≤k1|x1|α1+k2|x1|α2+|ε1|≤k1δα1+k2δα2+ε
(47)
②|x1|≤δ,式(13)可写为
(48)
由式(48)可得:
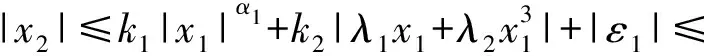
(49)
综上所述,系统状态可有限时间收敛至如式(37)所示的区域内,且收敛时间满足:
(50)
证毕。
制导律(24)中含有较多设计参数,这些参数可以根据实际需求来进行整定。对自适应律(23)和滑模面(13)进行分析可知,增大a,b,c,k1,k2和α1,减小β和α2的值,可加快系统收敛速度和控制精度,但也会增大导弹过载,而导弹的可用过载是有界的,因此在这些参数选取时要折中考虑。为后文叙述方便,将本节所提的自适应快速终端二阶滑模制导律简记为ANFTSG。
3 仿真分析
本节基于弹道仿真在不同场景下对制导律ANFTSG的性能进行仿真分析。在惯性坐标系下,设定导弹和目标的初始位置分别为(0,0)和(10 000 m,5 000 m),导弹的速度vm=500 m/s,目标运动速度vt=250 m/s。重力加速度g=9.8 m/s2,导弹的最大可用过载为20g。仿真步长0.01 s,采用4阶Runge-Kutta法解算仿真模型。ANFTSG的制导参数设置为:k1=k2=2,a1=7/5,α2=5/7,β=0.6,ε=0.01,δ=0.001,a=0.5,b=c=1。目标运动模型为
(51)
式中:xt和yt为目标在惯性系上的位置。
仿真中引入文献[8]提出的非奇异快速终端滑模制导律(NFTG)以及文献[13]提出的非奇异终端二阶滑模制导律(NTSG)进行对比仿真。
①仿真场景1。导弹以不同初始航迹角θm0打击机动目标。设定θm0分别为30°,60°,90°,120°,150°。期望终端视线角qd=45°。目标常值机动,加速度at=-30 m/s2,目标初始航迹角θt0=150°。仿真结果如图2所示。


图2 场景1的仿真结果
②仿真场景2。导弹以不同期望终端视线角打击机动目标。设定qd分别为20°,40°,60°和80°,θm0=45°,目标正弦机动,加速度at=30sin(πt/5),θt0=150°。仿真结果如图3所示。


图3 场景2仿真结果
③仿真场景3。ANFTSG和NFTG、NTSG对比仿真。设定θm0=45°,qd=45°,θt0=180°。目标的机动考虑如下2种情况:余弦机动at=30cos(πt/5),方波机动at=30sgn(sin(πt/5))。
引入平均过载nme来评估制导过程能量消耗,定义为
(52)
式中:N为总仿真步数。
仿真结果如图4、图5和表1所示。

表1为在3种制导律作用下的攻击时间、脱靶量、终端视线角误差和平均过载的仿真结果,可以看出,相比NFTG和NTSG,ANFTSG的攻击时间、脱靶量、终端视线角误差和平均过载最小。
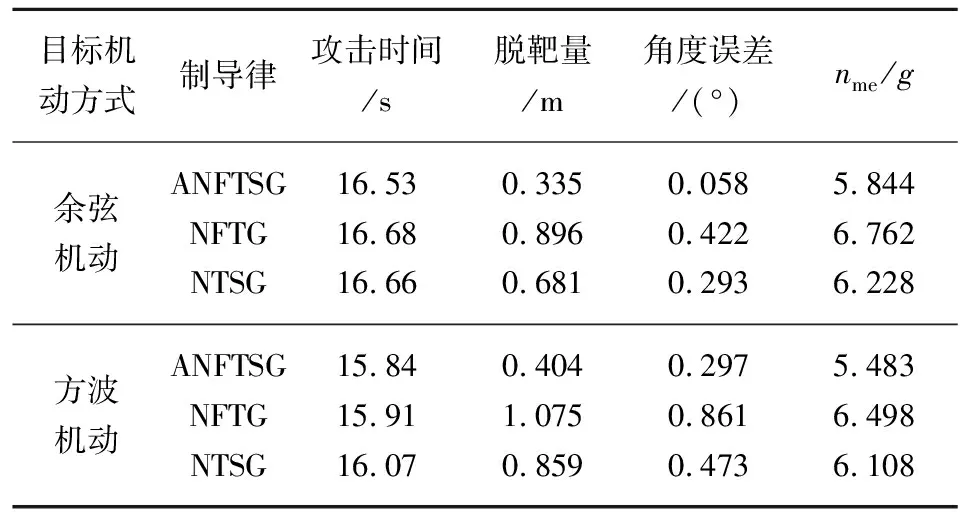
表1 不同制导律下的仿真结果
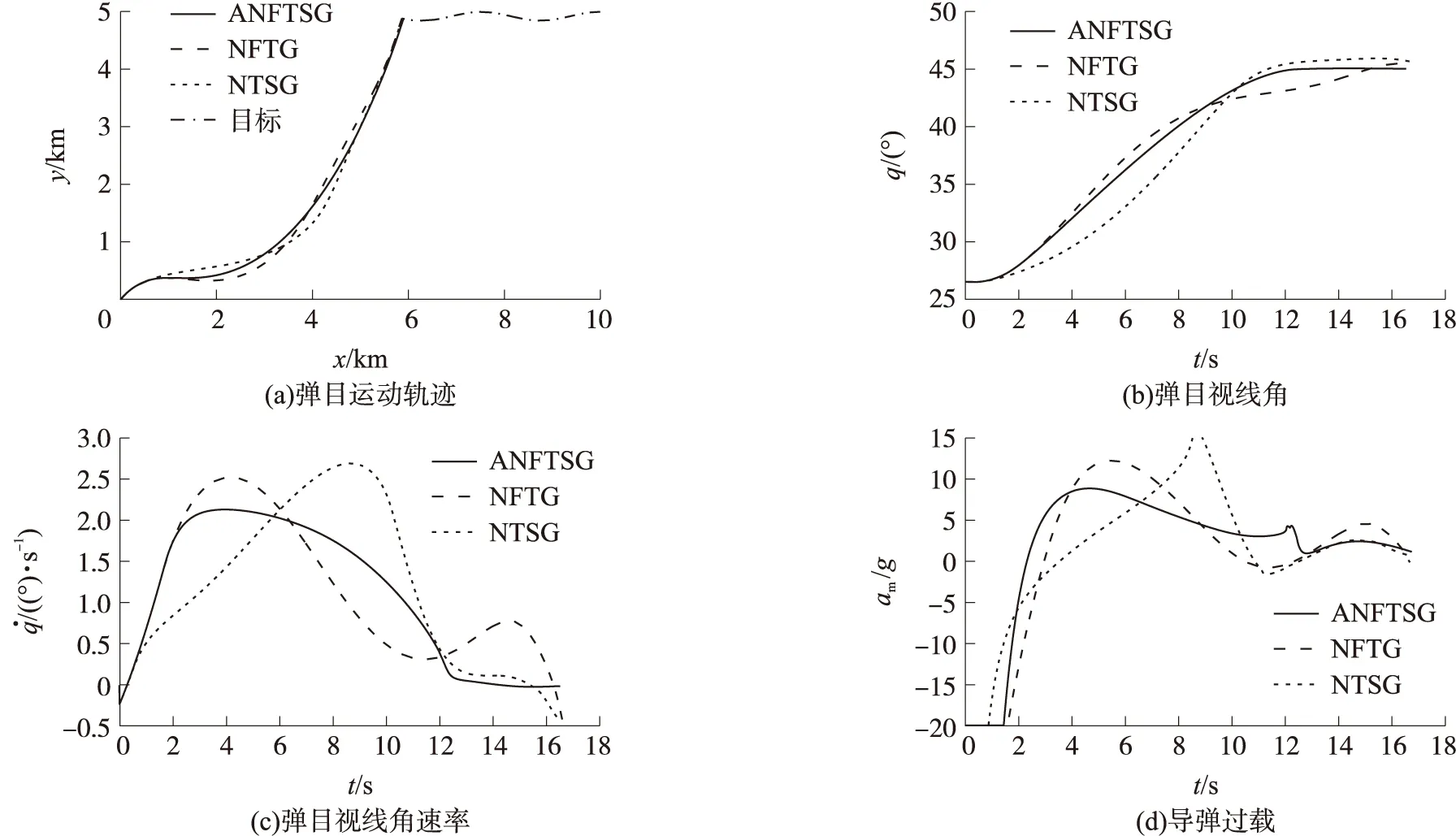
图4 目标余弦机动的仿真结果

图5 目标方波机动的仿真结果
4 结束语
本文针对机动目标,对带有攻击角度约束的制导问题展开研究。通过理论分析和仿真验证有如下结论:
①所提自适应非奇异终端二阶滑模制导律在存在目标机动不确定及系统扰动的情况下,能使导弹以期望攻击角度命中目标,并且使弹目视线角速率及视线角偏差有限时间内快速收敛至0的可控邻域内。相比现有的非奇异快速终端滑模制导律和非奇异终端二阶滑模制导律,制导精度更高,收敛速度更快,能量消耗更少。
②在超螺旋算法的基础上,增加了线性项和积分项下的连续函数,且设计了参数自适应律。一方面加快了系统的收敛速度,保证控制量的光滑性;另一方面能够自适应调整控制器参数,有效抑制系统干扰,且无需干扰的边界信息。
后续的研究可考虑将本文所提制导律扩展至三维空间,并考虑自动驾驶仪的动态特性。
