一道2019年摩尔多瓦奥林匹克试题的探究
2020-07-03上海市行知中学201999范广哲
中学数学研究(江西) 2020年6期
上海市行知中学 (201999) 范广哲
武汉职业技术学院商学院 (430074) 邹 峰
一、一道奥赛试题的证法
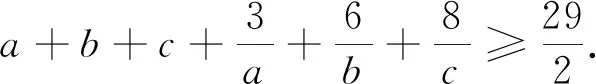
本文给出此题的证法,并对其进行拓展,给出一些变式与推广,希望对读者解题与命题有所帮助和启发.
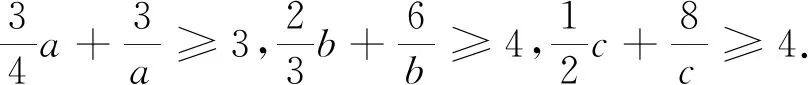
二、试题的探究
1.改变分式中的系数

令λ1=k,则λ2=3k-3,λ3=8k-16,其中k≥2,从而得到下列问题:






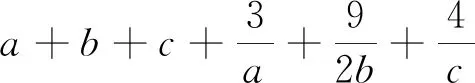
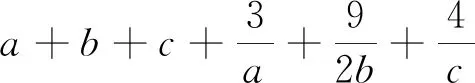


2.增加变量个数




三、试题的推广
按照上述解题方法,我们获得以下两个推广,留给有兴趣的读者探讨,本文不再赘述.



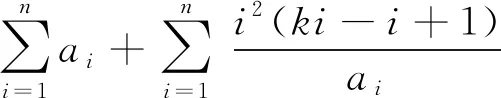
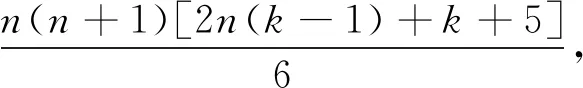
我们可以由这两个推广命题制出适合高考和竞赛的一些好的题目.例如,在推广1中结合问题2中当n=3,λ1=4,λ2=9,λ3=16可得:

在推广1中,当λi=(i+1)2(i=1,2,…,n)时,可得如下结论:

又如,在推广2中,当k=1,n=3可得:

在推广2中,当λi=i2(i=1,2,…,n)时,可得如下结论:

四、引申


