连续化简 多角度解决问题——一道试题的讲评历程

江西省萍乡中学 (337000) 贺 江

一、问题的提出

高一年级《解三角形》教学之后，有如下一道解三角形试题：

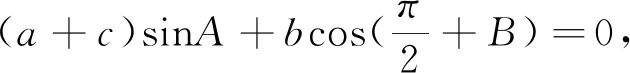
本题主要考查正弦定理、余弦定理的综合应用以及三角函数恒等变形能力.学生感觉本题难度较大，得分率极低.班级40位学生只有6位同学选对，其中只有3位同学能正确地说出解题思路及过程，远远低于教师的预期.笔者思考，学生解题过程可能存在一些误区，基于这个想法，笔者课前对学生的解题思维过程进行了调查，要求做对的几位学生写出他们的详细解题过程，未做对的几个学生也事先了解了他们的一些解题思路及困惑，了解思维受阻的原因.

解法1:原等式用诱导公式变形可得(a+c)sinA-bsinB=0(1).相当一部分同学由正弦定理“边化角”得sinA·sinC=sin2B-sin2A(2).

大部分同学做到此式就进行不下去了.

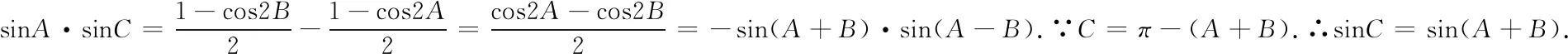
感悟:至此，问题已经解决，但是无疑此解法难度较大，对于大多数学生来说不能推广这个解法，这个当然也不是最理想的解法，必须要从另外的角度来分析.

二、另辟蹊径，一题多解

老师展示完上述解法，提醒学生对于(1)式，除了由正弦定理“边化角”之外，还有什么想法？

学生1：还可以根据正弦定理“角化边”为下式a2+ac-b2=0(4).

教师：(4)式可以联想到什么？

学生2：对(4)式的处理很容易联想到余弦定理，把“a2-b2”或“ac”与余弦定理中的“cosB”联系起来.

几分钟后.学生2给出以下解法：

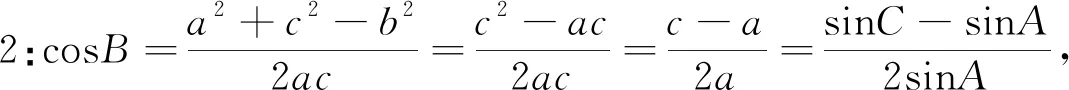
教师：解题的思考过程是一个连续化简的过程，即在充分研究和运用题目本身的特征提供的信息，联系已学知识，在完全合逻辑的前提下进行连续化简，一直到所得新题成为一项基础知识为止的过程.此解法正是联想到(4)式中式子的特征和余弦定理的关系进行连续合理的化简.

学生3：对(4)式的处理还可以联想到“a2-b2”与余弦定理“cosA”的关系.

学生4：直接利用余弦定理的另外一种形式，解法2和解法3都可以进行简化.

解法4:由余弦定理b2=a2+c2-2accosB,代入(4)式整理得ac=c2-2accosB,即a=c-2acosB(5).由正弦定理上式为sinA=sinC-2sinAcosB=sin(A+B)-2sinAcosB=sinBcosA-cosBsinA=sin(B-A).以下同解法1.

解法5：由余弦定理b2=a2+c2-2accosB,代入(4)式得ac=2bcosA-c2,即a=2bcosA-c(6).以下同解法3.

教师：(5)式和(6)式可以联想到锐角三角形中的什么定理？

学生5：由(5)式和(6)式可以联想到锐角三角形中的射影定理.

解法6：由锐角三角形中的射影定理得c=acosB+bcosA.结合由(5)式或(6)式，化简即a=bcosA-acosB.由正弦定理可化为sinA=sinBcosA-sinAcosB=sin(B-A).以下同解法1.

感悟:数学教师在实施课堂教学的过程中，要让学生能够把自己所学的所积累的解题经验总结并加工，并让它保存在自己的记忆当中，当遇到一个新的问题时，能够辨识它是属于哪一类基本问题，联想到这个已经解决的问题，以此为索引，在脑子里提取出解决这个问题的方法，为学生构建一条“从具体到抽象，从个别到一般，由此及彼”的思维通道，这一策略体现了“转化与化归”的重要的数学思想方法.