Bokov不等式的高维推广与加强

江苏省盱眙中学 (211700) 王 尧

1.引言

1966年E.A.Bokov给出了如下的不等式:

我们把上式称为Bokov不等式.

事实上，在顶点集为{A1,A2,A3,A4}的四面体Ω中，设hi为顶点Ai(1≤i≤4)所对面上的高，r为内切球半径,不难得出

等号成立当且仅当四面体Ω为正四面体.

本文主要是将上述不等式推广到n维欧氏空间Rn中去，并对不等式作系数上的新的推广，同时再给出它们的加强形式.

2.预备知识

定义[4]设Ω为n维欧氏空间Rn中的单形，其顶点集为A={A1,A2,…,An+1}，设P为n维欧氏空间Rn中的单形Ω所在空间中的任意一点，d1为点P到Ω的顶点Ai所对的界面的有向距离，又Ai所对界面上的高为hi(1≤i≤n+1)，则点P的重心坐标为

3.主要结果及其证明

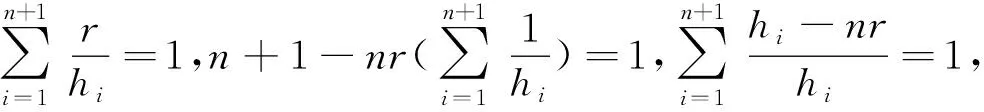
由Cauchy不等式[2]可得

推论1 在定理1的条件下，分别取n=2,n=3时,有

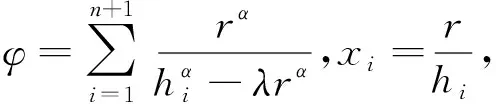
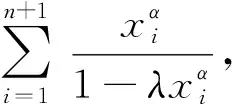
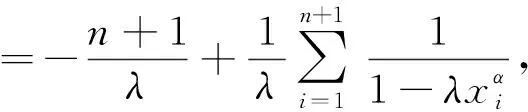
由拉格朗日恒等式[4]可得

推论2 在定理2的条件下，取λ=n,α=1,即为定理1结论.

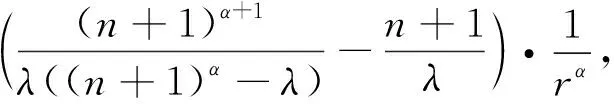
再由Jensen不等式[3]，则有