《数学通报》第2414号问题再推广

江苏省泰州市姜堰区南苑学校 (225500) 左小宁江苏省姜堰中等专业学校 (225500) 陈 宇

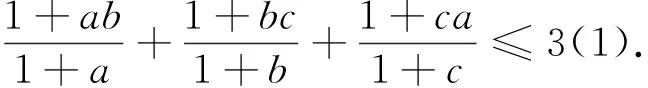
夏开平老师在文[1]中将该问题推广为：

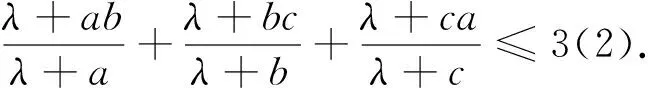
受其启发，笔者将该问题进一步推广为：

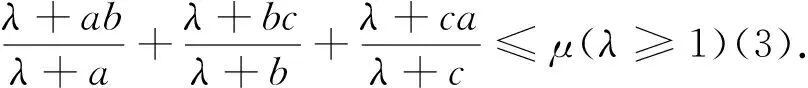
证明：∵a,b,c>0,a+b+c=μ，μ≥3，λ≥1，

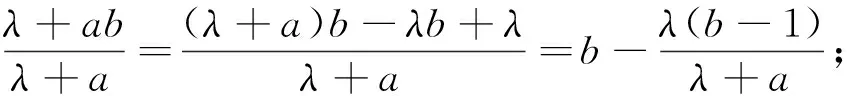
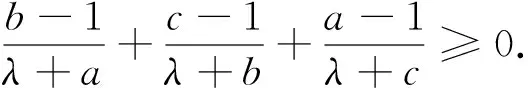
即证(b-1)(λ+b)(λ+c)+(c-1)(λ+c)(λ+a)+(a-1)(λ+a)(λ+b)=λ(a2+b2+c2)+(a2b+b2c+c2a)+(λ-1)(ab+bc+ca)+(μ-3)λ2-2λμ≥0(4).

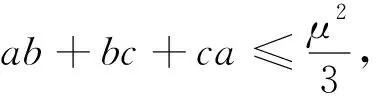
当μ=3时，即为文[1]之推广(2);

当μ=3，且λ=1时，即为《数学通报》第2414号问题(1).