例谈一个重要不等式在北大夏令营测试中的应用

新疆乌鲁木齐市教育研究中心 (830000) 赵爱华新疆生产建设兵团第二中学 (830002) 张国治

面对庞杂的知识体系和大量的模拟试题，如何针对竞赛展开高效的针对性复习？通过对近几年竞赛试题的研究，笔者有一个很有趣的发现——试题各异，出题角度多变，但探源溯流，它们来源于同一个问题．我们可以把这类不断衍生的题目称为“题根”．那么如何寻找“题根”呢？将源于课本的题目进行提炼与升华形成结论，然后再将其广泛应用于解题实践中，这便是寻觅“题根”的不二法门了.这一过程意义非凡，因为茫茫题海中很多题目表面不同，但实质一样(可归结于同一个“题根”)．一个“题根”加工而成的结论，其功效不亚于教材中的一个定理.[1]笔者从一个重要的不等式出发，探源溯流，给出其在北大夏令营测试中的应用.

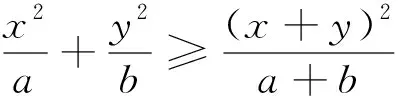
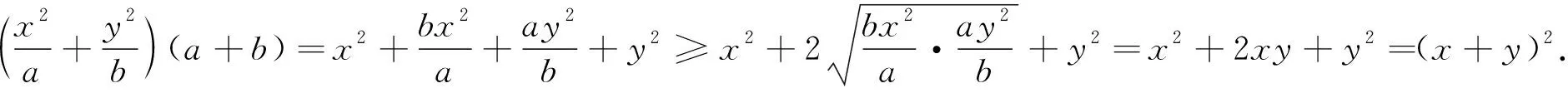
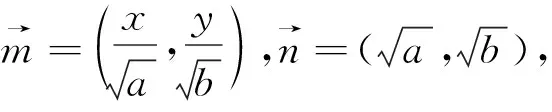
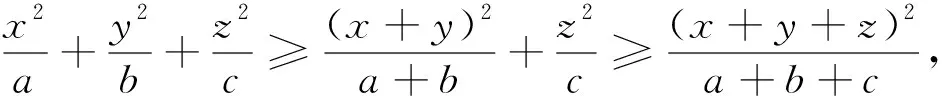
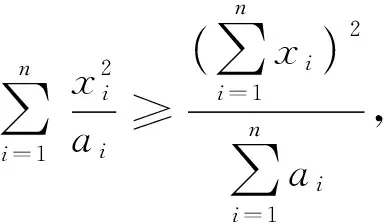
可以利用数学归纳法获得证明，过程略.

下面以北大夏令营测试题为例谈谈此不等式的应用，追本溯源，以期抛砖引玉，凸显回归题根的重要性.

分析：本题标准解答是平方后用二次函数求最值，但倘若利用本文的结论便有如下简洁明快的解答.

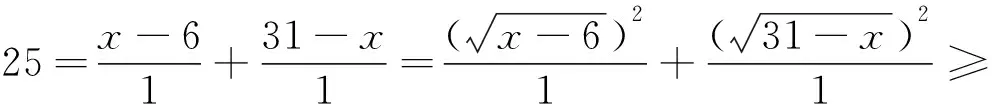
分析：本题标准解答是基本不等式求最值，但倘若利用本文的结论便有如下别开生面的解答.

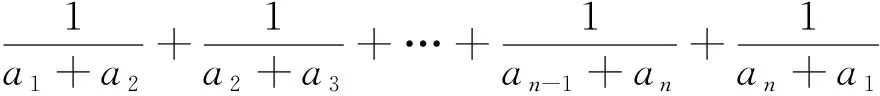
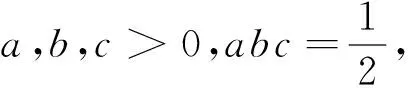
分析：本题标准解答利用重要不等式获解，但倘若利用本文的结论便有如下别具一格的解答.

例4 (2016年北京大学优秀中学生暑期学堂(综合营)试题第3题)设a,b,c为实数，证明：当且仅当(a-b)2≥2c时，对任意实数x都有(x-a)2+(x-b)2≥c成立.

分析：本题标准解答是构造二次不等式利用判别式获解，但倘若利用本文的结论便有如下别具一格的解答.

总之，研究“题根”对教学、命题和解题都有深远的意义，变幻多端的数学题目犹如葱郁繁密的树叶.看似难以捉摸，实则息息相关，故而在研究问题时应拨开层层枝叶，寻其根源，以本见全.