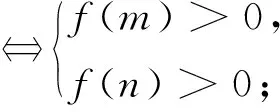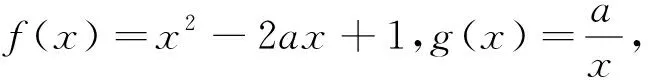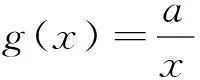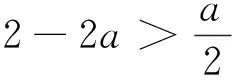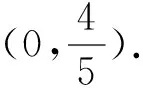例析处理恒成立与有解问题的若干策略

福建省莆田第二中学 (351131) 谢新华

在方程或不等式中，常遇到恒成立与有解问题，在恒成立或有解条件下求参数的取值范围问题．此类问题渗透着换元、化归与转化、分类与整合、数形结合、函数与方程等思想方法.其解题的基本思路是：根据已知条件将问题向基本类型转化，正确选用分离参数法、函数图像与性质法、数形结合法等解题方法求解．本文通过几个典型题目解析供参考.

例1 不等式x2+ax+2a+5>0在x∈R上恒成立，求实数a的取值范围.

解析:依题意由Δ=a2-4(2a+5)<0得-2

评析:本题化归为二次函数型问题，结合抛物线图像特征求解.一般地，设函数f(x)=ax2+bx+c，则f(x)>0在x∈R上恒成立⟺a=b=0,c>0或a>0且Δ<0；f(x)<0在x∈R上恒成立⟺a=b=0,c<0或a<0,Δ<0.

例2 不等式x2+ax+2a+5>0在x∈(-2,+∞)上恒成立，求实数a的取值范围.

解析2通过分离参数法，将问题转化为a>g(x)恒成立，再运用基本不等式求函数的最值，使问题获解.一般地，若不等式A>f(x)在区间D上恒成立，则等价于在区间D上有A>fmax(x)成立；若不等式B>f(x)在区间D上有解，则等价于在区间D上有B>fmin(x)成立.

例3 不等式x2+ax+2a+5>0在a∈(-6,-2)上恒成立，求实数x的取值范围.

(1)∀x∈[1,2]，都有f(x)>g(x)，求实数a的取值范围.

(2)∀x1∈[1,2],∃x2∈[1,2]，使得f(x1)>g(x2)，求实数a的取值范围.

当0

当1

评析:第(1)问等价转化为函数f(x)-g(x)>0恒成立，接着通过分离参数法，将问题转化为a<φ(x)恒成立，再运用导数法求函数的最值，使问题获解.第(2)问对不同变量对应的两个函数f(x)和g(x)分别求最值，即只需满足fmin(x)>gmin(x)即可获解．

(1)若∃x0∈(2,+∞),使f(x0)=m成立，求实数m的取值范围；

(2)若∀x1∈(2,+∞),∃x2∈(2,+∞),使得f(x1)=g(x2)，求实数a的取值范围.

评析:一般地，∃x∈D,使得f(x)=m，等价于m的取值范围是函数f(x)在D上的值域；对∀x1∈D1，∃x2∈D2,使得f(x1)=g(x2)，等价于函数f(x)在D1上的值域A是函数g(x)在D2上的值域B的子集，即A⊆B.

因为g(x)=ax-2a+2(a>0)在[3,4]为增函数，则g(3)≤g(x)≤g(4)，即a+2≤g(x)≤2a+2，即g(x)的值域为B=[a+2,2a+2].

评析:一般地，∃x1∈D1，∃x2∈D2,使得f(x1)=g(x2)，等价于函数f(x)在D1上的值域A与函数g(x)在在D2上的值域B的交集非空，即A∩B≠Ø.