一个分式不等式的进一步探究

重庆三峡学院数学与统计学院 (404000) 兰晨曦 黄 浩 陈晓春

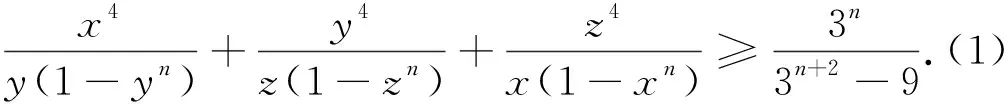
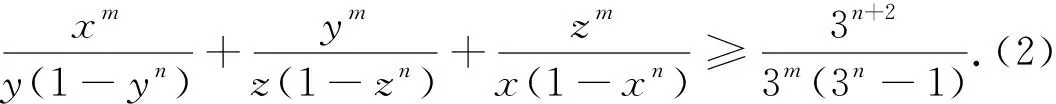
文[1]利用柯西不等式和幂平均不等式给出了(2)的证明，本文将利用广义权方和不等式的特例.，即下述不等式(*)和幂平均不等式对(2)给出更简捷的证明，并对(2)作进一步的探究.

为证明不等式(2)，引用不等式(其证明见文献[3]中定理3)：

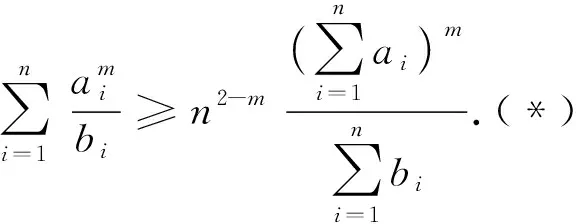
从而，不等式(2)成立.

上述证明的思路是：直接应用不等式(*)，因而不需任何技巧，同时从证明过程可以看出，只要(x+y+z)-(xn+1+yn+1+zn+1)不变，其证明过程是一样的，因此有：

探究1 将分母的顺序适当重排，其结论仍然成立，于是可得到如下与不等式(2)结构类似的不等式.

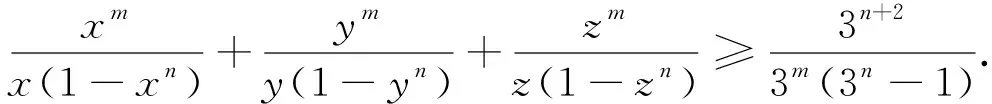
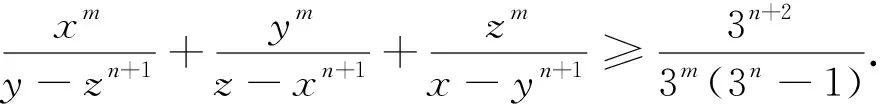
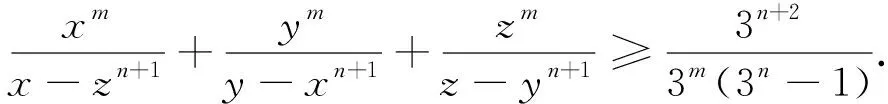
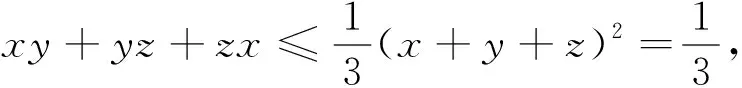
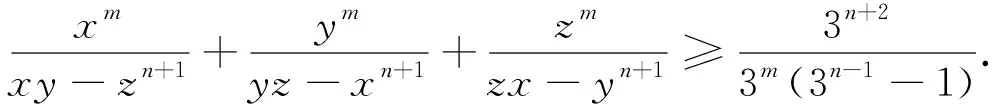
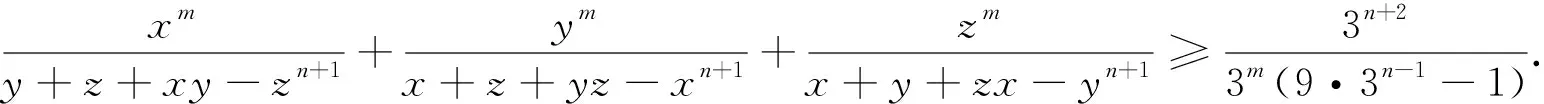
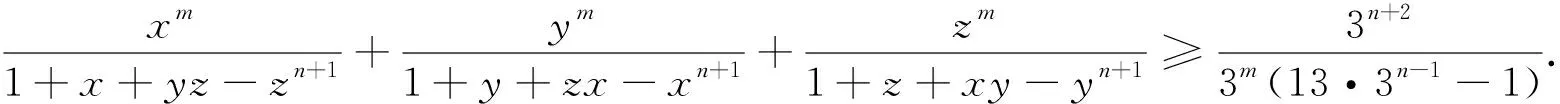
探究3 若将分母的每一项添加系数，则有如下推广的不等式.

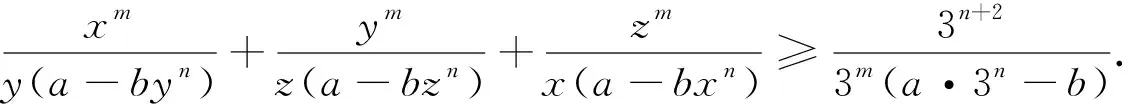
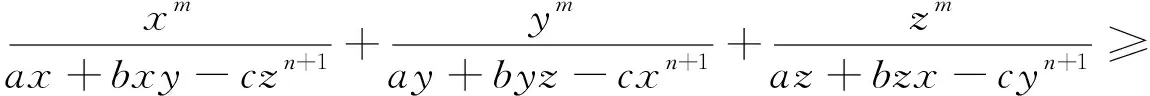
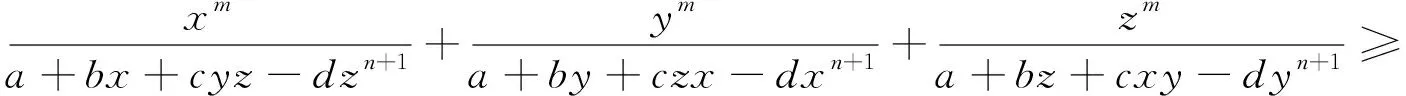
探究4 若将分子叠加，则有推广的不等式.

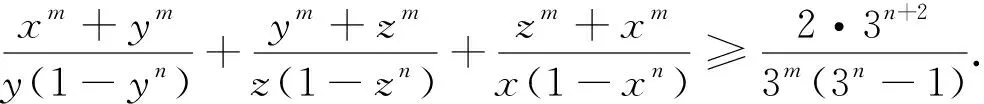
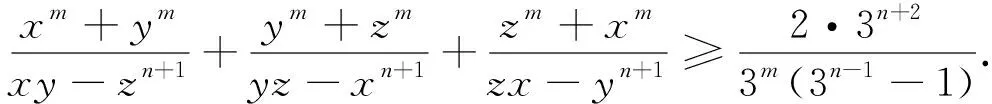
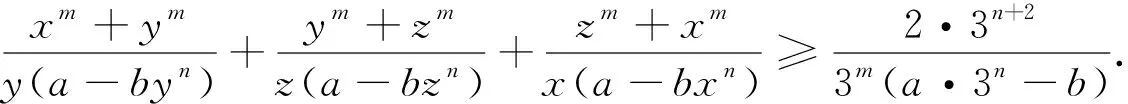
显然，对分母项的扩充及顺序重排不止上述几种，进一步扩充及重排将得到更多的不等式，有兴趣的读者不妨一试.另一方面从不等式(2)的证明可以看出，利用不等式(*)可将不等式(2)进一步推广.

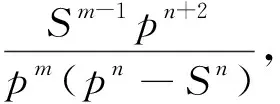
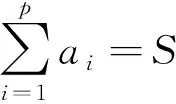
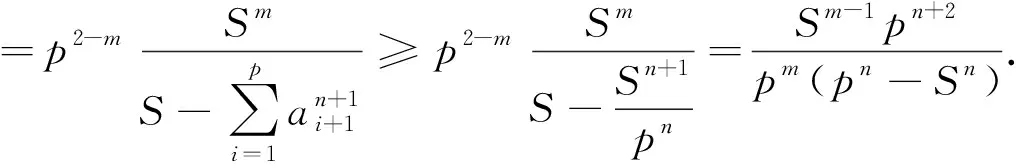
特别地，当p=3时，有不等式:已知x,y,z,n∈R+，m≥2，且x+y+z=S，求证：

同前面不等式(2)的探究一样，如果对不等式(3)，(4))的分母的项进行适当的重排及变式，可得到许多新的不等式，在此不再赘述.