小问题2020-3

《小问题》栏目欢迎来稿出题(请自拟题目或注明题目来源)，题目及解答请寄《力学与实践》编辑部，采用后将致薄酬。

2020-3如图1 所示，质量为M的方块以速度U与静止的质量为m的方块相撞。然后质量为m的方块与侧壁相撞，等等。整个过程完全弹性。求证：当M/m ≫1 时，总碰撞次数N与圆周率π之间有渐近关系式

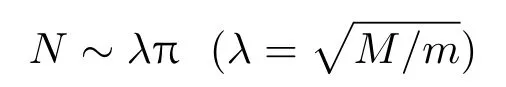
(当M/m=102k(k=1,2,···)时，计算表明，N就是π 之小数点向后移k位所得之整数。) (供稿：岳曾元)

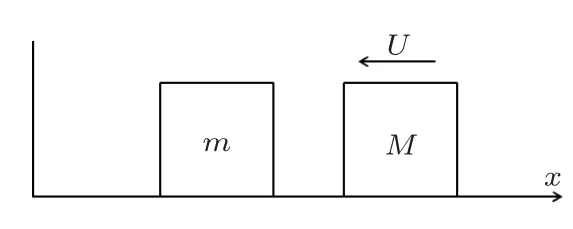
图1 初始状态

《小问题》栏目开展有奖竟答啦！2020年8月10日前将题目解答发送到lxsj@cstam.org.cn，解答正确者即可免费获赠《力学与实践》2020年第3期期刊1本 (来信时请注明邮寄地址)。期待您的参与！

* 《小问题》2020-2解答 *

问题：如图1所示，一陀螺由质量为m、半径为r的均质圆盘(厚度可不计)及通过盘心且与盘面垂直的直杆AB刚连后组成。直杆AB长为l，质量忽略不计，设l>r/2。陀螺铰接于铅垂轴Z上，当Z轴以匀角速度ω转动时，求：

(1) 陀螺的平衡位置(用AB杆与Z轴的交角θ表示)，并分析其稳定性。

(2)陀螺在稳定平衡位置附近微振动的圆频率。

(选自上海交通大学吴镇编《理论力学》下册22-22题，由江苏大学张孝祖改编并提供解答)

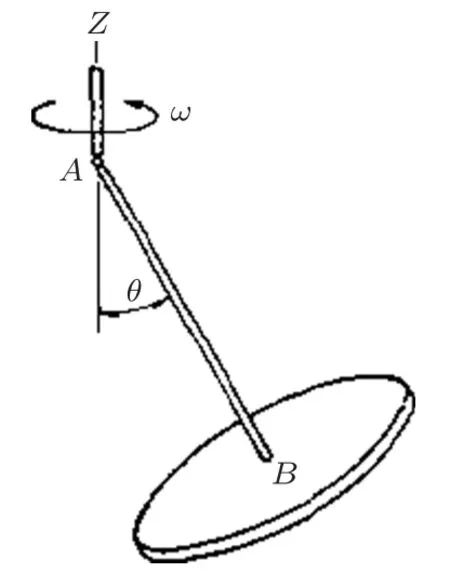
图1

解答：(1)陀螺绕A点作定点运动，建立陀螺的惯性主轴坐标系Axyz，如图2 所示，x轴垂直于杆AB与Z轴所决定的平面。陀螺对三个主轴的惯量为故有Jx=Jy >Jz。系统有1个自由度，取AB杆与Z轴夹角θ为广义坐标。

陀螺角速度矢Ω= ˙θi+ωsinθj+ωcosθk

陀螺动量矩H=Jx˙θi+Jyωsinθj+Jzωcosθk

陀螺动能

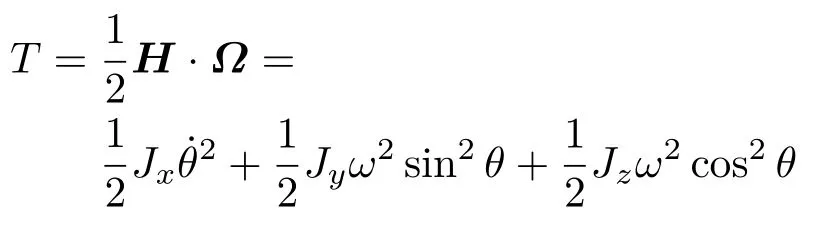
以A点为零势能位形，陀螺势能

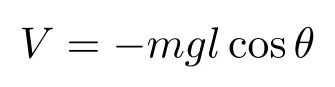
由于系统为非定常约束，陀螺动能T为的非齐次二次式

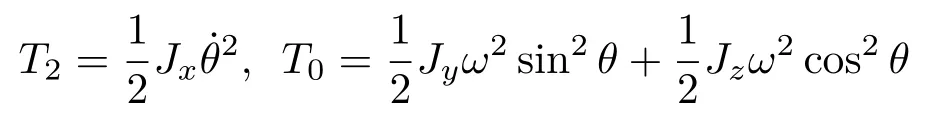
故系统广义能量守恒T2−T0+V=常量，即常量。

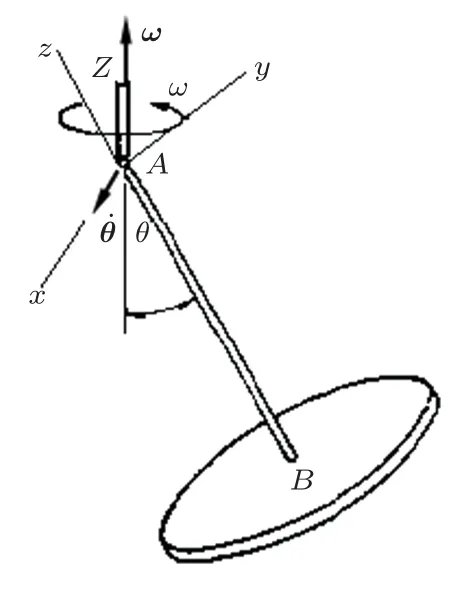
图2

其中，

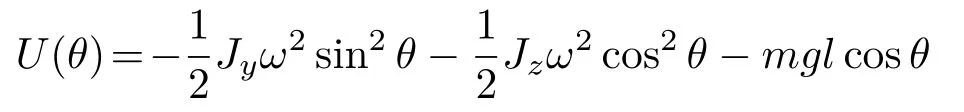
U(θ)为有效势能，利用U(θ)可确定陀螺的平衡位置及其稳定性。

由U′(θ)=0，可得

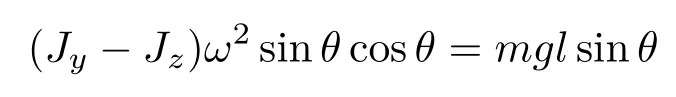
于是解得陀螺的平衡位置为θ1=0，θ2=π，

(另一平衡位置=−θ3不再讨论)

由U′′(θ2) =[(−Jy+Jz)ω2−mgl]可知，因Jy >Jz，有U′′(θ2)<0，故θ2=π的平衡位置是不稳定的，物理上不可实现。

(2)用U′′(θ)可求出陀螺在稳定平衡位置附近作微振动的圆频率。