跑步机上行走的彩虹圈
2020-07-02刘延柱
刘延柱
(上海交通大学工程力学系,上海200240)
1945年,一位叫詹姆斯的美国工程师偶然发现一个有趣现象,创造了一个取名slinky的新玩具[1]。刚一出现它就被抢购一空,几年内售出上亿只,成为20世纪美国发明的著名玩具之一。它的新奇之处是能自动下楼梯,动作十分诡异,曾获得“机灵鬼”的俏皮译名。后来涂上鲜艳的彩色,弯成弧形,如同天上的彩虹而有了“彩虹圈”这个更好听的名称。
彩虹圈是一个用金属丝或扁塑料带制成的软弹簧(图1)。它极其柔软,刚度仅为普通弹簧的百分之一。不受力时所有的螺圈相互接触,因此只能拉伸不能压缩。将弹簧折弯,双手托住弹簧的两端上下移动时,可以观察到螺圈向左或向右急速翻滚。将彩虹圈的两端置于楼梯顶部不同高度的两级台阶上,放手后其高端会突然跃起,弯曲,下降到低处台阶,然后另一端跃起,不断重复,直至楼梯的最底部完成下楼动作。
近来发现了彩虹圈又一个特殊本领。据网络报导,有人出于好奇将彩虹圈放在跑步机的传送带上,惊奇地看到它能不停向前翻筋斗,如同人的左右腿交替迈步似地走动起来(图2)[2]。报导中说明,做实验的跑步机后部必须垫高使传送带倾斜。彩虹圈在倾斜传送带上行走就和下楼有了相似之处,均为从高处往下降。差别在于,水平的台阶平面变成了斜面,固定支承变成了动支承。彩虹圈仿佛在一个无限延长的自行坡道上行走。笔者曾对彩虹圈的自动下楼现象做过解释[3-4],本文对跑步机上的行走现象再做些分析。

图1 平面上的彩虹圈
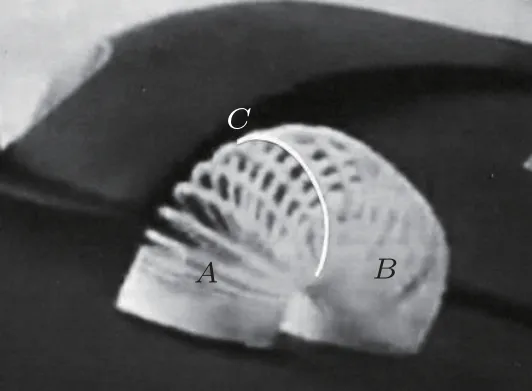
图2 倾斜传送带上的彩虹圈
将弯成弧形的彩虹圈放在倾斜角为β的传送带上,可看到接触面附近的弹簧压紧形成短圆柱,前方圆柱的高度大于后方,其余部分变形为圆拱状。以圆弧最高点C处的截面为界,将彩虹圈划分为前后两个隔离体。将较短的后半段记作A,前半段记作B(图2),质量分别为m1和m2,m1< m2。为便于分析,将圆拱部分视为连续的弹性体。由于弯曲变形,C截面有弯矩产生,将B作用于A的弯矩记作M1,A作用于B的弯矩为M2=−M1。弯矩的模均为kσ,以同一符号M表示。k和σ分别为彩虹圈的抗弯刚度和C截面处中心线的曲率。C截面处软弹簧的轴向拉力远小于重力和支承力,为简化分析予以忽略,其对质心的力矩设已被包含在弯矩项M1和M2之内。
以速度v向后匀速运动的传送带作为参考系。先考虑A段,设端部的法向约束力为Fn1,传送带运动引起的切向摩擦力为Ft1(图3)。Fn1在端面上的作用点为P1,端面中心为O1,质心Oc1在端面上的垂足为Q1,定义以下线段
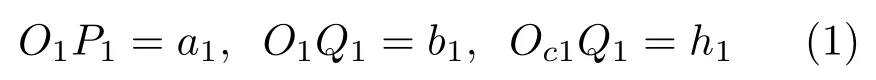
列写彩虹圈的平衡方程
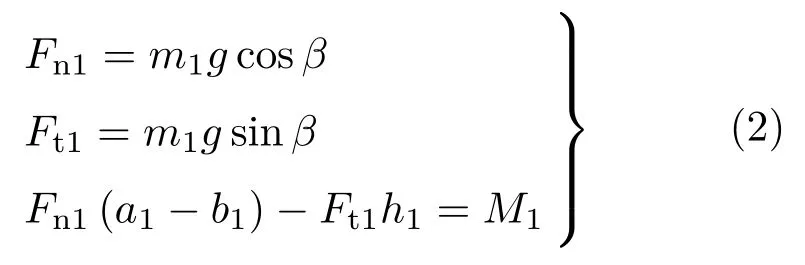
法向约束力Fn1仅当作用点P1在端部的接触范围以内时方可能产生,即a1必须小于端部圆环的半径R。从方程组(2)解出a1,得到A段与传送带保持接触的必要条件
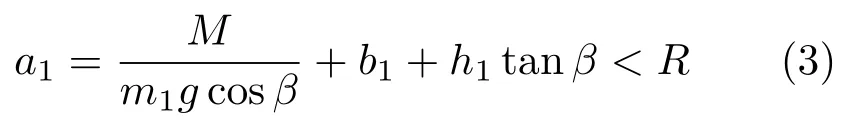
对B段作类似分析,将各字符的下标1 换成2。得到类似的约束存在条件,仅第3 项的正号变为负号,即
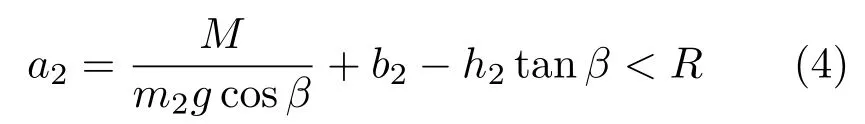
如传送带水平,即β=0,则A段与B段完全对称,如图1。m1和m2均为总质量之半,记作m0,且a1和a2,b1和b2相等,分别记作a0和b0,条件(3)和(4)均简化为同一条件

如彩虹圈在匀速运动的水平面上能保持平衡,表明此条件已自行满足。
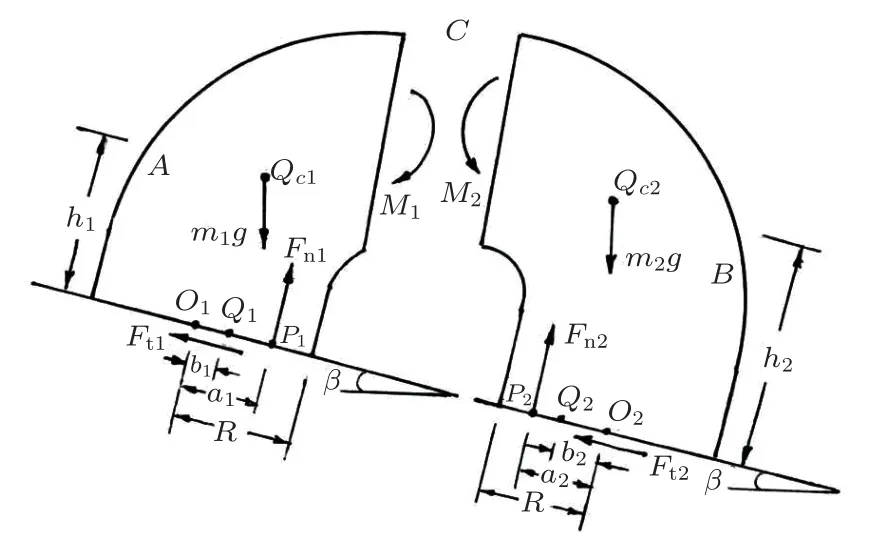
图3 彩虹圈A 段和B 段的受力图
若传送带倾斜,β0,则A段与B段不再对称。就B段而言,将式(4)与式(5)对比,因m2> m0,且增加的第3项为负值,则a2
在上述运动过程中,前方的B段起支承腿作用,后方的A段相当于摆动腿。当A段摆动到前方再次与传送带接触时,彩虹圈就完成一个走步。接着A段和B段互换角色,A段变为支承腿,B段变为摆动腿。前后段与传送带之间的约束从产生到消失再到产生,不断周期性循环,彩虹圈就能继续不断地向前跨步。约束状态在运动过程中发生变化的动力学系统称为变结构系统。能自动下楼和在跑步机上行走的彩虹圈就是典型的变结构系统。
除了会下楼和走步,彩虹圈还有别的一些奇特现象。例如手执彩虹圈一端使其向下悬垂。突然松手,彩虹圈不立即下落,而是在空中保持片刻静止。同时各圈从顶端开始依次向下压缩弹簧,直至压缩到最下端后方开始下落。要解释此现象,可先观察一下悬垂的弹簧在重力作用下的间距变化(图4)。最上一圈弹簧因承受彩虹圈的全部重量,有最大的拉力和间距。随后往下递减,至最下端弹簧拉力减小到仅与单个环的重力平衡。在松手的刹那,失去支承力的最上圈被弹簧拉动产生最大加速度,往下加速度依次递减。以致各圈从顶端开始依次往下压缩。当压缩引起的弹簧间距变化传到最下圈以前,最下圈的初加速度和初速度均为零,仍保持瞬间静止。压缩过程中因总质心下移产生的惯性力与重力平衡。待短暂的压缩过程结束时,彩虹环方开始整体的自由落体运动。

图4 悬垂的彩虹圈