为理解而教

张 鹤（北京市海淀区教师进修学校）

一、什么是对数学知识的理解

理解的过程常常伴随着各种各样的误解。也可以说，学生对教学内容可能知道但并没有理解。因此，真正的理解意味着洞悉支持数学知识的内在依据，同时也能够把看似抽象的数学概念转换为一种有意识的、自觉的思维方式和方法。

因此，为了理解的教学就是要在教学的过程中，让学生能够依据学习内容自身的逻辑建立起符合学生认知水平的思维逻辑，让学生能够用数学的思维去理解数学问题。

理解在教学活动中如此重要，但现实是许多教学活动致力于通过讲授知识达到教学目标而并不关注学生是不是理解。我们经常能够看到一些教师，以课时不足为借口，减少有利于促进学生理解所应该进行的分析问题、解决问题的思维活动，不讲知识的形成过程，不引导学生分析问题的背景，不关注数学问题产生的本质。

教师都是把“通过教学使得学生理解并掌握所教授的内容”作为自己的教学目标的，但最终的教学效果却是千差万别，其根源在于对理解的含义各有各的认识。在数学教学中，我们常常看到一些学生的数学学习总是停留在记结论、记公式，套用一些解题的方法，学生对数学概念的理解很浅薄，不深入，看不到数学知识本质的东西，掌握不了数学思考问题的思维方法。这些现象的出现很大程度上源于学生对数学知识的理解是单一的、平面化的。一些教师认为，只要在课堂上把所讲授的内容解释清楚了，那么学生就一定能够理解并掌握数学知识了。这样的教师满足于如何把课本知识以结论的形式尽快地让学生接受，并陶醉于学生能够很快正确地应用以及不错的检测成绩。而学生是否理解了这段知识背后的思维是什么，是否感受到了思考问题的过程，是否真正理解了所教授内容的本质则被忽略不计了。正是这样照本宣科式的教学没能够促进学生深入地思考数学问题、不会思考数学问题，使得学生对数学知识的误解和学习方法的误解一步步加深。

为了实现学生对数学知识的理解，实现学生对数学本质的理解，我们在教学中应当具有什么样的思维习惯呢？我们在教学中必须克服哪些盲点呢？这些问题就是属于理解问题能力的教学逻辑要解决的。合理的教学逻辑体系是建立在教师对新课程教育目标深入理解和对教学内容进行充分发掘的基础之上，并融合学生的实际情况及教师本身的教学风格而形成的。

从最根本的意义上讲，以理解为目的的教学要求尽可能地少讲以结论的形式呈现的知识。大部分理解与思考有关，对于思考来说，它是自己主动引发的结果，而不是通过训练产生的。在以理解性为目的的教学中，学生必须要意识到，理解的实现依靠自己领会，而不是等着记录老师的标准答案。作为教师不仅要改变教学内容的呈现方式，更重要的是要改变自己对教学意义的认识，在学生的认知规律中寻找逻辑主线。新课程强调学生的主体作用，教师的所有工作都是围绕“学的逻辑”而展开。

二、如何提高学生理解问题的能力

在课堂教学中，老师们常常提出各种各样的问题，以此希望能够引导学生对本节课的内容进行思考，进而提出新的问题并最终能够解决问题。应该说，通过问题的提出并解决是展开课堂教学很好的方式，也利于学生理解并掌握所要学习的数学内容。

数学问题不仅仅使得学习的内容更集中，而且数学问题还促进学生数学思维的培养。学生要想理解他们所知道的知识就会提出问题，在疑问中实现知识的建构。作为教师，当我们确立了一种教学目标并准备实现时，最为关键的策略是围绕问题设计教学的实施过程。这些问题可以为教师和学生提供明确的侧重点与更明确的学习方向，可以克服在教学实施过程中的随意性，也使得教学过程更具有连贯性。没有这些精心设计的问题的话，学生就有可能流于进行了一系列彼此无关孤立的学习活动，其效果就是阻碍了在学习中对数学观念及思想的理解与掌握。没有这些问题支配下的教师的教学活动，教学就有可能会沦为一种表面化、无目的的活动。如大量的教学内容在没有得到质疑、思考的情况下匆匆讲过，学生往往被讲糊涂了，而且讲的东西在学生的大脑中并不能留下深刻的印象，反而缺失了对核心问题的思考与建立在问答基础上的核心数学观念，学生记忆的负担达到了极限，其结果是思维方式的僵化。

在听课的过程中，经常看到的是教师的自问自答，即提出问题之后几乎没有给学生思考的时间或空间，教师自己就把答案给说出来了或给学生一些暗示，问题的价值打了折扣；还有一种情况是，提出的问题过于浅薄，学生几乎不假思索就可以回答，表面看课堂非常活跃，但其中数学的思维含量很小，没有深刻的问题能够引起学生之间、师生之间思维的碰撞，教学过程没有能够给学生带来观念上的理解与揭示，本该具有意义的教学变为一种表面化的、低效的、妨碍着学生理解数学问题的教学。究其根源，关键还是在于教师对课堂教学的价值和意义的误解。作为教师要知道：课堂教学的意义不在于教给学生一些结论性的东西，而是这些结论得出的过程；数学是以提高学生思维能力为主要目的，忽视思维过程的课堂教学是没有价值的，也是无效的。

在例题的教学中，很多教师的讲题没有把题目变成问题，而是按部就班式地讲解分析，就与学生看一道例题解答过程无异。在一节课中老师讲了若干道例题，但如果这些题目之间的逻辑关系不清、主题不清、要说明什么问题不清的话，就会出现学生“听明白了但自己做题就不会”的现象。

数学课上常常以题目作为载体本无可厚非，但作为教师要能够根据本节课的重点及难点，将具体的数学题目转换成一个个的数学问题，在提出问题、研究问题、解决问题的过程中提高学生的思维水平和能力。生动的数学课堂在于师生之间的数学思维的交流，如果把数学题目不加变化照搬到课堂上，就很容易将教学的过程变成一个解题的过程。解题更适合于学生在课后自己独立思考并加以解决，而不适合在课堂上通过大家交流来完成。

满足于正确答案而进行的教学，必然压制学生天然具有的对未知世界的探索欲望，只能使学生的思考和做事都变得刻板。对学生来说，如果认为自己的主要任务就是接受和重复真理，这必然会导致他们思维的呆板与对教师和教材的迷信和盲从。这样的教学会造成学生的理解及主动参与的意识渐趋萎缩，学生也就不可能实现对学习内容的真正理解。这样的数学内容也就沦为一系列事实与结论的堆积，学习的过程也就沦为一种没有问题的机械的接受过程。更为可怕的是，学生也就不喜欢数学学习。要使我们的课堂教学更具有吸引力，使学习内容更易于理解，我们在教学中就要坚持提出有思考价值的问题，不要急于给出答案，要通过问题引起悬念并激发学生不断地反思与追问。就像引人入胜的小说、电影一样，它们都是通过激起人们的疑问却不急于给出答案来吸引读者或观众的。

任何一名学生都厌恶死记硬背一些不理解的所谓的知识。作为数学教师，就是要在每一节的数学课中去创设问题的情景，让学生在这个情景中去体验思考数学问题带来的那种专注，去感受挑战困难、战胜困难的愉悦，充分享受数学的思维逻辑所带来的快乐。

三、教学案例

前几年流行的“学生会的老师就不用教”的所谓理念，看似深刻实则虚无。什么是“学生会的”？语焉不详，似乎课本上的知识学生能看懂，课本上的习题会做，就算学生会了，就可以不教了。暂且不说学生是否有足够强的学术研究能力，就是大学毕业的具有专业能力的教师不好好研究教材，都很难把知识所蕴含的思维、方法、学科观点教出来，我们又怎么能苛求中学生把课本上的知识学明白呢？

这样的理念也在误导着不少的青年教师。我曾经问过倡导这种理念的学校的一位青年教师：“你如何判断学生哪些是会的呢？”这位青年教师说：“很容易，讲题，学生都不会。”看似轻松的回答，让我听了很不是滋味。我要指导她录制一节课，在讨论教学设计的时候，她坦承都不会“教学引入”了，因为她上课不需要引入，不需要讲知识的形成过程，只需要讲学生“不会”的，也就是讲题了。可以看出，这样的“教育理念”不仅是耽误了学生，更耽误了一代青年教师的成长。

我们的教学对象是思维能力由弱到强、由感性到理性逐步发展的中学生，作为学科教师，就要能够通过我们所教授的知识为学生的成长提供有价值的教学。

如在7年级《相交线》这一章中的“三线八角”，教材是这样表述的：

如果按照“学生会的老师就不要教”的说法，这段知识肯定属于不用“教”的范畴了。当然，教师按照教材“照本宣科”地教也真是“白教”，因为没有教出东西来。

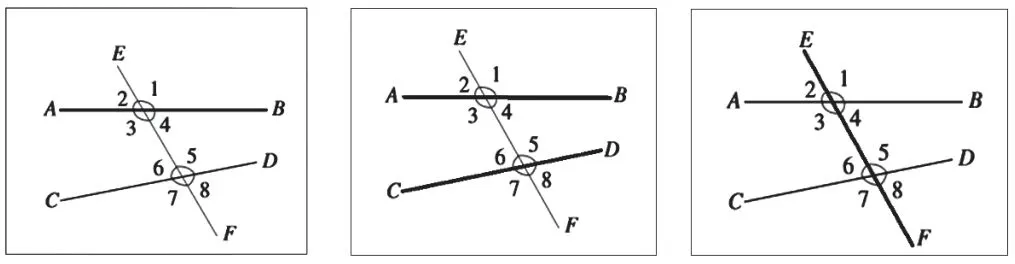
那么，应该如何“教”才算教到位呢？

我们首先需要明白：什么叫直线AB、CD 的“同一方”？什么叫直线EF 的“同侧”？学生如果只是由图形直接观察来理解的话，那还用学平面几何吗？实际上，这里面的“同一方”也好、“同侧”也好，表达的是几何“位置”的观点，而如何让“位置”变成学生的思维是需要教师进行教学设计的，直白地如教科书式的“教”，就不是指向学生思维的了。

可以这样来设计这段教学：

先画一条直线AB，如果进来一个不落在直线AB上的点P，它在哪里呢？这个时候就自然而然出现“位置”的思维了：点P 要么在直线AB 的上方区域，要么在直线AB 的下方区域；

如果再画一条直线CD，不经过这两条直线的点P又落在哪里了呢？点P 要么在直线AB、CD 的同一侧的上方区域；要么在直线AB 的下方区域且在直线CD的上方区域，即在两条直线AB、CD 之间的区域；或在直线AB、CD 同一侧的下方区域。

如果再画第三条直线EF 与直线AB、CD 都相交的话，那么，不落在这三条直线上的点P 的位置如何确定呢？显然，除了需要像前面那样通过直线AB、CD 确定位置之外，还需要由直线EF 来进一步地确定位置，即是在直线EF 的“同侧”还是“异侧”了。

这样的几何“位置”的观点不是学生自己看书就能够“看懂”的，更不是教师不需要教的，这样的教学设计体现出来的是教师的专业能力。