基于Riemann问题的可压缩多介质流体数值模拟及在二维爆炸冲击波传播问题中的应用
2020-07-01姚成宝付梅艳
姚成宝,付梅艳,2,闫 凯,2,韩 峰
(1.西北核技术研究院,陕西 西安 710024; 2.北京大学 数学科学学院,北京 100871)
引 言
可压缩多介质流动问题的数值模拟越来越受到人们的广泛关注,诸如爆炸冲击波、高速冲击等,都属于可压缩多介质流动问题的范畴。在多介质流动问题的数值模拟中,计算区域内可能会出现多种介质相互作用。界面两侧的介质通常具有截然不同的状态方程,且介质的初始状态也会存在较大差异,给数值模拟特别是界面附近的数值计算带来很大的困难。很多对单介质问题比较有效的数值方法在处理多介质问题时往往无法得到理想的结果,并且在界面处会出现非物理振荡,降低计算精度,甚至使计算难以进行。如何准确描述界面的位置以及界面两侧介质之间的相互作用,是求解多介质流动问题的关键。
在Euler坐标系下,目前应用较多、用于描述和追踪物质界面的方法包括两类:弥散界面方法和清晰界面方法。其中,弥散界面方法[1-2]将包含界面在内的几层网格上的物理量进行平滑磨光,形成具有一定宽度的平衡层。清晰界面方法将界面视为严格的接触间断,并清晰捕捉界面的位置,例如VOF方法[3]、Level Set方法[4]和Front Tracking方法[5]等。当确定物质界面的位置后,需进一步准确处理不同介质间的相互作用,常见的处理方法包括虚拟流体类方法[6-7]和切割单元法(Cut cell method)[8]。无论采用何种方法,如何确定界面上的状态参数是一个关键环节。由于物质界面实际上是一个接触间断,求解界面上的多介质Riemann问题精确解[9]是求解该类问题的最直接和有效的方法,其能够精确捕捉激波和接触间断的位置。
Riemann问题的求解和介质的状态方程密切相关,不同状态方程的Riemann问题求解也各不相同。对于形式比较简单的状态方程,Riemann问题可以表示为解析形式的代数方程并通过迭代得到任意精度的解,但工程应用中常见的状态方程通常具有比较复杂的形式,尚不存在Riemann问题精确解的通用计算方法,大多采用近似解来进行计算。例如,Banks[10]对JWL 状态方程的 Riemann 问题进行了分析,并利用二分法迭代求解接触间断上的压力p满足的代数方程。Kamm[11]在 Banks的基础上,针对满足凸性的一般状态方程建立了类似的数值求解方法。Rallu[12]、FarHat[13]和Lee[14]分别针对JWL 状态方程和Mie-Grüneisen形式的状态方程,建立了一个2×2的代数方程组,并通过迭代求解该方程组,获得了 Riemann 问题的近似解。
本研究在上述基础上,提出了一种针对JWL、多项式等高度非线性状态方程的多介质Riemann问题求解方法,能够对激波、稀疏波作用到不同物质界面时的复杂波系结构进行高效、准确的求解。结合前期工作[15-16],建立了一套能够模拟极端条件下、具有复杂状态方程的多种介质间相互作用的二维数值计算体系。最后,对Riemann问题的健壮性和精度进行了测试,并对水下、空气自由场以及密闭空间下的TNT爆炸冲击波传播过程进行了数值模拟,验证了数值方法的实际应用能力。
1 物理模型和数值方法
1.1 控制方程和状态方程
考虑二维计算区域上的多介质流体问题,基于Euler坐标系描述流体的动力学行为,控制方程组如式(1)所示:

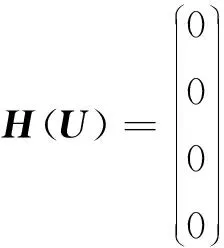
(1)
式中:ρ为密度;u、v为x、y方向的速度;E为单位体积总能量;p为压力,下同。
TNT爆轰产物采用JWL状态方程,如式(2)所示:
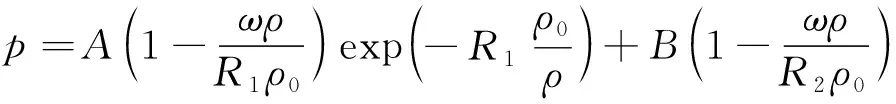
(2)
式中:ρ0为初始密度;e为单位质量比内能,且满足e=E/ρ-(u2+v2)/2;A、B、R1、R2和ω为JWL状态方程的参数,且A=3.712×1011Pa,B=3.23×109Pa,R1=4.15,R2=0.95,ω=0.3。
空气采用理想气体状态方程来描述,如式(3)所示:
p=(γ-1)ρe
(3)
式中:γ=1.4为空气的绝热指数。
水采用多项式状态方程来描述,如式(4)所示:
(4)
式中:μ=ρ/ρ0-1;A1、A2、A3、B0、B1、Γ1、Γ2为多项式状态方程的系数,且A1=2.2×109Pa,A2=9.54×109Pa,A3=1.457×1010Pa,B0=0.28,B1=0.28,Γ1=2.2×109Pa,Γ2=0Pa。
为后续进行统一分析,将JWL状态方程、理想气体状态方程和多项式状态方程写成统一形式:

(5)
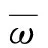
1.2 多介质流体数值方法
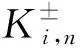
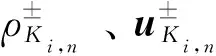
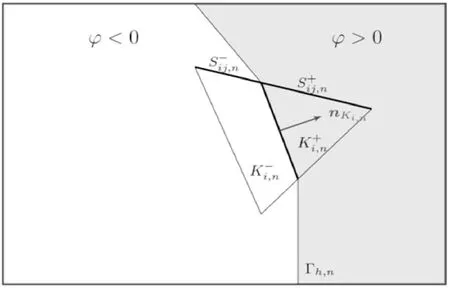
图1 多介质流体计算模型示意图Fig. 1 Schematic diagram of multi-media fluid calculation model
1.2.1 单元边界数值通量
单元边界的数值通量是指单元边界上同种流体之间的数值通量,且满足:
(6)
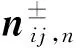
1.2.2 物质界面数值通量
物质界面数值通量是物质界面两侧不同流体之间的数值通量,且满足:
(7)

1.2.3 守恒量更新
当计算得到Ki,n的单元边界数值通量和物质界面数值通量后,可对该单元中每种流体的守恒量进行式(8)所示的更新:
(8)
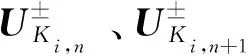
2 多介质Riemann问题数值求解
2.1 多介质Riemann问题
由于多维Riemann问题的复杂性,相关的理论研究十分困难,目前常见的做法是将多维Riemann问题简化为界面法向上的局部一维Riemann问题[9],利用界面两侧流体的压力和法向速度的连续条件来求解一维Riemann问题,此时Riemann问题可表示为求解式(9)所示的一维多介质Euler方程组的初值问题:
Uτ+F(U)ξ=0
(9)
式中:τ和ξ分别表示时间和空间坐标;
U=[ρ,ρu,E]Τ,F=[ρu,ρu2+p,(E+p)u]Τ,
且满足初值条件:

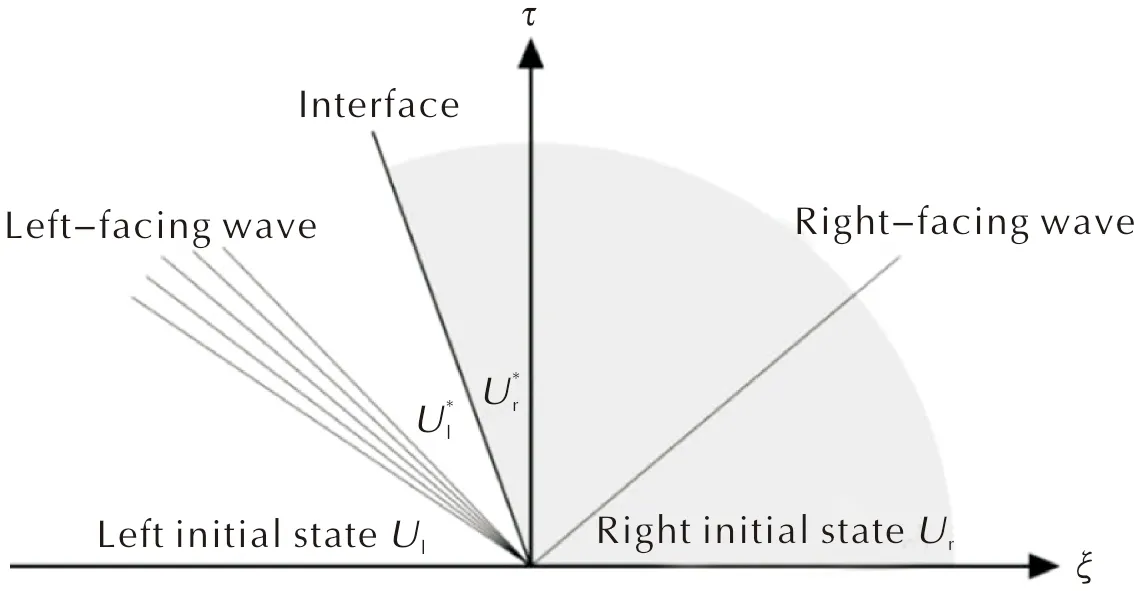
图2 一维多介质Riemann问题的波系结构Fig.2 Typical wave structure of one-dimensional Riemann problem

f(p)=fl(p,Ul)+fr(p,Ur)+ur-ul=0
(10)
其中,
(11)
式中:c表示声速,k=l,r。
利用牛顿迭代法对式(10)进行迭代求解,可得到界面上的最终压力p,此时界面上的速度u可表示为:
2.2 多介质Riemann问题的数值求解
对于JWL、多项式等形式复杂的状态方程,fl(p,Ul)和fr(p,Ur)具有高度非线性,解析求解式(10)非常困难。本研究采用数值方法来近似求解fl(p,Ul)和fr(p,Ur),并通过在数值求解过程中进行误差控制来保证近似解收敛到式(10)的精确解。
2.2.1 激波
当p>pk时,该非线性波的类型为激波。根据内能e的Rankine-Hugoniot关系:
(12)


(13)
利用牛顿迭代法对式(13)进行迭代求解:
(14)


2.2.2 稀疏波
当p≤pk时,该非线性波的类型为稀疏波,p和ρ满足等熵关系dρ/dp=1/c2。结合式(11)的稀疏波关系,可得:
(15)
利用自适应步长的Runger-Kutta-Fehlberg方法[17]对式(15)进行联立求解,可完成稀疏波分支fk(p,Uk)的求解。其中c表示声速,且满足:
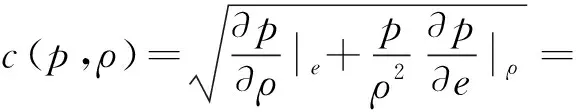
2.2.3 Riemann问题的求解步骤
综上所述,本研究提出的Riemann问题的整体求解步骤如下:
(1)提供物质界面压力的初始估计p0和整体误差阈值ε0,其中
(2)假设第n步迭代的值pn已知,确定左、右非线性波的类型:
①如果pn>max{pl,pr},两侧非线性波均为激波;
②如果min{pl,pr} ③如果pn≤min{pl,pr},两侧非线性波均为稀疏波。 (3)根据非线性波的类型和当前迭代步的局部求值误差εn,严格控制激波分支的非线性代数方程(13)的迭代残差和稀疏波分支的常微分方程组(15)的局部求值误差,计算得到当前步的fl(pn,Ul)和fr(pn,Ur); (4)更新得到n+1迭代步时,物质界面上的压力: (5)当压力的相对变化达到指定的整体误差ε0时,迭代终止,将得到的收敛解pn近似作为物质界面的压力p*,否则返回步骤(2)。 (6)计算物质界面上的法向速度: 利用本研究数值方法分别对强稀疏波Riemann问题和气-水多介质Riemann问题进行数值模拟,验证数值方法的精度和健壮性。另外,若无特殊说明,本研究所有算例均采用kg-m-s单位制,其中密度ρ、速度u和压力p的单位分别为kg/m3、m/s和Pa。 利用一个强稀疏波问题[9]对本研究设计的Riemann问题求解方法的健壮性进行测试。计算区域为[0,1]m,初始界面位于x=0.5m,界面两侧的介质均为理想气体,且初值条件如下: 将初值条件进行无量纲缩放,测试数值方法在不同的数量级下能否始终保持与解析解一致。其中,无粘、可压缩流体的无量纲关系满足p∝u3和p∝ρ3,即当u和ρ进行相同的量级变化后,p相应的变化3个量级。表1给出了在不同量级的初值条件下,数值模拟结果与理论结果的对比,可知本研究的 Riemann 问题求解器在不同量级的初值条件下均具有较好的一致性,验证了方法的健壮性。 表1 Riemann求解器的健壮性测试 计算一个气-水多介质Riemann问题,验证本研究方法求解多介质Riemann问题的精度。其中,气体采用JWL状态方程来描述,水采用多项式状态方程来描述。计算区域为[0,1]m×[0, 5×10-3]m,网格尺寸为2.5×10-3m。初始条件如下: 计算时间为t=8.0×10-5s。数值计算结果与参考解的对比如图3所示,对比结果表明本研究的数值方法能够准确地捕捉Riemann问题解的波系结构,且在激波和物质界面附近没有产生非物理震荡,说明本研究方法能够有效处理JWL和多项式等具有高度非线性的状态方程。 图3 JWL-多项式Riemann问题Fig.3 JWL-Polynomial Riemann problem 进一步利用数值方法分别对TNT水下爆炸、TNT空中爆炸自由场、柱形容器内冲击波反射等问题进行数值模拟,并将计算结果与实测数据进行比对,验证数值方法在爆炸冲击波问题中的应用能力。 首先计算100kg TNT在水下自由场中爆炸产生的冲击波传播过程,分别采用JWL和多项式状态方程来描述TNT爆炸产物和水介质。整个计算区域为[0,15] ×[0,4]m。为提高计算效率,利用H型网格自适应技术来捕捉冲击波的波阵面。其中,原始的背景网格尺寸为30cm,初始时刻经过网格自适应加密后,TNT爆炸产物和水界面附近的最小网格尺寸约为1mm。整个计算区域的网格总量控制在(6~10)×104范围内,从而在捕捉激波峰值的同时,能够有效减少计算量,提高计算效率。 计算得到水下爆炸不同距离处的冲击波峰值超压和冲量,并与实验结果[18]进行了对比,如图4所示,两者符合较好。 图4 不同距离处的冲击波峰值超压和冲量Fig.4 Peak overpressures and impulses at different radii 下面计算一个浅水爆炸问题。计算区域为[1, 1]×[1, 1]m,将初始半径为0.0527m的球形TNT放置在水面下方0.2m处,在初始时刻引爆TNT炸药,计算爆炸产生的冲击波在水中和水-气界面中的传播过程。计算模型包含3种介质:TNT 爆炸产物、水和空气,同时也包含两个物质界面,即爆炸产物与空气的界面以及水与空气之间的界面。其中,TNT、水和空气分别采用 JWL、多项式和理想气体状态方程来描述。初值条件如下: 图5为计算得到的不同时刻水下爆炸冲击波压力云图。TNT爆炸后在水中产生冲击波,并同时在水中形成气泡。由于炸药距离水面较近,在t=20s左右时,冲击波先到达水面,并与自由水面发生作用,同时产生向空气中传播的透射激波和向水中传播的反射波。由于气泡附近水压很大,因此遇到反射波后会产生一个向上运动的压缩波。随着时间的演化,气泡附近的水压逐渐变得复杂,气泡的形状在膨胀过程中也逐渐变成椭球型。计算结果表明,本数值模拟方法能够对浅水爆炸等涉及多种具有高度非线性状态方程的介质间相互作用过程进行定性正确的数值模拟,为后续进一步的定量研究奠定了基础。 图5 浅水爆炸典型时刻的冲击波压力云图Fig.5 Pressure contours of shallow water explosion at typical time 计算1kg TNT在空气自由场中爆炸产生的冲击波传播过程,分别采用JWL和理想气体状态方程来描述TNT爆炸产物和空气。图6(a)、(b) 为典型时刻冲击波压力云图和相应的网格自适应图,图7为计算得到的距爆心不同距离处的冲击波峰值超压和冲量,并与相关的实测结果[19-20]进行对比,两者基本符合,验证了计算模型和计算方法的正确性。 图6 TNT空中爆炸的冲击波压力云图和自适应网格图Fig.6 Pressure contours and adaptive meshes of TNT explosion in free air at typical time 图7 不同距离处的冲击波峰值超压和冲量Fig.7 Peak overpressures and impulses at different radii 在爆炸近区,爆炸产物和冲击波尚未完全分离。由于爆轰产物的密度远高于空气,此时需要精确模拟爆炸产物与空气之间的相互作用,才能准确计算该区域内的真实载荷状态。利用本研究方法计算了1kg TNT爆炸产生的近区冲击波在遇到刚性壁面时的反射过程,得到了不同时刻的冲击波反射压力云图,如图8所示。 由图8可知,当爆炸产生的冲击波传播到刚性壁面时,首先在爆心截面发生正反射,然后沿壁面向两侧继续传播,并发生规则反射。当入射角增大到临界角附近时,冲击波进一步发生了马赫反射,最终形成比较复杂的马赫波。图9给出了计算得到的爆心截面处的冲击波正反射峰值超压和冲量,与文献[20-22]以及实测数据[23]的结果比较吻合。 图8 柱形容器内反射冲击波压力云图Fig.8 Reflective pressure contours of TNT explosion in cylindrical vessel 图9 不同距离处的正反射冲击波峰值超压和冲量Fig.9 Peak overpressures and impulses of normal reflection at different radii (1)提出了一种处理高度非线性状态方程的多介质Riemann问题的通用求解方法,能够准确、高效处理多种复杂介质间的相互作用。 (2)结合Euler坐标系下具有清晰界面的可压缩多介质流体数值方法,建立了一套能够模拟具有高密度比、高压力比以及复杂状态方程的二维多介质流体计算体系。 (3)利用强稀疏波Riemann问题和气-水多介质Riemann问题,验证了数值方法的健壮性和精度。 (4)结合并行计算和网格自适应技术,对TNT爆炸冲击波在水下、空气自由场和柱形容器内的传播过程进行了数值模拟,得到了与实测数据一致的数值结果,验证了数值方法在爆炸冲击波问题中应用的可靠性,为爆炸冲击波在复杂环境下的传播规律研究奠定了基础。3 健壮性与精度测试
3.1 Riemann问题的健壮性测试

3.2 气-水多介质Riemann问题
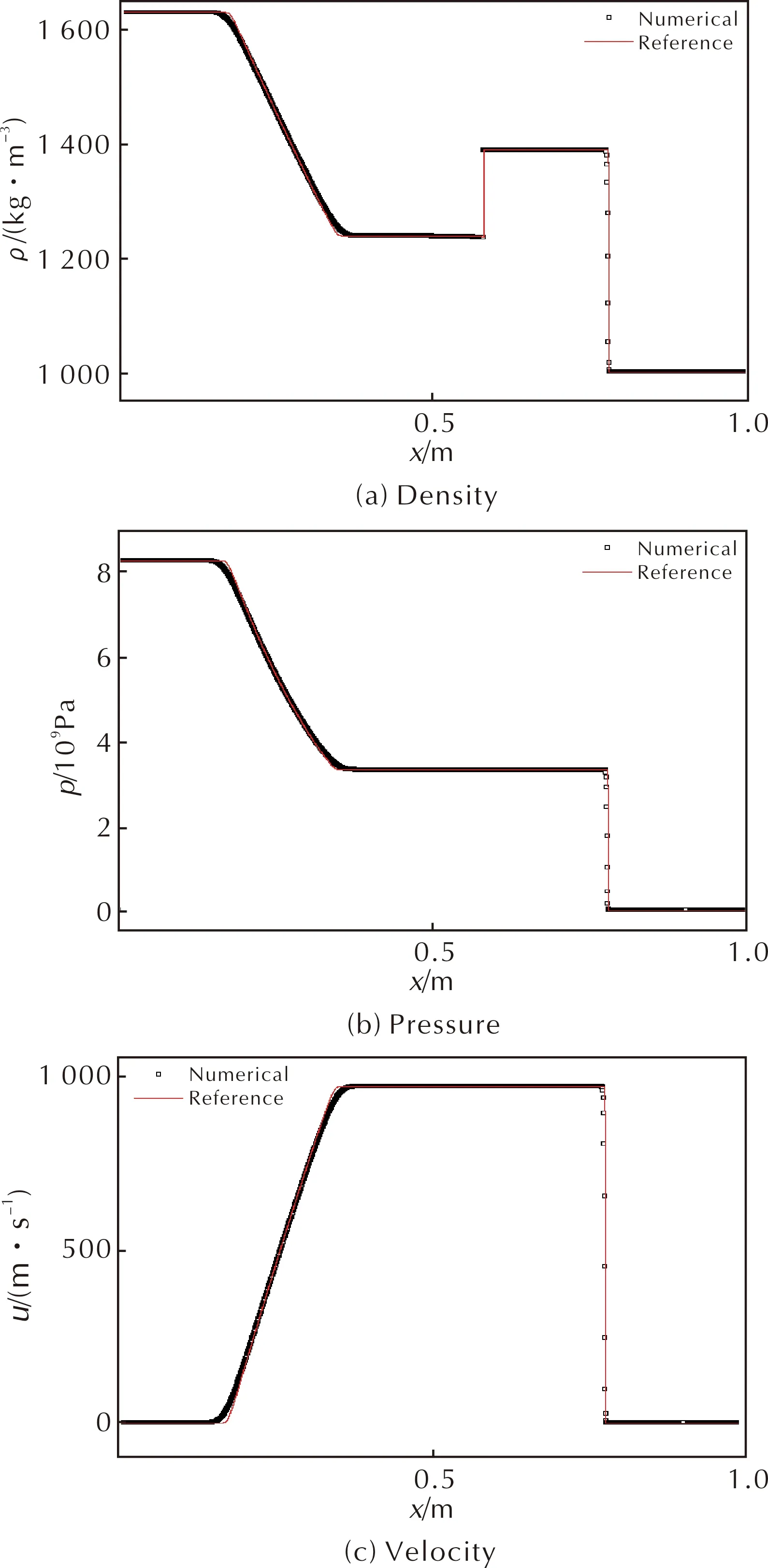
4 在爆炸冲击波计算中的应用
4.1 水下爆炸冲击波数值模拟


4.2 TNT空中爆炸自由场冲击波数值模拟
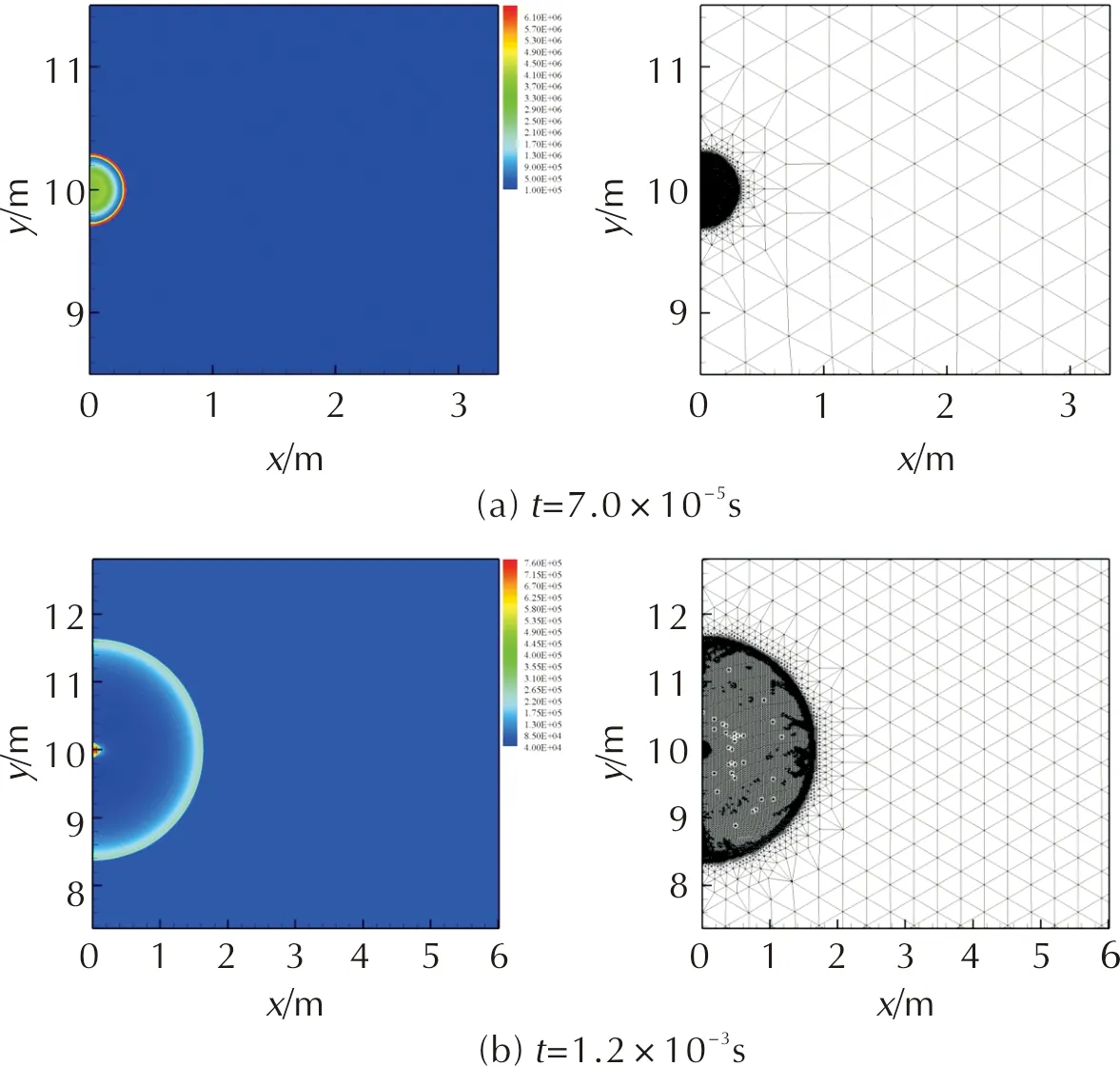
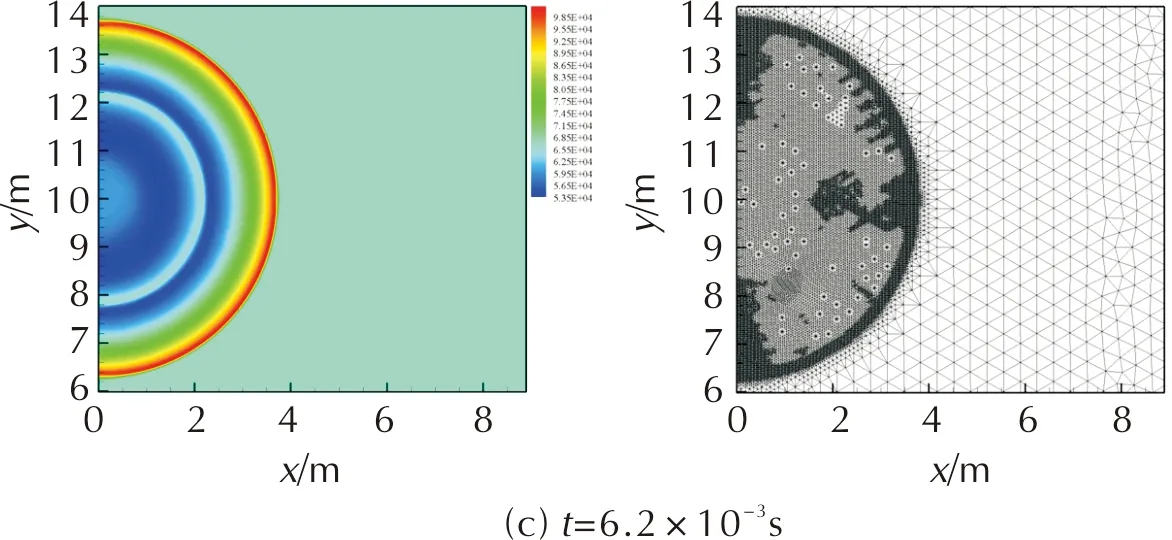

4.3 柱形容器内冲击波反射数值模拟

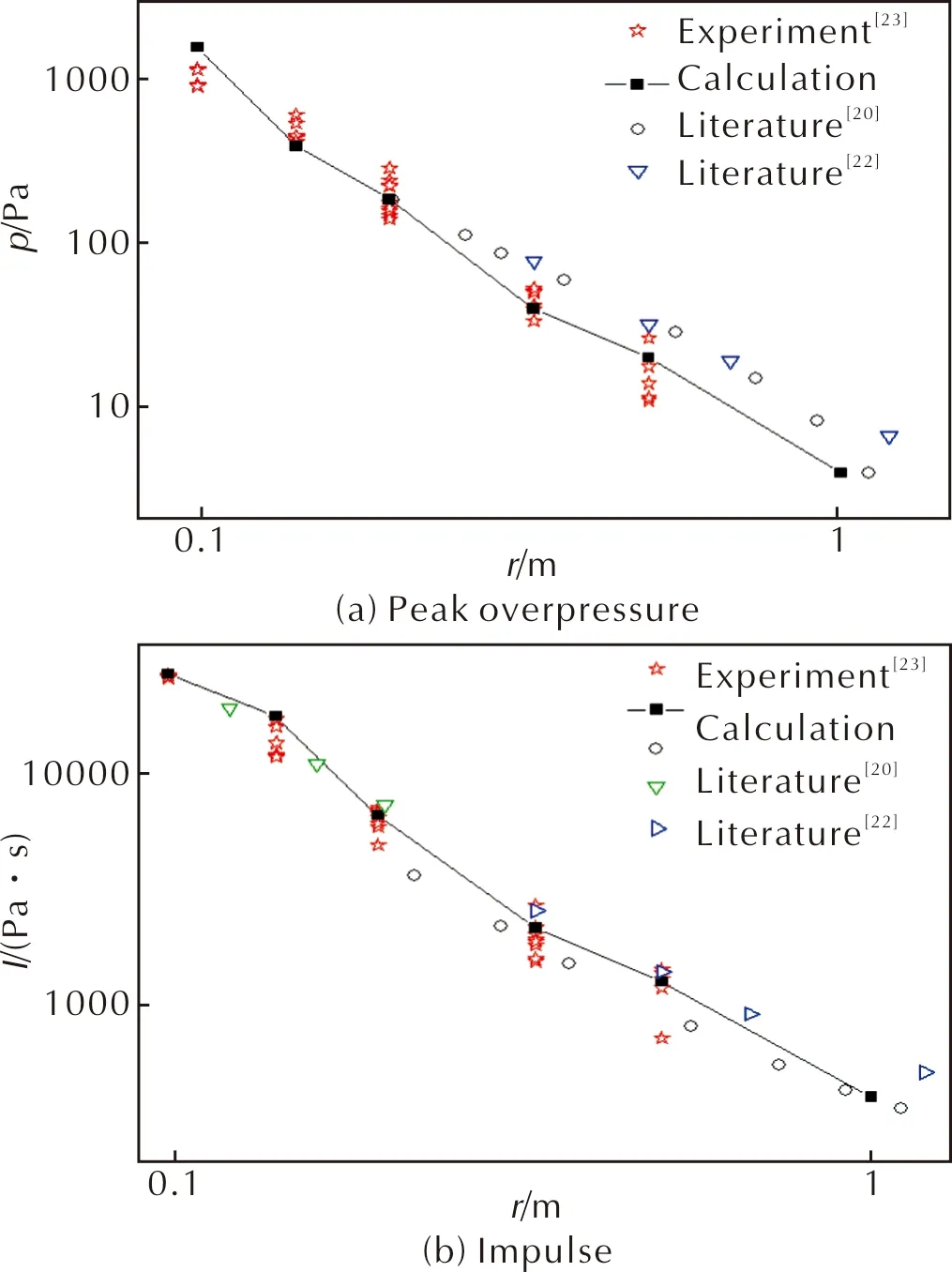
5 结 论
