水中爆炸冲击波对靶体结构的毁伤准则研究
2020-07-01王树山张静骁王传昊
王树山,张静骁,王传昊,卢 熹,马 峰
(1.北京理工大学 爆炸科学与技术国家重点实验室,北京 100081;2.沈阳理工大学 装备工程学院,辽宁 沈阳110159)
引 言
水中爆炸冲击波是造成目标毁伤的核心因素之一,其对目标结构的毁伤准则与判据是战斗部威力设计以及武器毁伤评估的重要依据[1]。水中爆炸冲击波作用下全尺寸目标结构冲击响应试验是获得对目标毁伤准则与判据最真实有效的方法,但受限于成本往往难以通过大量试验研究得出准确且实用的毁伤准则与判据。以冲击波参量(峰压、比冲量、能流密度)为毁伤准则与判据是较为常见的方法[2]。早期学者们倾向采用冲击波到达舰船时的峰压或能量密度来描述冲击环境和目标毁伤程度,即当冲击波峰压或能流密度近似相等时,目标毁伤程度也近似相等[3-4]。如早期前苏联依据峰压将舰艇破坏程度分为三级,北约国家依据能流密度将舰艇破坏程度分为十二级[3-5]。Keil[3]首次以爆炸几何位置和冲击波能流密度为变量提出了冲击因子的概念,依据试验结果论证了船板塑性变形与冲击因子间存在函数关系。随后学者们在Keil工作基础上对冲击因子的适用范围和精度进行了大量研究,提出不同修正形式的冲击因子[5-9]。可以认为,用冲击因子来评价水中目标毁伤程度和评估水中武器毁伤效能,成为过去几十年最普遍的方法。
然而,无论以单一冲击波参量或是基于能流密度参量改进的冲击因子作为水中毁伤准则与判据,都存在不可忽视的理论缺陷。相同峰压的毁伤结果因能流密度(冲击因子)或比冲量不同而不同,相同能流密度(冲击因子)或比冲量的毁伤结果因超压的不同而不同。目标的毁伤程度不仅决定于载荷峰压和比冲量的联合作用[10],甚至载荷波形都对结构响应结果有不可忽视的影响[11]。自二战起,基于P-I图的评估方法被广泛应用于评估冲击波作用下建筑结构的破坏程度[12]。利用载荷的峰压和比冲量计算结构毁伤程度的上下限,找寻当目标受到某P-I组合载荷作用时目标毁伤程度的评估方法。其中针对不同材料、不同边界[13-20],学者们给出了基于P-I图法不同载荷下结构毁伤程度的评估模型。
精准且合理的毁伤准则与判据应当综合衡量载荷压力与时间之间的关系特征。因此,本研究基于P-I图理论、量纲分析理论和爆炸相似律分析,提出了水中爆炸冲击波毁伤威力参量的一般形式,建立了冲击波参量一般形式Wn/R与结构毁伤程度间的函数关系,提出了一种通用形式C=Wn/R的毁伤准则与判据,以期为水中爆炸冲击波对结构的毁伤评估问题提供参考与依据。
1 研究方法
1.1 水中爆炸冲击波毁伤威力的表征参量
毁伤准则定义为:毁伤律函数所选取的毁伤因素威力标志参量(或导出量)的具体形式,相当于函数的自变量类型。基于毁伤律和毁伤准则的定义,将毁伤判据定义为:对应毁伤律具体函数值即一定目标毁伤概率的自变量取值或取值范围[21]。
现有水中爆炸冲击波毁伤准则与判据的形式常选取冲击波峰压、能流密度(冲击因子)、比冲量的具体表征形式[22-23]。依据量纲分析理论和爆炸相似律可知,在工程计算中凝聚态炸药水中爆炸时的冲击波峰压、比冲量和能流密度可用式(1)~式(3)表示,式中冲击波参数如表1所示[22-23]:
(1)
(2)
(3)
式中:W为药量,kg;R为爆距,m。

表1 部分炸药的冲击波相似参数[23-24]
根据式(1)~式(3)可看出,当炸药类型固定时,若不同冲击波载荷之间表达式括号内W1/3/R、W(1+β)/3β/R、W(1+γ)/3γ/R计算结果相同,则不同载荷的相应冲击波威力参量相等。因此,利用Cp、CI、CE分别对冲击波威力参量峰压、比冲量和能流密度进行表征,如式(4)~式(6)所示:
(4)
(5)
(6)
因此,水中爆炸冲击波威力参量可用通用的表达形式如式(7)进行表征:
(7)
现有水中冲击波的毁伤准则与判据形式均为式(7)的特例。峰压准则形式Cp中系数Np的取值为1/3,而比冲量准则形式CI中系数NI的取值因炸药不同在0.7左右变化,冲击因子准则形式CE中系数NE的取值同样根据炸药不同而有所变化,但工程上为简便应用系数NE通常取0.5。表2为不同炸药的Np、NI、NE的取值。
当选择Cp、CI、CE任一形式的毁伤准则与判据对目标毁伤程度进行评定时,若不同工况下相应CN值相等,则目标毁伤程度相等。然而,Cp形式毁伤准则忽略了冲击波压力的时间特性而近似准静态加载,采用CI形式毁伤准则时忽略了冲击波瞬时高压的动态效应,采用CE形式毁伤准则时忽略了压力—时间曲线的波形特征和压力、时间的数值大小,最终导致与实际毁伤结果存在一定的误差。
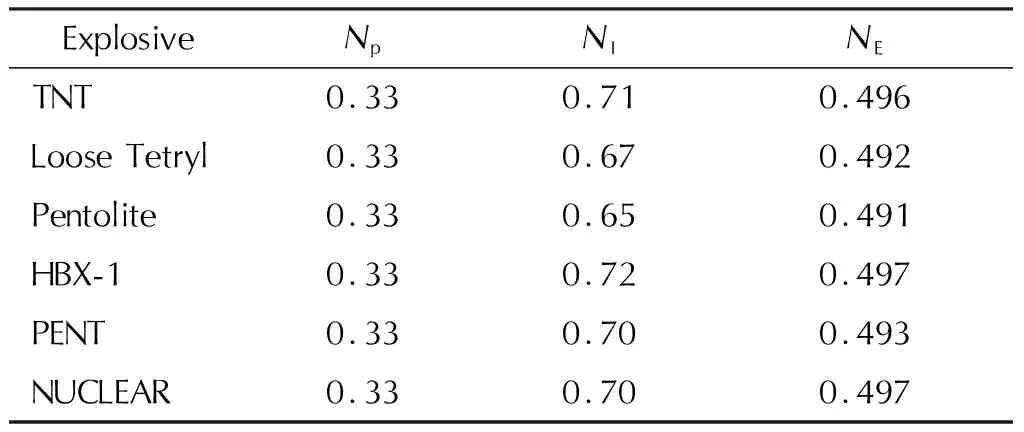
表2 部分炸药的Np、NI、NE取值
根据上述推论,本研究提出以CN=WN/R作为水中爆炸冲击波毁伤威力的通用表达式,在表征冲击波毁伤威力时表达式中系数N因脉冲载荷波形形状、压力和时间大小、目标结构特征、变形严重程度均有所变化,但取值极限不应超出峰压Np值和比冲量NI值;由于不同装药条件下NI取值不尽相同,因此N的取值范围也存在差异,如TNT装药的n值应介于0.333~0.708之间。最终水中爆炸冲击波威力参量表达式如式(8)所示:
(8)
1.2 冲击波作用下结构响应的相似性
当研究目标结构、边界约束、炸药类型和水域环境等固定不变时,改变水中爆炸冲击波载荷的强度主要通过改变药量和爆距,则目标结构的毁伤程度由药量W和爆距R决定。当使用某结构响应量X来表征目标结构的毁伤程度时,X表示为:
X=f(W,R)
(9)
由于水中爆炸毁伤问题物理过程复杂且难度大,药量W和爆距R与目标结构的毁伤程度X的高关联性难以通过相关理论解析,通过量纲分析可一定程度揭示各物理量之间的本质关系。水中爆炸冲击波载荷对目标结构造成毁伤时,影响毁伤程度表征量X的物理参量分别为:药量W,装药密度ρe,单位质量炸药化学能Qv,爆轰产物膨胀指数γ,爆距R;水初始密度ρ0,初始水静压p0,水的状态方程指数n;目标结构特征尺寸L,结构材料密度ρs,弹性模量E,泊松比υ,材料动态屈服极限σd,则:
X=f(W,ρe,Qv,γ,R,ρ0,p0,n,L,ρs,E,υ,σd)
(10)
设W、ρe、Qv为基本量,得无量纲函数关系为:
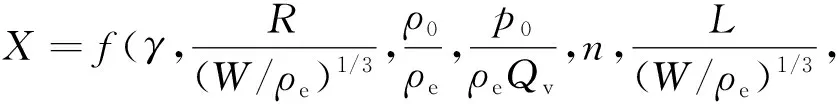
(11)
由于式(11)中仅药量W和爆距R为变量,则:
(12)
因此式(12)可简化为:
(13)
材料的应变率硬化特性导致其动态屈服极限σd不是常数,式中σd/(ρeQv)受材料本构关系影响也并不唯一。然而,确定的目标结构、特定装药量W和爆距R与材料的本构关系是唯一对应的,则相同冲击波载荷强度下结构的毁伤程度也是唯一确定的。因此在确定目标结构、装药量W和爆距R的情况下σd/(ρeQv)为常数。re=(W/ρe)1/3为装药特征尺寸,则式(13)说明目标毁伤程度X主要与比例距离R/re和L/re相关,即目标结构特征尺寸L和装药特征尺寸re的比值也影响最终结构变形的程度。式(13)可以变化为:
(14)
根据式(14)看出,当目标特征长度远大于或远小于装药半径尺寸时,此时冲击波可近似为点爆源的球形冲击波或平面波,则re/L对目标结构毁伤程度表征量X的影响可忽略不计;而当目标特征长度与装药特征尺寸相似时,目标结构在不同的冲击波形状特征下会产生不同的毁伤模式,此时不同毁伤模式下表征量X与re/L之间存在强关联性,该问题在文献中也有一定说明[9]。由于水中常见目标的特征长度通常远大于装药半径,因此本研究模型设计均忽略目标结构特征长度的影响。则式(14)近似表示为:
(15)
将式(15)与式(2)、式(3)对比发现,目标结构毁伤程度X的函数表达式形式与冲击波威力参量表达式相似,而目标毁伤程度与冲击波威力特征直接相关,则推断可以用式(16)的函数形式对目标结构毁伤程度X进行表征:
(16)
根据上述1.1、1.2节推理可知,表达式C=Wn/R既可表征爆炸冲击波威力特征,又能表征目标结构毁伤程度,以该表达式为水中爆炸冲击波的毁伤准则与判据形式具有一定可行性。其中参数n的取值决定了结构某一毁伤程度下毁伤准则的形式,不同材料、不同结构、不同边界约束条件下参数n的取值均存在一定差异,即使上述条件均相同的情况下,某目标不同的毁伤程度下参数n取值也不尽相同。当不同药量和爆距下参数C相等时,则认为目标结构的毁伤程度表征量X也相等。
1.3 冲击波毁伤准则的计算
根据前节推理论证可认为,典型的冲击波毁伤准则具有通用准则形式,即Wn/R,式中系数n的不同取值均对应一种类型的毁伤准则。据此本研究提出了一种新型的毁伤准则和判据形式,用以评估水中爆炸冲击波作用下目标结构的毁伤程度,其中关键问题在于如何通过目标结构的毁伤程度确定系数n取值。所提出的毁伤准则形式如式(17)所示:
(17)
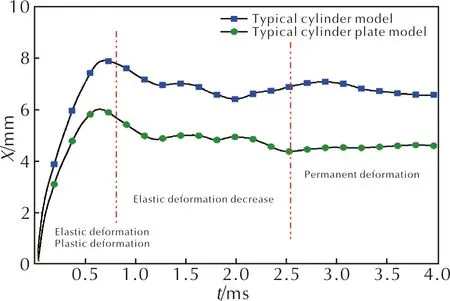
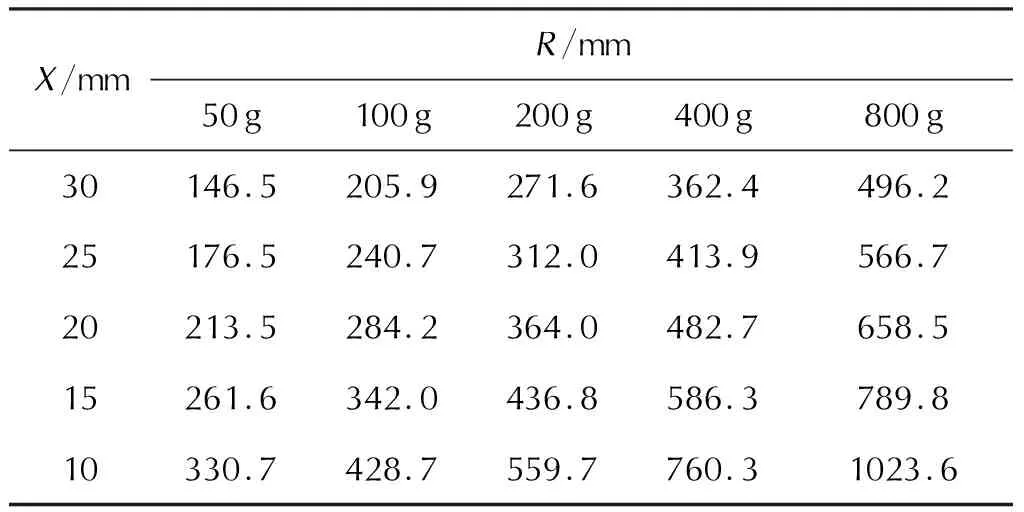
式中:Xi为目标结构所遭受毁伤程度的标志量,例如挠度、弹塑性应变等;Ci为对应毁伤程度Xi的毁伤准则与毁伤判据,计算方法如下:如式(17)所示,在选择了靶体毁伤程度表征量X之后,若假设存在若干毁伤程度X1 (18) 由式(18)推理可得: lgC=nlgW1-lgR1 lgC=nlgW2-lgR2 ⋮ lgC=nlgWn-lgRn (19) 最终通过在爆炸冲击波作用下发生相同毁伤程度的若干工况,则可计算得毁伤准则参数n: (20) 通过有限元软件AUTODYN模拟不同典型靶体在水中爆炸冲击波载荷作用下的动态响应问题,基于圆板和圆筒分别建立了有限元模型。数值模拟计算采用流固耦合算法,利用Remap方法将爆炸载荷映射进入水域。最终数值模型如图1所示。 图1 圆板结构和圆筒结构的有限元模型Fig.1 Finite element model of circular plate and cylinder 2.1.1 模型几何尺寸 圆板几何尺寸:建立了二维轴对称模型,水域大小为2000mm1000mm,网格尺寸为1mm;圆板半径300mm、厚度3mm,网格尺寸为1mm。 圆筒壳几何尺寸:建立了三维平面对称模型,水域尺寸为1000mm1000mm2400mm,网格划分采用渐变加密法,圆筒附近水域网格尺寸3mm;圆筒直径200mm、长度300mm、厚度4mm,网格尺寸为3mm。圆筒内部为空气。 2.1.2 边界条件 圆板数值计算模型中,圆板边缘设置了固支边界条件以模拟夹紧状态,模型中水域边界设置为Transmit 边界条件以模拟无限水域;圆筒壳数值计算中,圆筒壳与固定配件连接以模拟固支边界条件,模型中水域边界同样设置为Transmit边界条件。 2.1.3 数值计算模型矩阵 根据水中爆炸相似律的适用范围(7~900倍装药半径),数值计算模型矩阵选取5种药量为50、100、200、400、800g,每种药量分别对应爆距为7、10、13、16、18、20倍装药半径。 2.1.4 材料参数 材料参数来源于AUTODYN材料库和文献[24],如表3所示。 表3 数值模拟计算材料模型 水中爆炸作用下目标的变形结果并非完全由冲击波作用决定,还有滞后流冲击、气泡溃灭或气泡脉动的联合作用。而不同的载荷生成阶段、作用目标阶段、目标变形阶段均在不同的时间点,因此通过对相关物理参量关于时间的历史曲线进行分析,可获取仅冲击波载荷作用下目标的毁伤情况。需要注意的是,随着爆距的不断减小,不同毁伤因素对目标的毁伤效应耦合一起而难以分辨。因此,在分析数值模拟结果时主要通过两种方式对其他因素的毁伤效应进行区分和排除。一是通过空间尺度区分,爆距较大工况中冲击波作用下靶体结构的毁伤形式和毁伤结果不同于其他载荷;二是通过时间尺度区分,不同载荷作用下目标结构毁伤物理参量之间时间尺度不同。通过上述两种方式既可避免无法解耦毁伤效应的工况设计,又提供了数据处理的有效依据。 目标的永久变形既是水中爆炸毁伤评估中重要毁伤表征,也是水下兵器毁伤效能的设计依据。通过数值计算获得了圆板和圆筒不同工况下几何中心挠度X的变化规律,并以此作为目标毁伤表征量。典型模型的数值模拟结果如图2和图3所示。 图2 圆板和圆筒数值模拟计算结果Fig.2 Numerical simulation results of circular plate and cylinder 从图2中看出,圆板和圆筒毁伤程度较重的区域主要集中在几何中心和边界处。这是由于在冲击波作用下结构边缘产生了剪力和拉力,致使边缘处出现了大变形;结构几何中心正对应爆心而产生了应力集中,致使中心点出现了最大变形。 由图3可以看出,结构中心的变形过程大体分为3个过程:弹塑性变形同时增加至峰值、弹性变形逐渐减少、挠度不再明显变化。在结构中心永久变形稳定后,记录相应中心挠度(X)如表4和表5所示。 图3 圆板和圆筒中心挠度随时间响应曲线Fig.3 Circular plate and cylinder center deflection histories 表4 圆板结构挠度计算结果 注:D为装药和结构间距离关于装药半径的无量纲数,下同。 表5 圆筒结构挠度计算结果 根据表4、表5中心挠度X变化规律,通过线性插值和数据拟合方法寻找等毁伤情况下的不同工况,分别选择圆板和圆筒几何中心的5个典型挠度进行表征并对结果进行验证,最终获得了不同药量、圆板和圆筒等毁伤情况下的爆距如表6和表7所示。 表6 圆板结构的等毁伤条件工况 注:R为装药和结构间距离。下同。 表7 圆筒结构的等毁伤条件工况 将表6、表7结果分别绘制成对数坐标系下爆距随药量变化的等挠度曲线,如图4所示。 图4 圆板和圆筒等毁伤曲线Fig.4 Iso-damage curves of circular plate and cylinder 从图4可看出,等挠度曲线呈现良好的线性规律,且等挠度曲线间斜率相差不大,进一步证明客观存在一种表达式C=Wn/R或lgR=nlgW-lgC能够准确判断目标的毁伤程度。 根据1.3节所述计算方法对表6、表7的数值模拟结果进行计算,获得了不同靶体在水中冲击波作用下的毁伤准则与判据如表8所示。表8中毁伤准则参数n均存在一定差异,这与靶体结构、试验环境、毁伤结果、试验工况等变量均相关。因此,表8中目标不同的毁伤程度对应不同的毁伤准则,这种方式可以更精确地评价目标的毁伤程度。 表8 圆板和圆筒结构的毁伤准则与判据 注:X为结构中心的挠度变形。 将上述提出的水中冲击波作用下圆筒和圆板的毁伤准则与判据和基于单一冲击波参量的毁伤准则与判据进行比较。根据表6和表7结果,分别绘制了圆板和圆筒的毁伤曲线。其中图5为基于峰值压力、能流密度、比冲量的毁伤准则形式所绘圆板的毁伤曲线,图6为基于峰值压力、能流密度、比冲量的毁伤准则形式所绘圆筒的毁伤曲线。图中纵坐标是靶体的挠度变形,横坐标则是冲击波威力表征量Cp、CI或CE。 当水中冲击波对目标结构造成一定毁伤程度X时,其相应的毁伤判据应当唯一,即等毁伤工况计算所得Cp、CI或CE相等。从图5和图6中可以看出,相同毁伤程度的数据点均呈现离散特性,相同峰压时毁伤程度因比冲量或能流密度的不同而不同,相同比冲量或能流密度时毁伤程度因峰压的不同而不同。说明当选取单一冲击波威力表征量为毁伤准则形式时,该毁伤准则与判据无法准确表征和评估结构在水中爆炸冲击波作用下的毁伤程度。 将表8提出的毁伤准则与判据绘制成如图7所示的毁伤曲线。对比图5和图6可看出,本研究提出的毁伤准则与判据在不同毁伤程度下数值离散程度低。说明相比其他毁伤准则,本研究提出的准则在评估目标结构毁伤时误差更小、更为准确。为了量化表征不同准则的差异,给出了不同准则在评估不同靶体结构时的均方差,其中圆板结构分别在以Cp、CI、CE和本研究提出的形式为毁伤准则与判据下的标准差值为0.13、0.1、0.26、0.02,圆筒结构分别在以Cp、CI、CE和本研究提出的形式为毁伤准则与判据下的标准差值为0.11、0.14、0.31、0.04。 图5 圆板结构基于峰值压力、能流密度和比冲量准则下的毁伤曲线Fig.5 Iso-damage curve of circular plate under the damage criterion of peak pressure, energy flux density and impulse 图6 圆筒结构基于峰值压力、能流密度和比冲量准则下的毁伤曲线Fig.6 Iso-damage curve of cylinder under the damage criterion of peak pressure, energy flux density and impulse 图7 本研究毁伤准则下圆板结构和圆筒结构的毁伤曲线Fig.7 Iso-damage curves of circular plate and cylinder under damage norm of this study 由上述可知,本研究所提出的水中冲击波毁伤威力表征量和以此为表征形式的毁伤准则其本质上可视为峰压—比冲量联合准则。图8为典型的P-I图,分别由等毁伤程度曲线(或毁伤模式)、脉冲竖直渐近线和准静态水平渐近线构成。图8中曲线上任一点的毁伤程度完全相等,但造成该毁伤程度的载荷特征却未必相同。根据载荷特征的差异通常分为脉冲载荷、动态载荷和准静态载荷[25]。载荷之间没有明显界限,但两条渐近线规定了造成该毁伤程度载荷峰压和比冲量的上下限。 图8 典型P-I图Fig.8 Typical P-I diagrams 据此,依据表8的毁伤准则与判据分别绘制水中冲击波作用下圆板、圆筒的P-I图,如图9所示。曲线的绘制分别选取了毁伤程度轻(X=10mm)和毁伤程度重(X=30mm)两种典型情况。 图9 水中爆炸冲击波作用下圆板结构和圆筒结构的P-I图Fig.9 P-I diagrams of circular plate and cylinder under shock waves in water 从图9中可看出,依据本研究准则绘制的等毁伤曲线与图8中所示P-I图具有相同的曲线特征,呈现反比例函数曲线的特征且具有两条渐近线,一定程度说明本研究所提出的毁伤准则可视为峰压—比冲量联合准则;同时,将表6、表7中毁伤工况计算的峰压和比冲量标记,发现毁伤数据点与等毁伤曲线较为重合,进一步说明了数据的准确性。 然而,图9中标记的毁伤点均位于等毁伤曲线较集中的位置,这是由水中爆炸相似律和实际工况决定的。根据水中爆炸冲击波相似定律的建议,爆距的适用范围在7~900倍装药半径,对应峰压大小约为0.68~170MPa,因此图中毁伤点的纵坐标均在0~200MPa之间;同时,产生峰压大、比冲量小的冲击波其对应工况接近接触爆炸,产生峰压小、比冲量大的冲击波其对应工况接近大药量、远距离爆炸,前者本毁伤准则与判据不适用,后者试验或数值计算均存在一定困难。因此,本研究内容存在一定适用范围,且完全依据试验研究存在客观制约。 最终,根据图9(b)绘制了典型目标基于P-I图的毁伤模式如图10所示。 图10 基于P-I图的毁伤模式Fig.10 Damage mode based on P-I diagrams 由图10可以看出不同色块区域表征不同的毁伤模式和毁伤程度,依据图9(b)分为毁伤模式Ⅰ(轻度塑性变形)、毁伤模式Ⅱ(中度塑性变形)、毁伤模式 Ⅲ(重度塑性变形甚至破坏)。当不同工况计算得到的峰值压力和比冲量数据点落在某一色块时,即代表此时该典型目标受到相应色块的毁伤模式和毁伤程度。在后续工作中,可通过试验和数值计算相应证的方式进一步对上述结果进行验证。 通过本研究可以认为,水中冲击波作用下靶体结构的毁伤准则存在通用形式C=Wn/R,根据毁伤模式、毁伤程度的不同,可以获得相应的毁伤准则与判据。需要注意的是,所提出的毁伤准则与判据存在一定适用范围。首先,水下爆炸过程较为复杂,爆炸冲击波是其中最重要毁伤元素之一,但在部分情况中毁伤载荷耦合作用并且毁伤程度难以解耦,则本方法不适用于此类情况;其次本研究提出的毁伤准则形式适用于简单结构的变形破损。所提方法可以外延用于将复杂目标结构的毁伤模式如何利用结构不同形式毁伤程度的毁伤准则与判据进行耦合表征。 (1)水中爆炸冲击波峰压、能流密度(冲击因子)、比冲量等威力参量均不能独立作为毁伤准则与判据,原因在于相同峰压的毁伤结果因能流密度(冲击因子)或比冲量不同而不同,相同能流密度(冲击因子)或比冲量的毁伤结果因峰压不同而不同。 (2)水中爆炸冲击波以一般形式的威力参量Wn/R作为毁伤准则与判据,具有科学合理性以及良好的通用性和实用性。 (3)Wn/R可视为一种峰压—比冲量联合形式的毁伤准则与判据,n值因靶体、毁伤程度等的不同而不同,n的取值在0.333~Ni之间。2 有限元数值计算模型
2.1 有限元模型建模


2.2 数值计算结果




3 结果与讨论
3.1 冲击波毁伤准则与判据的计算结果分析


3.2 不同类型毁伤准则的比较


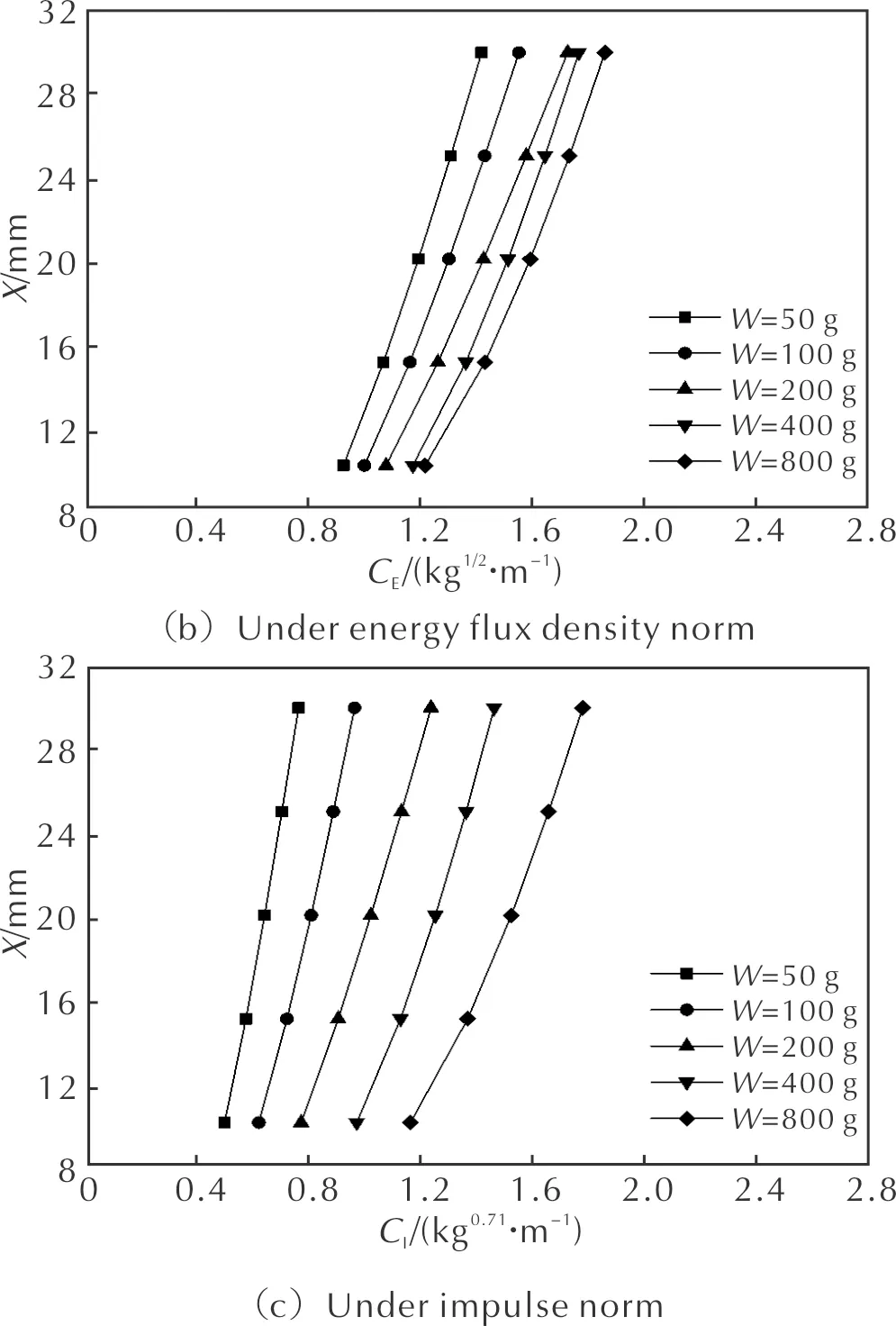

3.3 P-I图的绘制与分析

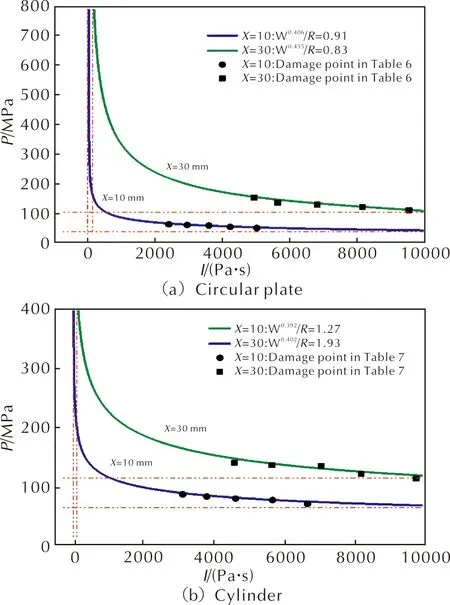
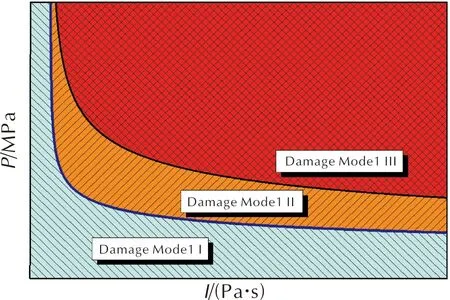
4 结 论
