两点阵列爆炸威力场分布及增益研究

冯海云，胡宏伟，肖 川，李广嘉，宋 浦

(1. 西安近代化学研究所 燃烧与爆炸技术重点实验室，陕西 西安 710065)(2. 中国兵器科学研究院，北京 100089)

引 言

阵列爆炸技术是一种特殊的爆炸能量优化控制技术，通过将若干爆炸单元按设计布局阵列布放，精确控制每个爆炸单元的起爆时序，实现爆炸毁伤元素在时间、空间维度的优化分布，显著提高爆炸能量利用率[1]。与同质量单点爆炸相比，阵列爆炸能量优化分布，有效扩大毁伤区域；其次爆炸场中毁伤特征参量的多矢量叠加，增强了局部区域或特定方向毁伤元的强度。因此阵列爆炸是摧毁各种复杂高强度防护目标的较佳袭击方式之一。

早在20世纪70年代初，美国核防局和Sandia实验室[2-4]对多弹同时和非同时爆炸的空气冲击波、地面冲击波进行了大量的试验研究和理论分析，结果显示多枚弹爆炸所形成的高压力峰值比单弹爆炸要高出3～4倍，甚至可达到8倍或更高，足以摧毁地下坚固的防护工程。

国内对于阵列爆炸的相关研究还处于探索阶段，陈志林[5]对空中两点爆炸进行了研究，认为当量相同时多点聚集爆炸造成地面破坏杀伤范围超过单点爆炸；孙百连等[6]对浅层水中沉底爆炸冲击波相互作用进行了研究，结果表明冲击波相互作用的压力叠加大大提高了爆炸威力；胡宏伟等[7]研究了多点同时爆炸时地面冲击波的聚集效应，结果表明聚焦点处的冲击波超压和冲量都大大增加。

上述研究多关注阵列爆炸对威力的提升效果，然而对于装药质量、阵列距离对爆炸威力及增益的影响并没有深入阐述。本研究开展了两点装药同时阵列爆炸冲击波威力场研究，分析了装药质量、阵列距离对两点爆炸冲击波威力及增益的影响，获得阵列爆炸冲击波作用区面积与阵列距离的关系，建立了最佳阵列距离以及两点阵列爆炸冲击波作用区面积增益的计算模型，以期为战斗部设计和防护工程设计提供理论和技术支撑。

1 计算模型

1.1 计算工况

炸药为圆柱形TNT装药，长径比为1∶1，采用中心点起爆方式，炸高h为1.5m。计算工况见表1，两点炸药装药阵列爆炸的布局如图1所示。

表1 两点炸药装药阵列爆炸的计算工况

注：2×nkg(n=1、8、27、40、51、64)表示阵列爆炸单元的数目和爆炸单元质量；L表示阵列距离。

图1 炸药装药布局图Fig.1 Layout of explosive charge

两装药同时爆炸称作两点阵列爆炸，阵列中的每个装药均称作爆炸单元，质量为M；阵列爆炸的总药量称作阵列装药总质量，用MZ表示，MZ=2M；阵列距离为两个装药中心A点和B点的直线距离，用L表示；相对应的单一爆炸单元的传统单点爆炸称作整体单点爆炸，质量用MD表示，MD=MZ=2M。

1.2 有限元模型

计算软件为大型通用显式有限元软件AUTODYN。装药位于距离地面相同高度的同一水平面上，相隔一定距离。由于模型尺寸大，网格过大会影响计算精度，尤其对于爆轰波计算结果的影响较大；网格过小，计算效率降低，计算模型建立时存在计算精度和计算效率的固有矛盾。

为了解决这个问题，计算采用二维和三维相结合的方法。模拟分析分为两部分：(1)为了能够满足所需要的误差水平，避免三维模型中网格数量过多的问题，在冲击波碰撞地面前的过程中，圆柱装药爆炸是轴对称的，冲击波传播初始阶段的计算采用二维轴对称建模。在冲击波即将碰撞地面的时刻，将计算停止，把计算结果以文件的形式保存。

(2)运用软件中的“remap”功能将二维模型中计算的最终结果状态映射到三维模型，使得计算得到继续。炸药和空气采用多物质Euler算法，建模采用mm-mg-ms单位制。

其中二维轴对称计算模型中空气域尺寸3000mm×1500mm的长方形域，网格数目为832050个。起爆点位于装药的中心，为了代表无限空气域，模型在空气边界均施加流出边界。

三维计算模型中空气域尺寸为长10m、宽2m、高2m的长方体域，网格总数为878080个。其中在下底面为刚性边界(代表地面)，其余面为流出边界。

爆轰产物的压力用JWL状态方程描述[8-9]，定义压力为比容和初始体积比容的函数：

(1)

式中：E为单位质量内能；V为比容；ω、A、B、R1、R2为常数。TNT炸药JWL状态方程参数见表2[10]。空气采用理想气体状态方程描述，参数见表3[9]。

表2 TNT炸药JWL状态方程参数

表3 空气材料参数

2 试验验证

为了验证计算模型，选用TNT装药进行试验，装药密度为1.58g/cm3，长径比为1∶1，质量为1kg。试验测量了2个炸高均为1.5m、相距4m装药同时爆炸的冲击波参数，以此验证两阵列装药同时中心起爆计算结果的正确性。试验布局如图2所示，在两装药对称中心I-1、对称轴I-2、I-3和单个装药的一侧I-4均布设传感器，测点和装药中心在同一水平面上，爆心位于装药中心。试验前对地面进行平整和压实处理。

图2 装药阵列爆炸验证试验布局Fig.2 Layout of array explosion verification test

试验采用美国压电有限公司的PCB 137自由场压力传感器捕捉超压信号。利用GENESIS数据采集仪器采集数据，采样频率为1MHz。

3 结果与讨论

3.1 计算结果与试验结果的对比

两个1kg装药阵列4m爆炸冲击波和火球碰撞高速摄影图像如图3所示。典型点处冲击波超压峰值、冲量和正压作用时间计算结果与试验值的比较见表4。

图3 阵列爆炸高速摄影图像Fig.3 High-speed photography image of array explosion

由图3可看出，两装药阵列爆炸后，二者的冲击波在装药对称面上叠加增强，可以显著增强装药对称面附近区域的冲击波压力。从表4结果也可得出，两装药阵列对称中心处的冲击波压力峰值约是爆炸单元一侧相同距离处压力的2.4倍。计算结果与试验值吻合很好，冲击波超压峰值、冲量和正压作用时间3个参数的最大误差均不大于10%。说明计算模型是合理可行的，得到的计算结果准确可靠。

表4 2个1kg装药阵列爆炸的计算结果与试验结果对比

注：Δp为冲击波超压峰值；I为冲击波冲量；t为冲击波正压作用时间。

3.2 两点阵列爆炸对称轴上冲击波超压衰减规律

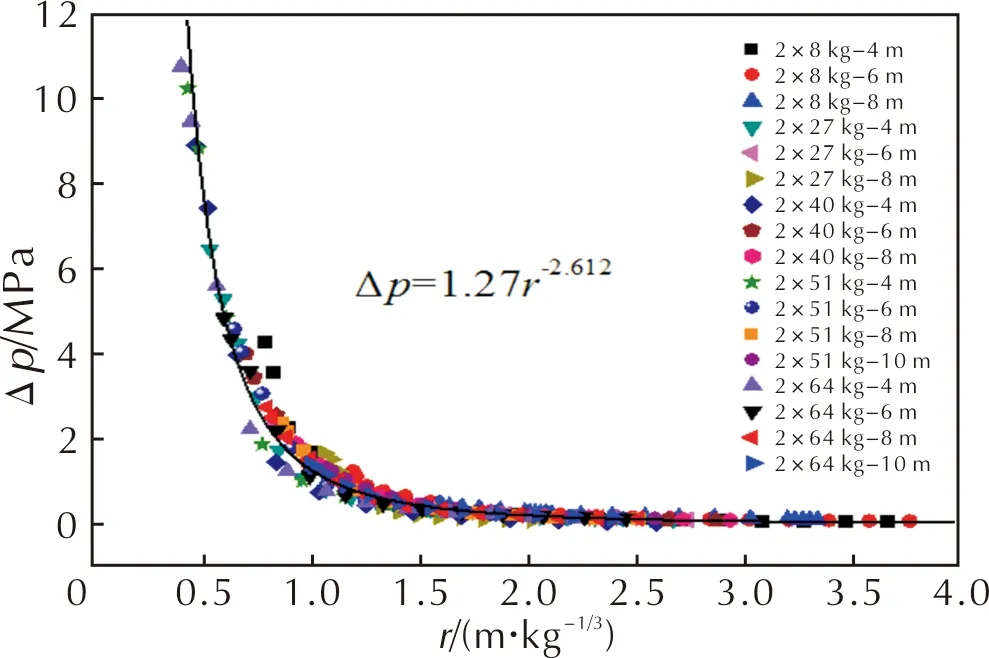
图4 两装药同时爆炸沿对称轴方向压力衰减规律Fig.4 Pressure decay law of two charges along the symmetry axis

由图4可以看出，两点阵列爆炸时，对称轴方向的超压峰值随比例距离的增大而减小，二者之间的关系符合指数衰减及相似律，表明两冲击波碰撞的合成波随比例距离的衰减与整体单点爆炸冲击波随距离的衰减规律相同。

3.3 两点阵列爆炸冲击波作用区面积与阵列距离的关系

爆炸冲击波作用区面积指以直列式阵列装药的对称中心O为原点(见图1)，由x轴、y轴和0.3MPa等值线包围而成区域的面积，如图5所示。

图5 0.3MPa冲击波作用区面积示意图Fig.5 Schematic diagram of 0.3MPa shockwave action region area

以0.3MPa的冲击波超压为毁伤阈值基准，获得了不同质量的两个阵列爆炸单元同步阵列爆炸的超压作用区面积S与阵列距离L的关系，如图6所示。

由图6可知，随着阵列距离的增大，两装药阵列爆炸的冲击波作用区面积先增大后减小。阵列爆炸单元质量在27～40kg时，较佳的阵列距离区间为6～8m；阵列爆炸单元质量在40～64kg时，较佳的阵列距离区间为6～10m。

图6 0.3MPa冲击波作用区面积与阵列距离的关系Fig.6 Relationship between the area of 0.3MPa shockwave action region and the array distance

3.4 两点阵列爆炸冲击波作用区面积增益

采用文献[8]中无限空中爆炸冲击波计算公式计算质量为2M的整体单点爆炸的冲击波，得到其0.3MPa的冲击波作用区面积，并与两个质量为M的阵列爆炸单元同时爆炸的冲击波作用区面积的计算结果进行比较，得出阵列爆炸冲击波作用区面积增益ΔS，结果见表5。

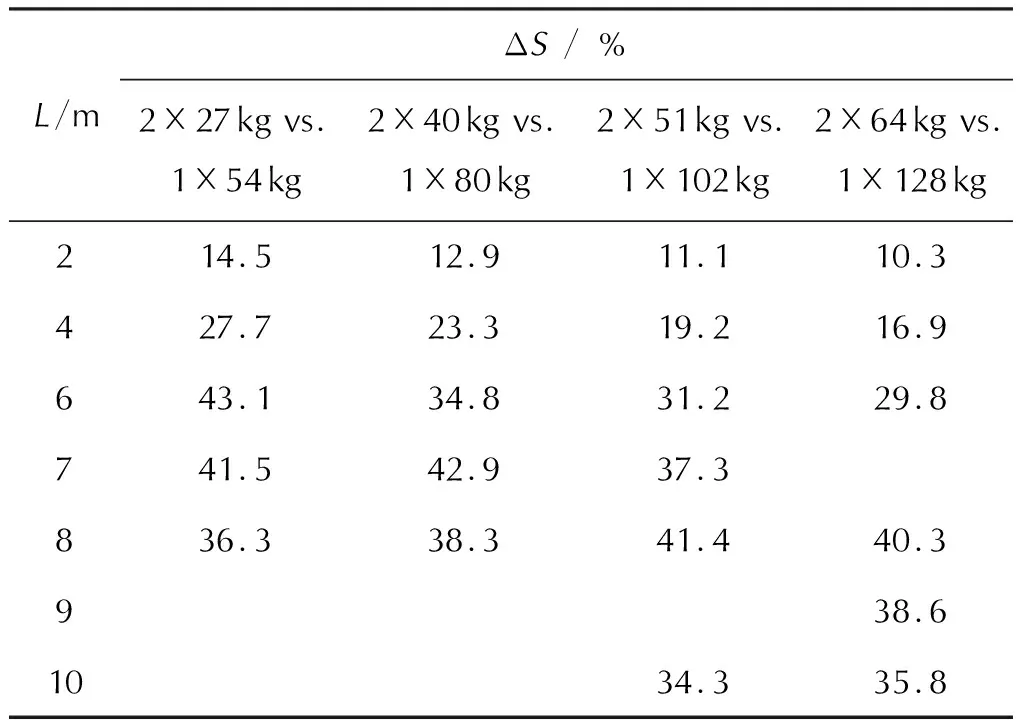
表5 两点阵列爆炸冲击波作用区面积增益结果

由表5可知，阵列爆炸单元质量在27～64kg，阵列距离4～10m范围内时，相对于同质量的整体单点爆炸作用区面积增益显著，增益大于15%，最高可达40%以上；在较佳阵列距离6～10m范围内，相对于同质量的整体单点爆炸作用区面积增益大于29%。

3.5 两点阵列爆炸最佳阵列距离的计算模型

阵列爆炸单元质量M与最佳阵列距离L的拟合关系曲线如图7所示。

图7 较佳阵列距离和阵列爆炸单元质量的关系Fig.7 Relationship between the better array distance and the explosion unit mass

由图7可知，最佳的阵列距离与阵列爆炸单元质量呈正比关系，两者的函数关系为L=2.078M1/3。

3.6 两点阵列爆炸冲击波作用区面积增益计算模型

3.6.1 计算模型

两个质量M的阵列爆炸单元同时爆炸相对于质量为2M的整体单点爆炸的冲击波作用区面积增益与阵列比例距离间的关系如图8所示，图中横坐标阵列比例距离R为阵列距离L与阵列爆炸单元质量立方根的比值。

由图8可知，两个装药阵列爆炸时，0.3MPa超压冲击波作用区面积增益和阵列比例距离的关系呈三次多项式函数关系。根据图8获得冲击波作用区面积增益的计算公式为：

图8 0.3MPa超压作用区面积增益与阵列比例距离的关系Fig.8 Relationship between the 0.3 MPa overpressure action area gain and the array proportional distance

δ=AR3+BR2+CR+D

(2)

式中：δ为超压作用区面积增益，%；R为阵列比例距离，定义为R=L/M1/3，m/kg1/3；L为阵列距离，m；M为阵列爆炸中一个爆炸单元的质量， kg；A、B、C、D由数值模拟结果拟合获得，取值分别为-12.95、51.76、-42.35、21.42。

此公式适用于阵列爆炸总质量为0～150kg的两点阵列爆炸冲击波作用区面积增益的预估。

3.6.2 计算准确性分析

利用公式(2)对不同质量两点阵列爆炸的冲击波作用区面积增益结果进行了预估，并分析了计算模型的预估精度。用公式(2)预估的结果和用AUTODYN软件计算的结果相对误差(φ)列于表6中。

表6 冲击波作用区面积增益预估结果和计算结果的对比

由表6可以看出，利用两点阵列爆炸冲击波作用区面积增益计算模型预估的结果与计算结果误差不大于15%，满足工程要求。

4 结 论

(1)数值模拟结果与试验结果吻合较好，建立的计算模型合理，方法可行，得到的计算结果可靠、可信。

(2)随着阵列距离的增大，两点阵列爆炸的冲击波作用区面积先增大后减小。最佳阵列距离与阵列爆炸单元质量呈正比关系，两者的函数关系为L=2.078M1/3。

(3)两点阵列爆炸相对于同质量整体单点爆炸，冲击波威力增益显著。在较佳阵列距离6～10m区间内，增益大于29%。

(4)两点阵列爆炸冲击波作用区面积增益和阵列比例距离呈三次多项式函数关系。增益计算模型的预估误差不大于15%。