误差为线性AR过程回归模型HD估计的弱收敛速度

徐立峰

(湖北师范大学 数学与统计学院，湖北 黄石 435002)

0 引言

考虑如下回归模型

(1)

其中yt∈R,xt=(xt,1,xt,2,…,xt,d)T∈Rd.β是d维未知参数，et是一般线性AR过程

e0=0et=atet-1+bt+ηt

(2)

其中ηt是非退化i.i.d随机噪声，Eηt=0,Dηt=σ2(σ>0)，但σ也是待估的未知参数，为保证AR过程的平稳性，我们总假定|at|<1.

模型(1)(2)包含了许多被广泛研究的模型,例如at=bt=0时，即普通的回归模型，而Maller[1],Pere[2], Hu[3]研究了at=a,bt=0的情形。

众所周知，估计量的统计性质严重地依赖于所假定的概率模型，而概率模型的正确性假定往往是脆弱的，因此考虑估计量在偏离原模型假定的条件下的“稳健性”(robustness)就成为很重要的问题.因此近50年来，具有良好稳健性的统计量不断被讨论,Huber-Dutter(HD)估计就是受到广泛关注的稳健估计之一(参见[4～8]).

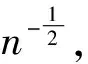
1 估计方法

(3)

其中ρ是非负凸函数，ρ(0)=0,ρ(t)/|t|→k(|t|→∞,k>0)，{An}是适当选择的正常数序列。

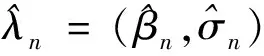
(4)

(5)

(6)

(7)

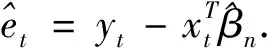
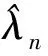
2 主要结果与证明

为得到本文的结果，我们需要引入如下条件

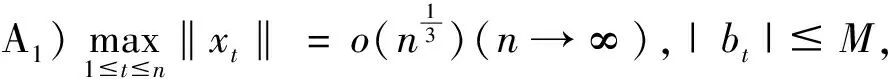
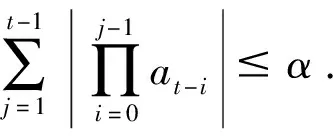
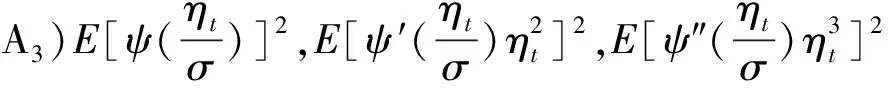
注 条件(A1)弱于[4,9,8]中对应的条件。(A2)弱于[8,10]中相应条件。而[4,8,5]用到了类似于(A3)或更强的条件。

本文主要结果如下

(8)

证明 记ξt=bt+ηt，则

(9)

由(2)迭代得

et=atet-1+ξt=at(at-1et-2+ξt-1)+ξt=atet-1et-2+atet-1+ξt

=atet-1(at-2et-3+ξt-2)+atξt-1+ξt=…

=atet-1…a3a2ξ1+atat-1…a3ξ2+atat-1…a4ξ3+…+atet-1ξt-2+atξt-1+ξt

(10)

记[atat-1…a3a2b1+atat-1…a3b2+…+atat-1bt-2+atbt-1+bt]+

[atat-1…a3a2η1+atat-1…a3η2+…+atat-1ηt-2+atηt-1+ηt]=J1+J2，则

|J1|≤{|atat-1…a3a2|+|atat-1…a3|+…+|atat-1|+|at|+1}M

(11)

由独立性和二阶矩的正交性，

由于

(12)

设Fn(λ)是Q(λ)的Hessian矩阵，即

(13)

其中*表示使Fn(λ)成为对称矩阵的元素。

经计算可得

(14)

(15)

(16)

记

(17)

其中λt=βl(l=1,2,…,d),λd+1=σ.

第二步，我们证明

(18)

由(14)，对∀i,j

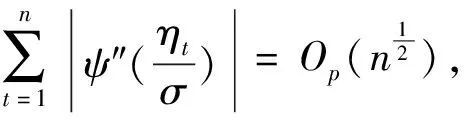
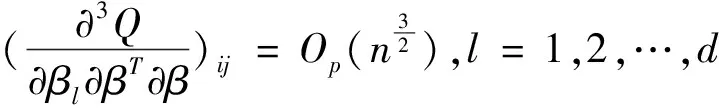
(19)

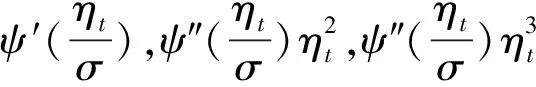
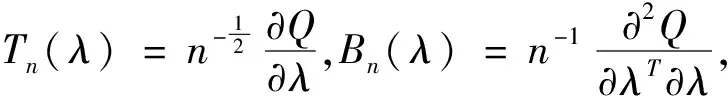
(20)

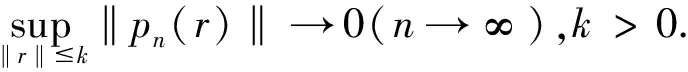
事实上，由Taylor公式

(21)

其中Rn(r,s)第l个元素为

(22)

对‖r‖≤k，有