基于快速终端滑模方法的二阶多智能体系统一致性跟踪

汪 丽，徐小林，韩 涛，吴 杰

(湖北师范大学 机电与控制工程学院，湖北 黄石 435002)

0 引言

随着智能体应用领域的不断发展，智能体面临的工作环境和任务越来越复杂多变，有些较为艰巨的工作任务对单个智能体来说很难甚至无法完成。而多智能体系统由于有更高的效率性，更低的智能体故障敏感性，更大的灵活性等特征，在执行任务时表现出更大的优势，因而，多智能体系统的研究得到各个领域研究者的密切关注，比如编队[1]、协同[2]、一致[3]等。其中，作为多智能系统问题的基础，一致性一直是一个热门问题。

多智能体的一致性是指随着时间的变化，所有个体的状态会收敛到一个相同的值。一致性问题的基本思想是构建一个分布式控制器，以确保智能体依赖于相邻智能体信息就能够达到一致。一致性问题已经从一阶多智能体[4～5]发展到二阶多智能体[6]，与一阶多智能体相比，二阶多智能体的一致性问题更加困难和复杂。因为二阶系统的一致性不仅包括一阶多智能体的位置一致性，还有速度一致性。在文献[7]中，针对含有干扰和未知速度的二阶系统，首先通过高增益观测器测定未知速度，然后介绍了基于反馈方法的控制器，使得系统在李雅普诺夫定理作用下实现了二阶有限时间一致。在文献[8]中，基于无领导者的网络通信拓扑，讨论了具有外部有界干扰的二阶多智能体的有限时间一致跟踪。根据相邻智能体的状态及速度信息，构造了一种新颖的一致控制器以实现有限时间一致性。在文献[9]中，介绍了基于EID估计器和Smith预测的控制器设计的输入时滞多智能体系统的鲁棒一致性问题，利用李雅普诺夫方法实现了系统的渐进一致。在文献[10]中，针对二阶多智能体，提出了与传统的领导跟踪方法不同的解决方案。传统的方法都是假定每个代理都满足利普希茨连续条件的固有动力学，而文献[10]研究了一种更为通用的情况：不连续的固有动力学。通过非平滑方法，首先提出了一种非线性协议，然后根据稳定性理论实现了一致性。在以上研究中，很少有人设计基于滑模方法的控制器来解决二阶一致性，而事实上，滑模控制对系统更好地控制精度、更小的状态误差。

基于以上讨论，本文研究了有向拓扑图下基于快速终端滑模方法的有限时间一致性。本文的主要贡献在：1)与文献[8]中无领导者一致性相比，本文中的领导跟随一致性可以减少系统的能量消耗，含有更好的容错功能。2)与文献[9]中的渐进一致相比较，本文采用的有限时间控制器使得系统收敛时间更快，而不是收敛时间趋于无穷。3)与文献[10]中在无向图下的多智能体系统有限时间一致性跟踪相比，本文不仅采用了快速终端滑模方法，使得系统状控制精度更好，收敛速度更快，同时将有限时间一致性拓展到了有向拓扑图，使拓扑形式更有一般性与实际性。

1 预备知识

多智能体的通信拓扑由加权图G(v,ε,A)表示，其中v=1,2,…,N和ε⊂v×v分别表示有限的非空顶点集和边集。邻接矩阵A定义为：

其中(i,j)∈ε表示第i个智能体可以接收第j个智能体的信息。另外，图G的拉普拉斯矩阵L定义为

本文中，我们考虑一组多智能体，其中包含一个领导者(标记为0)和N个跟随者(分别标记为1,2,…,N).另外，G表示跟随者之间的信息交流，H表示包括跟随者与领导者在内的所有智能体之间的信息交流。领导者与跟随者之间的信息交流定义为

其中(i,0)∈ε表示第i个智能体可以接收领导者的信息。

2 问题描述

考虑含有N+1个智能体的系统，其中含有N个跟随者，分别标记为i=1,2,…，N.一个领导者，标记为0.每个跟随者的动态系统如下所示：

(1)

其中，xi,vi,ui分别表示第i个跟随者的位置、速度及控制输入。

另外，领导者的动态系统为：

(2)

其中，x0,v0,u0分别表示领导者的位置、速度及控制输入。

这个多智能体达到有限时间一致，也就是存在一个时刻T(x(0))，使得

t≥T(x(0)),xi(t)=x0(t),vi(t)=v0(t),i=1,2,…，N.

假设1：多智能体系统的通信拓扑是一个有向生成树，并且以领导者为根节点。

3 主要成果

在本节中，我们研究多智能体系统(1)和(2)的二阶一致性。基于终端滑模控制策略，介绍了一种新的分布式跟踪控制器。分布式控制器的设计过程主要包括两个步骤。首先，我们通过测量相邻跟随者的状态及速度，引入了跟踪误差系统，从而设计了滑模面。在跟踪误差和滑模表面的基础上，介绍了每个跟随者的控制器。

定义跟踪误差如下：

在此基础上，我们为每个跟随者设计了一个滑模矢量：

si(t)=eiv(t)+ceix(t)+d(eix(t))m/q

其中，i=1,2,…,N;c,d>0；q,m(q>m)是正奇数。由此，可设计控制器如下：

(3)

根据以上讨论，下面的定理详细介绍了主要结果。

定理 假设1成立，考虑多智能体系统(1)和(2)，在控制输入(3)下，则一致性在有限时间内可以实现，其中有限时间满足

证明 为了证明这一结果，我们将使用终端滑模控制技术来解决该问题。因此，证明分为以下两个步骤。

步骤1：为验证所有滑模都可以在有限时间内实现，我们采用滑模矢量的导数：

然后，用矩阵形式表示滑模导数和控制器：

因此，跟踪误差表示为

定义李雅普诺夫函数V(t)=1/2sT(t)s(t)，可得

=-sT(t)sgn(s(t))

≤-‖s(t)‖2

根据李雅普诺夫定理，得出V(t)在有限时间内达到零的结论，则s(t)=0将在有限时间内保持。

步骤2：在以上详细分析的基础上，如果s=0，则显然

si(t)=eiv(t)+ceix(t)+d(eix(t))m/q=0,i=1,2,…,N.

显然根据快速终端滑模定理，可知状态误差与速度误差在有限时间内达到(0,0).假设1成立，则矩阵H=L+B是可逆的，则

t≥T,xi(t)=x0t,vi(t)=v0(t)

这意味着二阶多智能体在有限时间内实现了一致跟踪。证明结束。

4 数值仿真

本部分将通过一个仿真例子来证明理论结果的正确性和有效性。我们考虑一组多智能体，其中包含一个领导者(标记为0)和三个跟随者(分别标记为1,2,3)，它们之间的拓扑关系如图1所示。显然，系统间的通信拓扑是一个有向生成树，并且以领导者为根节点，即满足假设1.

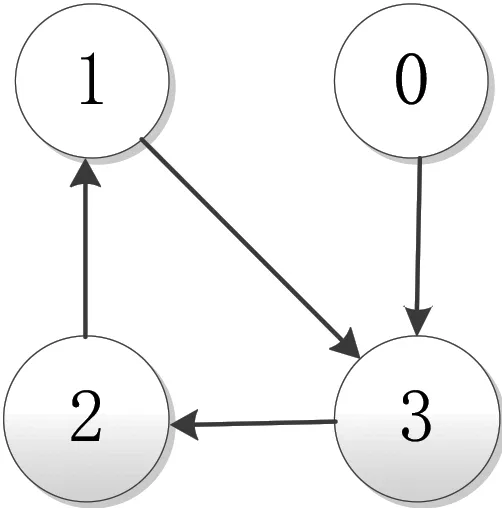
图1 通信拓扑图

设置跟随者,跟随者的初始值，领导者的控制输入分别为

x=(-7,7,9),v=(3,8,-10),x0(0)=4,v0(0)=-8,u0(t)=cos(0.1t)

参数为c=0.2,d=0.5,q=5,m=3，此外，跟随者的控制输入如(3)所示。

图2表示跟随者与领导者的位置轨迹；图3表示跟随者与领导者的速度轨迹。由图2和图3，显然可得系统实现了二阶有限时间一致。

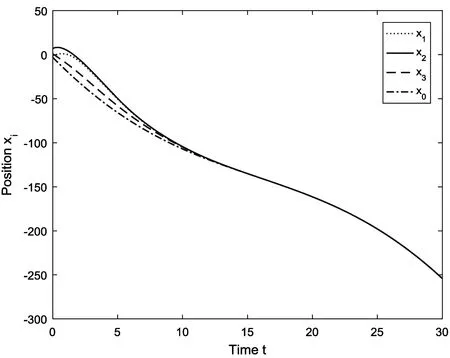
图2 位置轨迹图

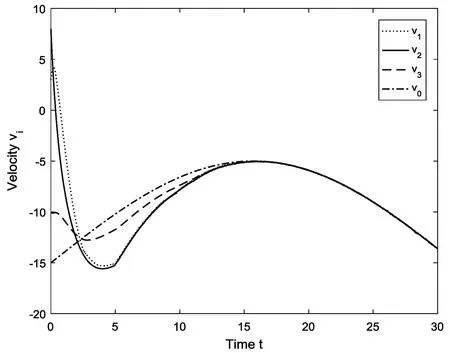
图3 速度轨迹图

5 结论

在本文中，我们研究了二阶多智能体一致跟踪问题。为了解决这个问题，我们引入了快速终端滑模方法并且在此基础上，设计了分布式一致跟踪控制器。根据李雅普诺夫定理和有限时间一致稳定理论，可以证明系统在给定的控制器下可达到一致跟踪。仿真也证实了理论结果的有效性。未来的工作将考虑带有输入饱和的二阶多智能体固定时间一致性。