变接触面液冷系统的电池模组温度一致性研究

干年妃，孙长乐，刘东旭，雷富强

（湖南大学汽车车身先进设计制造国家重点实验室，湖南长沙 410082）

伴随着全球石油短缺和环境污染的巨大压力，新能源汽车由于在节能减排和环保方面相对于传统车辆有明显的优势，近些年已呈现爆发式的增长.发展新能源汽车在全球也已成不可逆转之势，世界主要汽车生产国家纷纷制定了将全面禁售燃油车的时间表.以锂离子电池为动力源的纯电动汽车作为新能源汽车的主要发展方向之一受到了各国政府和主要汽车制造商的大力扶持和推动[1]，锂离子电池具有较高的能量密度和较长的循环寿命，是新能源汽车，尤其是纯电动汽车的理想动力源.温度对电池寿命和工作性能产生重要影响，其中最高温度和温度一致性是影响电池寿命和工作性能的最重要的两个因素[2].在充放电过程中，过高的温度会导致电池破裂、失火甚至爆炸，而在低温环境下，动力电池内部的内阻增大，电池的充放电容量急剧降低，在低温环境下使用电池，会增加电池的耗损，降低电池的使用寿命[3].因此，为了将电池温度控制在可接受范围内，并在充放电过程中保持单体间均匀的温度分布，就需要对电池进行热管理（BTM）[4].先前的学者对电池热管理方面已经做了大量的研究，包括电池单体生热模型的建立[5-8]、冷却结构的布置、冷却材料的选择等等[9-10].就目前而言，根据冷却介质，电池热管理可分为空冷、液冷、相变材料冷却和热管冷却，以及多种方式的耦合冷却.由于空气冷却的冷却性能有限，不能满足充放电倍率较大的电池系统的散热要求，而相变冷却虽然冷却性能良好，但其复杂的结构和成本限制了其在实际中的应用[11].因此，对于高充放电率、高产热率的电池组而言，液体冷却具有明显的优势[12].方形电池的液冷设计往往通过冷却板或直接浸入液体介质中来实现[13].微通道液体冷却被广泛应用到方形电池的热管理中[14-17].Qian 等人[18]研究了不同微通道数量及入口方向对电池冷却性能的影响；Xie等人[19]提出了一种Y 形微通道冷却系统；Salimpour等人[20]设计了一种环形的冷却结构，并对其进行了优化；Deng 等人[21]研究了蛇形微通道的管道数和温度一致性的关系.相对于方形电池，圆柱形电池模组液冷系统的研究相对较少.Zhao 等人[22]在充放电过程中，采用带有液体流动的波状通道对圆柱形电池模组进行冷却；胡兴军等人[23]针对圆柱形电池模组设计了8 种间接接触的液冷结构并对比了它们的冷却效果；Basu 等人[24]设计的铝片导电元件与圆柱形锂离子电池组紧密接触；Zhao 等人[25]对于42110 圆柱形电池设计了一种基于套筒的微通道液冷系统.之后Rao 等人[26]设计了一种通过改变铝块与电池接触面积来调整单体间温差的液冷系统.

根据先前学者的研究可知，圆柱形电池液冷系统主要通过改变结构形式来达到降低最高温度和温差的目的.相对于降低模组的最高温度，调节单体间温度的一致性更加困难.根据Rao 等人[26]对于改变铝块长度来实现降低电池单体间温差的研究，本文在此基础上提出了一种新的结构，将铝柱放置在18650 电池单体间的空隙中，分别研究了铝柱截面边长和铝柱的高度对电池温度的影响，并通过改变铝柱的高度和截面边长来增加与电池单体的接触面梯度以降低温差，并研究了不同放电倍率下单体的温差，为进一步提高电池热管理系统的工作性能提供参考和指导.

1 模型与方法

1.1 单体模型

电池单体采用松下NCR18650PF，最大容量为2 900 mA·h，标称电压为3.7 V.锂离子电池因其不同的长度尺度和几何复杂性，各层在层法向的尺寸通常为数十微米，但在电池片方向达数十厘米，且电池内部为螺旋绕制结构，所以电池单体三维模型的建立较为复杂.但是就锂离子电池的传热过程而言，只存在一个不同方向的传热速率的差异，因此可以将电池三维模型中的活性电池材料简化成具有各向异性导热特征的均质材料.为了方便仿真，采用快速仿真的电化学-热耦合模型，其耦合过程如图1 所示.一维单电池模型用于对电池化学性质进行建模以及计算电化学模型的产热，并将热量耦合至三维模型，三维模型用于对温度进行建模，并将温度耦合至一维模型.此模型大大减少了计算时间，适用于研究电池包热管理.

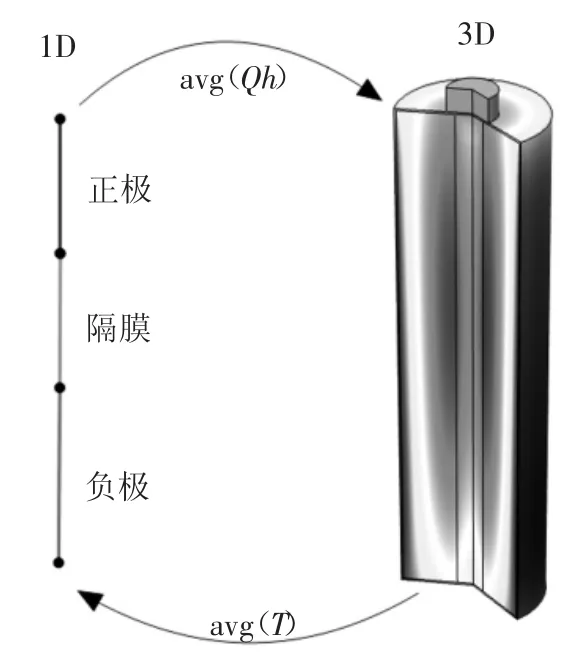
图1 电池单体电化学耦合结构图Fig.1 Electrochemical coupling structure of single battery

1.2 冷却系统结构

图2 展示了电池模块液冷散热系统的示意图，电池模块共由21 个18650 电池单体组成，沿x 方向有3 个单体，沿y 方向有7 个单体，单体间的间距都为1 mm.铝柱放置在4 个单体形成的空隙中，铝柱与单体的接触面均为单体的弧形状态，如图2（c）所示，铝柱截面形状为一个正方形减去单体弧形所占的面积，将正方形边长a 记为铝柱的截面边长，铝柱的高度记为h，管道分布如图2（b）所示，管道竖直通过铝柱，管道直径为3 mm.为节省空间，提高铝柱质量，最外侧的4 个铝柱侧边与管道中心的距离定为2 mm.此模型具有对称性，且由于中间一列单体两侧都布置有铝柱，所以外侧两列单体更具有参考性，如图2（c）所示，将外侧一列单体标号为1～7，以便于后续的研究.考虑导热系数和黏度，采用液态水作为冷却介质.电池、铝柱和冷却液的热物理性质见表1.

图2 冷却系统结构图Fig.2 Cooling system structure diagram

表1 材料热物理参数Tab.1 Thermal physical parameters of materials

1.3 平衡方程

锂离子电池生热量包括副反应热、反应热、极化热和焦耳热.由于过充和过放、电解质分解及自放电产生的副反应热几乎为零[27]，故只考虑剩下的三部分热量.在进行充放电时，锂离子和电子发生嵌入和脱嵌，运动过程中产生热量如式（1）所示，两者遵循电荷守恒定律.反应热Q1为：

式中：As为活性比面积，m2/g；iloc为局部电流密度，A/m；η 为过电压，V.

在电池的可逆反应中，理论上反应热大小相等、符号相反，但根据熵增原理，在实际进行充放电时会有极化反应产生的极化热Q2，如式（2）所示.

式中：U 为电压，V；T 为温度，K.

在充放电过程中电池内阻产生的焦耳热Q3，分为固相电子电阻和液相离子电阻产生固相欧姆热和液相欧姆热.

式中：il、is分别为固相电子电流和液相电子电流，A；Rl、Rs分别为固相电子电阻和液相电子电阻，Ω.

对于圆柱型锂离子电池，在柱坐标下的导热微分方程为[28]：

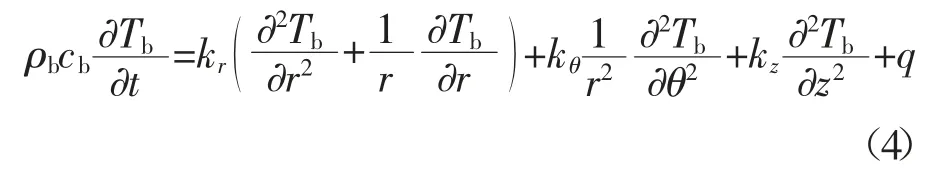
式中：ρb为电池的密度，kg/m3；cb为电池的比热容，J/（kg·K）；Tb为电池的温度；q 为单位体积产热率，W/m3；kr、kθ、kz分别为电池径向、周向和轴向的导热系数，W/（m·K）.

由于电池结构可视为多个单电池螺旋缠绕而成，其θ 向和z 向的导热系数基本相同，因此，模型（4）可简化为：

电池径向导热系数kr可根据以下公式计算[27]：

式中：Li为不同电池层厚度；ki为不同电池层导热系数.

电池轴向导热系数的计算依据为[27]：

同样地，活性电池材料的密度和比热容的计算依据为[27]：

式中：ρi、ci分别为不同电池层的密度和比热容.

冷却液使用液态水，水的能量守恒方程为：

式中：ρw、cw、Tw、kw分别为冷却液的密度、比热容、温度和导热系数；v 为速度矢量.

不可压缩液态水的运动由质量守恒方程和动量守恒方程控制：

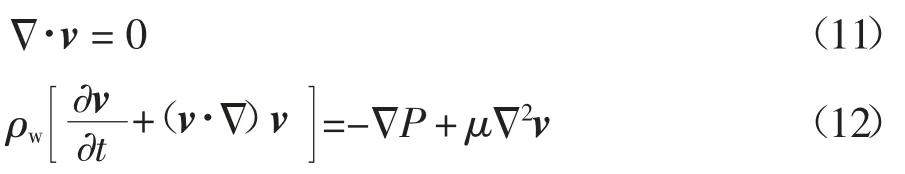
式中：P 为压强，Pa；μ 为动力黏度，Pa·s.

1.4 边界条件与网格验证

根据冷却液的性质、管道直径及入口流速，可计算雷诺数来确定是采用层流模型还是湍流模型.本文最大入口流速为0.2 m/s，雷诺数为671.36，由此可知，本文采用层流模型.在所有仿真中，入口冷却液温度、电池模组初始温度及环境温度均设为25 ℃.冷却液的入口边界条件采用速度边界条件，具体速度值在仿真过程中确定；出口边界条件采用压力边界条件，法向压力设置为0.电池模块外层有保持架、集流片、固定架等覆盖件，且整个电池包也由外壳所包覆，电池单体、冷却通道和铝块的对流传热系数设为2 W/（m2·K）.

根据牛顿冷却定律，锂离子电池热模型的边界条件用式（13）来描述：

式中：φ 为热流密度，J/（m2·s）；ha为对流传热系数；Ta为周围环境的温度.

利用有限元软件COMSOL 求解耦合传热问题，COMSOL 具有强大的多物理场耦合功能.由于控制方程的高度非线性和模型中几何尺度的不同，计算精度和计算时间依赖于网格和求解器.模型都采用自由四面体网格，以管道出口边界的温度为参考，测试了几种网格密度对其影响，以保证解的网格无关性.

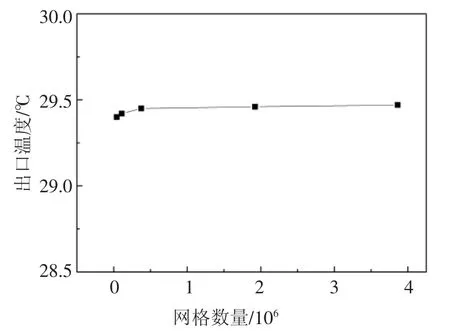
图3 网格独立性测试Fig.3 Grid independence tests

图3 显示了网格数量对仿真结果的影响，当网格数量从375 734 增加到3 862 598 时，网格数量增加了近10 倍，但仿真结果误差保持在0.03%以内，因此网格数量采用375 734 个.

2 结果与讨论

由于电池的热量都是通过铝柱传递到冷却管道，因此铝柱和电池单体的接触面积与冷却性能有很大的关系.铝柱与电池的接触面积可以通过改变铝柱的截面大小和铝柱的高度来进行调节.在接下来的研究中，我们将分别讨论铝柱截面大小和铝柱高度这两个变量对电池冷却性能的影响.

2.1 铝柱截面大小对温度的影响

选定铝柱高度为定值40 mm，只改变截面边长以达到改变与电池接触面积大小的目的，截面边长a 以1 mm 的间距从7 mm 变化至14 mm；冷却液入口流速分别设置为0.05、0.10、0.15 和0.20 m/s，电池以3 C 倍率放电至终止电压，放电时长为1 200 s.放电结束后整个电池模块的最高温度和最大温差如图4 所示.

图4 不同截面边长下的电池模组最高温度和最大温差Fig.4 Maximum temperature and maximum temperature difference of the module under different section length

由图4 可知，冷却液入口流速对温度影响显著，流速越快，最高温度及最大温差越低.随着入口流速从0.05 m/s 增加到0.20 m/s，铝柱截面边长为7～14 mm 的电池模组最高温度降低了4.72～5.69 ℃；最大温差从7.17～9.16 ℃全都降低到5 ℃以内.铝柱截面大小对温度同样也有所影响，截面越大，最高温度及最大温差越低.随着截面边长从7 mm 增加到14 mm，在流速分别为0.05、0.10、0.15 和0.20 m/s 下模块的最高温度分别降低1.97、1.41、1.14 和0.99 ℃，最大温差分别降低1.99、1.36、1.09 和0.95 ℃.

过高的入口流速虽然能有效降低电池的温度和温差，但会造成水泵更高的功率损耗.图5 是入口流速为0.10 m/s 时，在不同铝柱截面边长下1～7 号电池单体的最高温度分布.

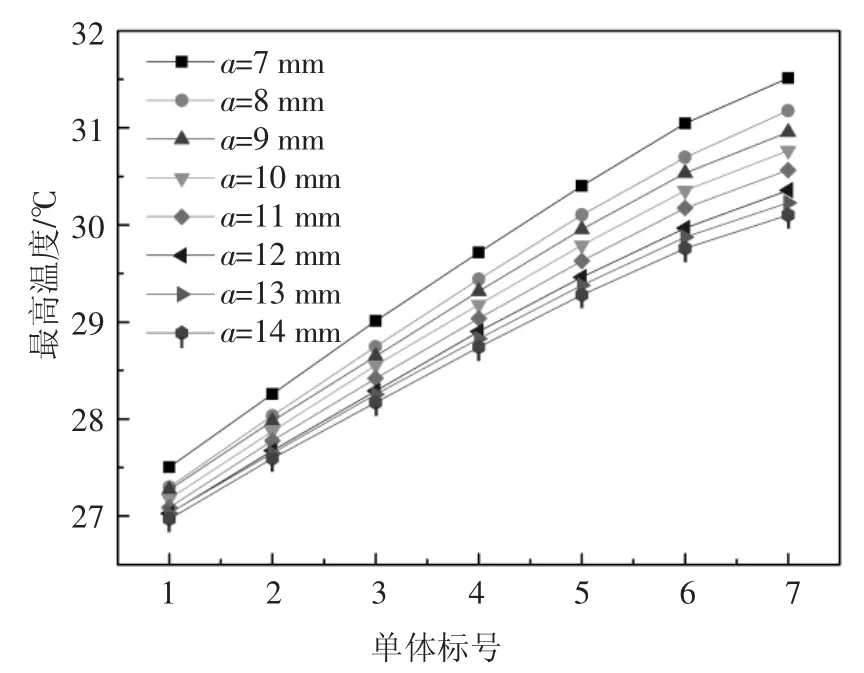
图5 不同铝柱截面边长下的单体最高温度分布Fig.5 Distribution of maximum temperature among cells at different sections length of aluminum column

由图5 可以看出，离管道入口越近的单体温度越低，且存在一个明显的梯度变化，通过调整铝柱与单体的接触面积来缓和这种梯度变化，调整接触面积的方法为调整铝柱截面边长.每个铝柱的截面边长a 由边长梯度因子α 确定：

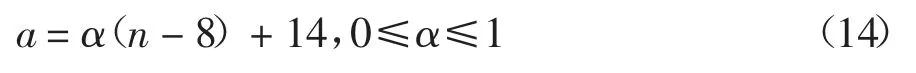
n 为电池单体的标号，由于铝柱截面边长的调整范围是7～14 mm，过小的边长会导致铝柱与单体无法接触，过大的边长则会影响周围铝柱的安装，因此α 的选择范围为0～1.选择α=0、α=0.5 及α=1 时的冷却系统进行对比.在不同α 下，冷却系统的结构如图6 所示.

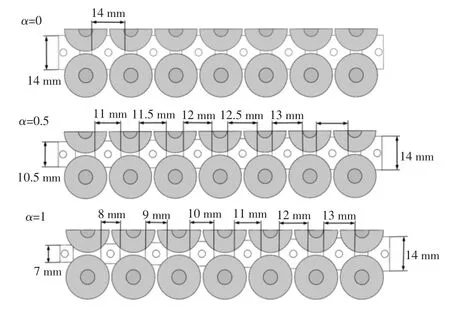
图6 不同α 时的冷却系统结构Fig.6 Cooling system structure of different α

图7 分别显示了α=0、α=0.5 及α=1 的情况下，电池以3 C 放电倍率放电至终止电压后的温度云图.在不同边长梯度因子α 下的电池模组最高温度都出现模组外侧的离出口最近的两个电池单体表面，最低温度出现在模组中间一列离管道入口最近的电池单体表面，当α 从0 增加到1 时，电池模组离管道入口较近的单体温度有所上升，其温度一致性表现更好.

图8 为α=0、α=0.5 及α=1 时1～7 号单体的最高温度曲线.由图8 可见，当截面边长梯度增大时，离管道入口越近的单体最高温度呈现上升趋势，当α=1 时单体间的最高温度差相比于α=0 时下降了0.45 ℃.可得出结论，改变铝柱截面大小对改善单体间温差有一定的影响，但由于截面边长的调整范围有限，导致这种影响并不显著.因此还需要用其他方式去缓解温度梯度.

图7 不同α 的电池模组温度场分布Fig.7 Temperature field distribution of battery module in different α

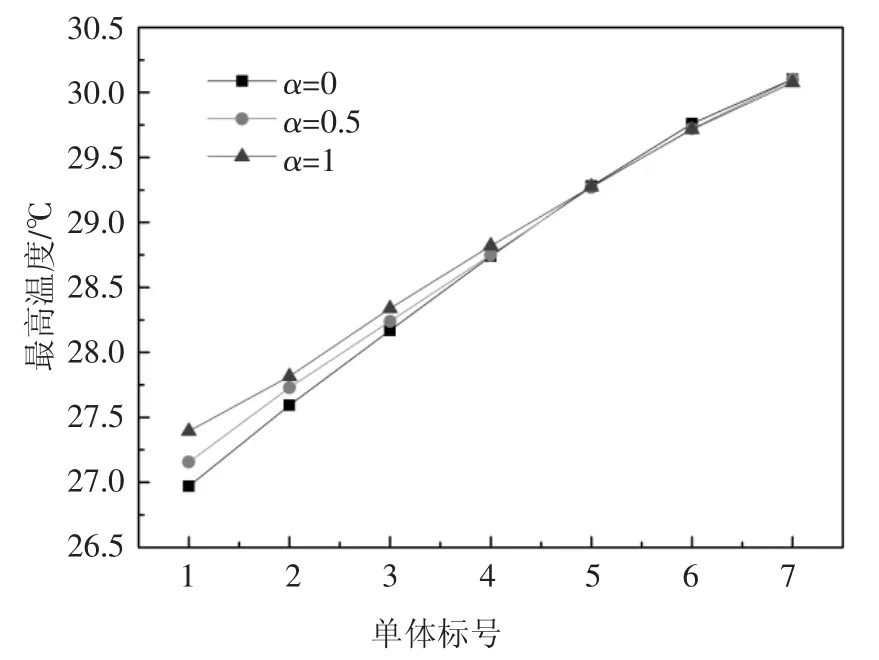
图8 不同α 的单体间最高温度分布图Fig.8 Distribution of maximum temperature between cells under different α

2.2 铝柱高度对温度的影响研究

选定铝柱截面边长为定值10 mm，铝柱高度以5 mm 为间隔从20 mm 变化至60 mm；冷却液入口流速分别设为0.05、0.10、0.15 和0.20 m/s，电池以3 C 倍率放电至终止电压，放电时长为1 200 s.放电结束后整个模块的最高温度和最大温差分别如图9 所示.由图9 可见，在不同铝柱高度下，冷却液的入口流速依然是对温度影响最大的因素，随着入口流速从0.05 m/s 增加到0.20 m/s，铝柱高度为20～60 mm 的电池模组最高温度降低了4.67～5.71 ℃；最大温差从7.33～9.29 ℃全都降低到5 ℃以内.铝柱高度对温度同样也有所影响，铝柱越高，最高温度及最大温差越低.随着铝柱高度从20 mm 增加到60 mm，在流速分别为0.05、0.10、0.15 和0.20 m/s 下模块的最高温度分别降低2.51、2.03、1.72 和1.56 ℃，最大温差分别降低1.96、1.78、1.56 和1.44 ℃.

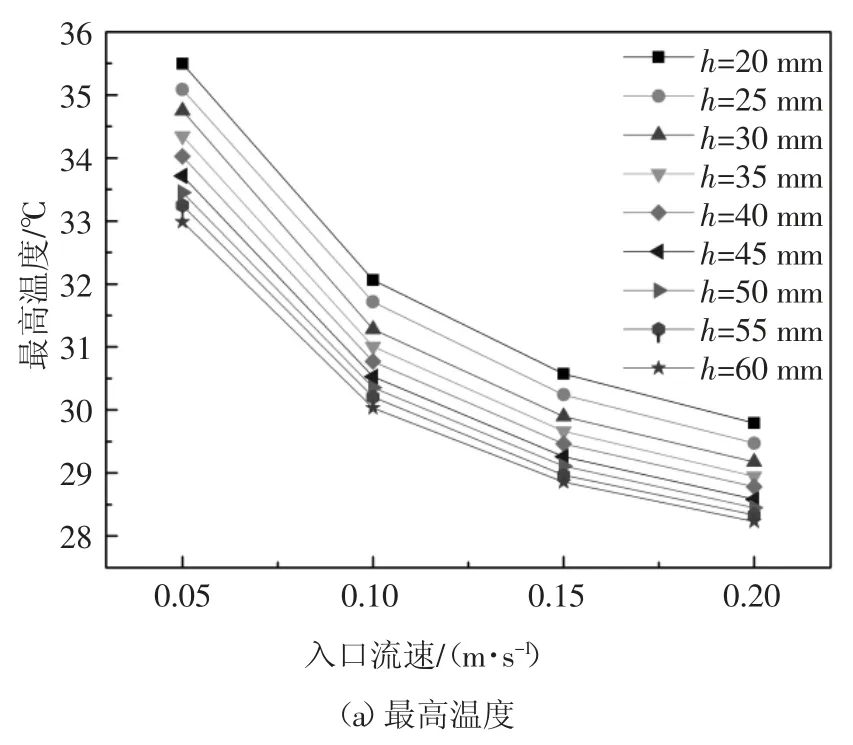
图9 不同铝柱高度下的模块最高温度和最大温差Fig.9 Maximum temperature and maximum temperature difference of the module at different height of aluminum column

同样地，为避免过高的泵功率，只观察入口流速为0.10 m/s 时的电池单体最高温度分布.图10 为在不同铝柱高度下1～7 号单体的最高温度分布.

图10 不同铝柱高度下的单体最高温度分布Fig.10 Distribution of maximum temperature among cells at different heights of aluminum column

在不同铝柱高度的情况下，离管道入口越近的单体温度同样越低，且存在一个明显的梯度变化，通过调整铝柱与单体的接触面积来缓和这种梯度变化.调整接触面积的方式为调整铝柱高度，每个铝柱高度h 由高度梯度因子β 确定：

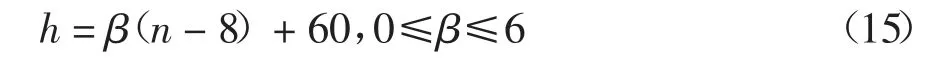
由于管道结构的限制，铝柱高度最高为60 mm，如果铝柱过短，会造成单体两端温度过高，因此高度梯度因子β 的取值范围为0 ≤β ≤6.图11 为β=0、β=4、β=5 以及β=6 时的冷却系统结构及温度分布云图.在不同高度梯度因子β 下的电池模组最高温度都出现在模组外侧两列离出口最近的两个电池单体表面，最低温度出现在模组中间一列离管道入口最近的电池单体表面，但相比于β=0，β 逐渐从4 增加到6 时，铝柱高度梯度越大，离管道入口越近的单体温度上升越明显，而离管道出口相近的单体温度有略微下降的趋势.当β=6 时，高度梯度最大，模组的温度一致性表现最好.

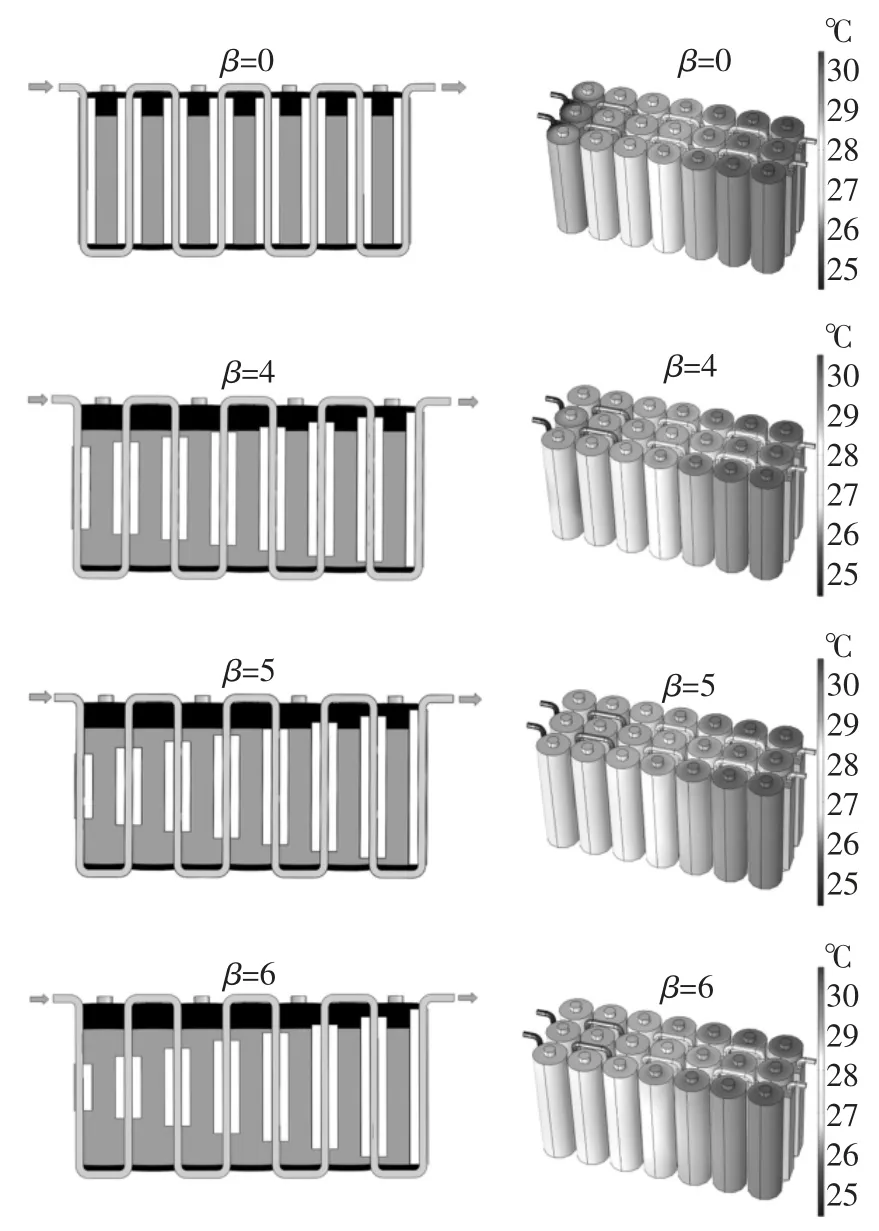
图11 不同高度梯度下的冷却系统结构与温度云图Fig.11 Cooling system structure and temperature cloud diagram at different height gradients

图12 为β=0、β=4、β=5 以及β=6 时1～7 号单体最高温度分布点线图.通过图12 可以看出，梯度因子越大，离管道入口越近的单体温度上升越明显，整个曲线表现得愈平缓.当β=0、β=4、β=5 以及β=6 时1～7 号单体最高温度差分别为3.17、2.59、2.24 和1.78 ℃；相比于β=0，当β=4、β=5 和β=6 时，单体最高温度差分别降低0.58、0.93 和1.39 ℃.可得出结论，在相对较低的入口速度下，通过调节铝柱高度的梯度可以有效缓和单体间的温度差异.

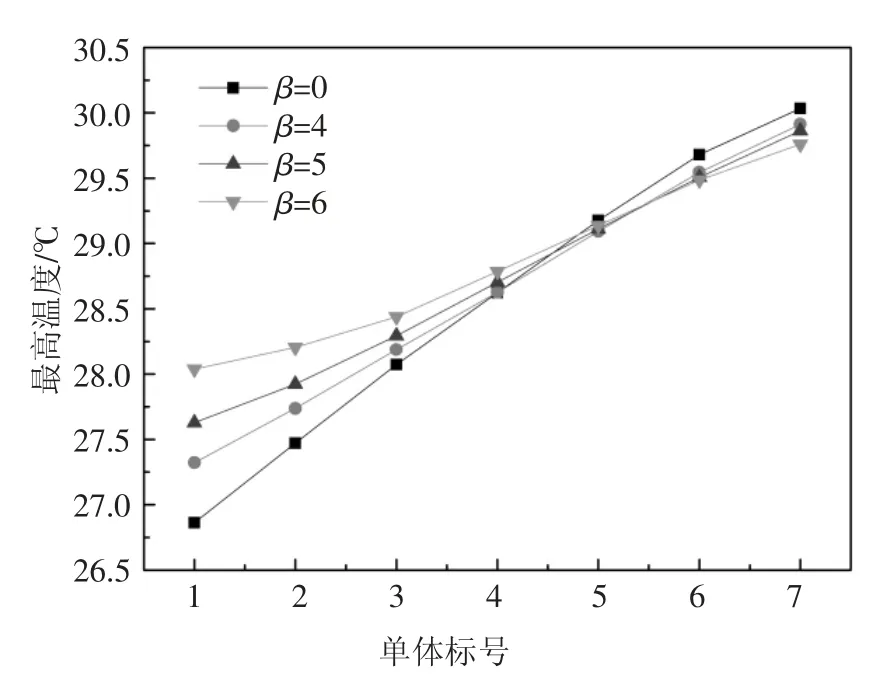
图12 不同高度梯度下的单体间最高温度分布Fig.12 Distribution of maximum temperature among cells at different height gradients

2.3 铝柱高度与截面的组合方式对温度的影响

由于对铝柱截面边长和高度的单一参数调整并不能得到单体间足够小的温度梯度，为了使铝柱与电池单体的接触面积梯度足够大，采用铝柱高度与截面的组合方法对模块温度进行研究，取最大截面边长梯度因子为α=1，取最大高度梯度因子β=6，这样可以使铝柱的电池单体的接触面积梯度达到最大.图13 为铝柱高度与截面的组合方式下的冷却系统结构图及温度分布云图.由图13 可见，铝柱与电池的接触面积梯度已经达到最大，单体间温度分布也较为均匀.

图13 铝柱高度与截面的组合方式下的冷却系统结构图和温度分布云图Fig.13 Cooling system structure diagram and temperature distribution cloud diagram under the combination of aluminum column height and section

图14 显示的是当取最大截面边长梯度因子α=1、最大高度梯度因子β=6 时与截面边长取定值14 mm、高度取定值60 mm 时1～7 号电池单体最高温度对比图.可以看出，当截面边长梯度因子α=1 与高度梯度因子β=6 组合时，曲线较为平缓，相比于铝柱截面边长和高度为定值时1～7 单体最高温度差降低1.83 ℃，整个模组的最大温差仅为3.72 ℃.

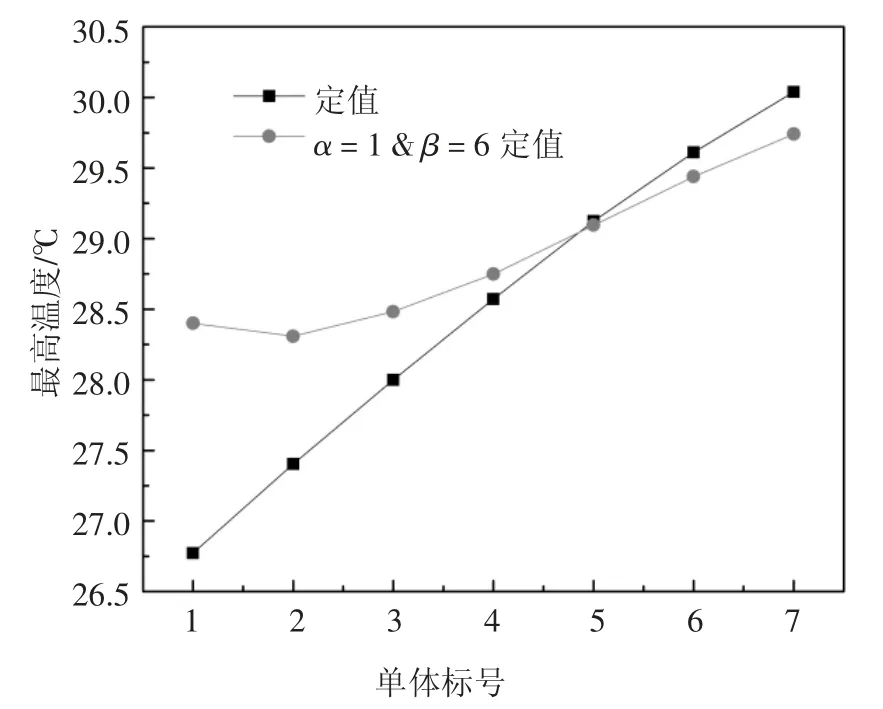
图14 定截面边长、定高度与组合方式下的单体间最高温度分布图Fig.14 Distribution diagram of maximum temperature among cells under fixed section length，fixed height and combination mode

2.4 不同放电倍率下的温度分布研究

由于前文中的模型只是针对放电倍率为3 C 的极限工况而言的，此模型在中低放电倍率下的温度分布一致性仍需要观察.利用前文中的模型，观察放电倍率分别为0.5 C、1 C 和2 C 下的温度分布.图15为不同放电倍率下模组的温度云图及单体最高温度分布图.

在0.5 C 放电倍率下，电池模组的最高温度为25.33 ℃，最大温差为0.31 ℃；在1 C 放电倍率下，电池模组的最高温度为25.87 ℃，最大温差为0.82 ℃；在2 C 放电倍率下，电池模组的最高温度为27.48℃，最大温差为2.05 ℃；在0.5 C 和1 C 放电倍率下，1～7 号电池单体的最高温度曲线表现较为平缓，在2 C 放电倍率下，曲线表现出上升的趋势，但也在较小的区间内，说明此模型能够有效调节单体间的温差分布.

图15 不同放电倍率下模组的温度云图与单体最高温度分布图Fig.15 Distribution diagram of maximum temperature between module and cell under different discharge ratios

3 结论

本文设计了一种在圆柱形锂离子电池间隙中填充铝柱的液冷热管理系统，并对系统的散热性能进行了讨论.研究了铝柱截面边长和铝柱高度对电池模块散热性能的影响.针对冷却系统，首先选定一个铝柱的高度为定值，通过改变铝柱的截面边长大小来观察系统的散热性能.结果表明，随着截面边长的增大，电池模块的最高温度和最大温差均减小.为改善温度分布的一致性，采用变截面边长来缓和单体间的温度梯度.当α=1 时，单体间的最高温度差降低了0.45 ℃.之后选定一个铝柱的截面边长为定值，通过改变铝柱的高度来观察系统的散热性能.结果显示，随着铝柱高度的增加，电池模块的最高温度及最大温差均减小，但仍存在一个温度梯度，采用变铝柱高度来缓和这种温度梯度.研究了不同β 值对温度一致性的影响，当β=6 时单体间的温度一致性表现最好，相比于β=0，当β=6 时单体间的最高温度差降低了1.39 ℃.为使单体间的温度梯度达到最小，采用α=1 和β=6 的组合方式，经过观察，此组合方式下，模组的最大温差可降至3.72 ℃，相比于铝柱截面边长和高度为定值时单体间最高温度差降低了1.83 ℃.

文章的最后，研究了模型对于中低放电倍率下的温度分布.在0.5 C 和1 C 放电倍率下，单体间最大温差均在1 ℃以内；在2 C 放电倍率下，单体间最大温差为2.05 ℃，说明此电池冷却系统对调节电池温度一致性表现优异.