数形结合思想在高中数学解题中的有效渗透

伊斯马依力·吾吉艾麦提

摘要：在高中数学教学中，数学知识的学习与解题技巧受到越来越多人们的关注，为了构建高效课堂、促进教学实践活动的顺利开展，许多老师开始重新调整教学策略和教学方向，既坚持学生的主体地位，又十分关注教学策略和教学手段的稳定革新，在引导和鼓励学生的基础上丰富课堂教学内容和形式，保证学生在一个自由宽松的学习氛围下实现个人的良性成长和发展。

关键词：数形结合;高中数学教学;解题应用

引言

高中数学在很大程度上决定着高考成绩的高低，高中数学知识的学习对于很多同学来说存在一定的困难，因为需要对大量的数学概念进行记忆和应用，而数形结合的渗透，会帮助大家更好地掌握基础知识，为同学们高考成绩的提升提供保障。下面就来探讨数学学习中如何使用数形结合思想。

1数形结合思想方法

数与形是高中数学教学的重点和难点，老师需要了解不同的数量关系和空间图形分析要求之间的内在逻辑联系，结合学生的学习能力和学习背景，积极阐述数量关系与图形之间的转化关系。其中空间图形能够转变为数量关系，数量关系也可以直接转变为不同的空间图形，两者的联系和互动非常频繁。要想保证学生掌握高中数学学习的核心，老师必须要关注数与形之间的融合和转化，有效应用数形结合思想弥补学生在想象力和逻辑思维判断力上的不足，营造一个更加生动直观的学习氛围，让学生在自主学习的过程中，主动利用所学知识解决生活实际中的相关问题，将抽象困难的问题转化为简易的题目，通过不断的自主分析和独立思考提高学习积极性，产生源源不断的学习动力。

2数形结合思想方法在高中数学教学中的应用

2.1数形结合，简化习题结构

在高中数学中，“数”与“形”是学生在三年学习中的主要研究对象，只要找准二者之间在固定情境下的对应关系，就可以对二者进行任意转换。在高中数学解题过程中，数形结合这一数学思想的应用可以帮助学生简化实体条件。在很多情况下，原本很复杂、很抽象的题设条件用图像的形式表现出来，一下子就变得一目了然了，在这种前提条件下，以形助数可以帮助学生节省很大一部分的题目解析时间，提高学生的解题效率，而且，借助图像来辅助解题，有助于学生对数学概念的深层次理解。因此，在日常教学，教师就应该有意识地锻炼学生借助图形来分析题目的能力，让学生在短时间内抓住题干条件的重点，把题目中的隐含信息清晰地在图形上表现出来，借助图形去辅助简化遇到的问题。同时，教师在日常授课过程中，要着重注意对一些数学规律以及数学定理的证明，能用图形进行辅助证明时一定不要放过这次机会，让学生在一点一滴的积累中内化数形结合的思想。

2.2在方程问题中采用数形结合思想方法

方程问题是高中数学的核心模块之一。这一模块对学生的逻辑思维能力要求更高，老师可以着眼于数形结合思想方法，通过绘制数轴的形式，让学生对不同的方程有一个客观的认知。数形结合思想方法能够确定坐标轴之中抛物线的开口方向和焦点，学生可以在老师的引导下，在图形纸上画出不同的方程式，然后结合个人的社会生活实践经验和所学习的数学知识进行分析和迁移。这种教学策略能够加深学生的认知和理解，帮助学生梳理知识脉络和框架，从整体上提高学生的学习能力。

2.3利用数形结合解集合问题

在解答集合问题时，学生要完成答题需要一定的空间构思能力，也会有一定的难度。在集合问题中应用数形结合思想，可以让问题变得更加直观，提高学生解题效率，降低错误率。集合问题在运用数形结合的方法时，一般把圆视作一个集合，通过两圆相交、两圆相离的情况，可以直观地看出集合之间有没有公共的数集，对集合之间的关系可以有准确的把握。用画图的形式可以降低演算量，把计算简单化。在解不等式的取值范围问题时，可以利用画数轴图形的方式来解决问题，让问题变得简单。

2.4严谨清晰推理、强化解题能力

教师在数学解题中渗透数形结合思想，要注重对学生探究、批判、反思能力的综合培养，让学生在解题过程中能对数学语言进行细致入微的观察，通过周到、全面的自主构图进行严谨准确的分析思考，借助数形结合思想得出准确结论. 因此，为了进一步强化学生数形结合解题思想，教师可以组织学生运用常规解题思路，对比数形结合进行思考，让学生在对比、观察、归纳的分析中，能深刻感受到数形结合的价值优势，从而有效提高学生的解题意识和解题能力.

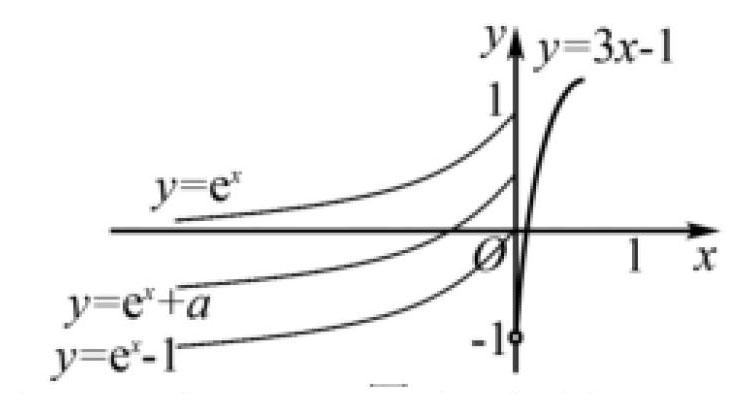
例如，已知函数（a∈R），若f（x）在 R 上有两个零点，求 a 的取值范圍. 在学生进行推理和构图的过程中，教师要遵循循序渐进的教学原则，让学生利用图形来揭示数学知识概念，通过感性到理性的认知，巧妙运用数形结合加深对数学知识的掌握理解. 如图所示：

当 x >0 时，f（x） =3x -1 有一个零点 x =1/3，因此，当x≤0，f（x） = e x + a =0 只有一实根。结合图形可知- 1≤a<0. 促使学生在解题过程中交叉灵活地融合抽象与形象思维，提高自身数学解题能力。

结语

综上所述，教师在数学课堂中渗透数形结合思想，要注重对学生发散性思维和直观思维的综合培养，引导学生在解题过程中灵活运用多向思维对问题进行分析、推理、联想，促使学生可以从整体角度，对数学问题结构本质进行识别判断，提高解决问题的效率和灵活性。同时，教师要为学生提供充足的思考空间，让学生在自主探索、讨论交流解题过程中，大跨度地迁移思路和方法，通过数与形的巧妙结合，创造性地解决问题。

参考文献

[1]王小峰.探析高中数学教学过程中常用的思想方法[J].数学学习与研究，2018，（9）：41.

[2]苏心怡.数形结合思想在高中数学解题中的应用浅析[J].考试周刊，2019（15）：104.

[3]李晓明.高中数学教学与解题中数形结合思想方法的应用分析[J].中国新通信，2018，20（07）：209.