一道选择题引发的思考

方婷

清明时节雨纷纷。在这个不一样的节日里，沉淀自己的心情，反思上次数学练习的错误。

3月底进行了一次数学练习，是根据高考的难度要求，与《2013浙江理、文样卷10》的类似题型：

如右图，函数y=f（x）的图像为折线OAB，设g（x）=f[f（x）]，则满足方程g（x）=x的根的个数为（）

A.2个                B.4个                C.6个                 D.8个

命题背景：函数的迭代。用图像给出一个具体的分段函数，让学生进行迭代得到新的函数，画出图像，从而数出与函数y=x的图像的交点个数。主要考查学生由图像得函数解析式的能力，对函数的代入运算及严密的数学逻辑分析能力，充分运用了数形结合的思想。

可是不要解析式，如何单靠图像解决？

因为y=f（x），所以g（x）=f[f（x）]=f（y），若g（x）=x，则f（y）=x，所以有y=f（x），x=f（y），所以有x=y，则函数y=f（x）与函数y=x图像的交点个数为2，与正确答案相悖。

其实对照标准答案很容易发现，一个是y=g（x）与y=x相交，一个是y=f（x）与y=x相交，显然后一种是错的。那么，后一种方法的错处在哪里？其实，y=f（x），f（y）= x，并不是简单的得到x=y，而是一个变换，一个迭代的变换。第一个式子的图像上的点可以用（x，y）表示，而第二个式子图像上的点则可用（y，x）表示，即g（x）=f[f（x）]=f（y）=x的根的个数，实质是函数y=f（x）的图像与它关于y=x的对称的图像的交点个数。如图所示。

这个方法很是快速，特别是对此题要进行分段函数的迭代。那是否具有通用性呢？追溯原因，在于g（x）=x，若此题变为g（x）=2x，还可否如此简单？答案是：方法超过考试大纲，但是也可解。因为y=f（x），所以g（x）=f[f（x）]=f（y），若g（x）=2x，则f（y）=2x，即x=f（y），若y为横坐标，x为纵坐标，则图像横坐标不变纵坐标变为原来的。要在一个坐标系中表示，则如图示：

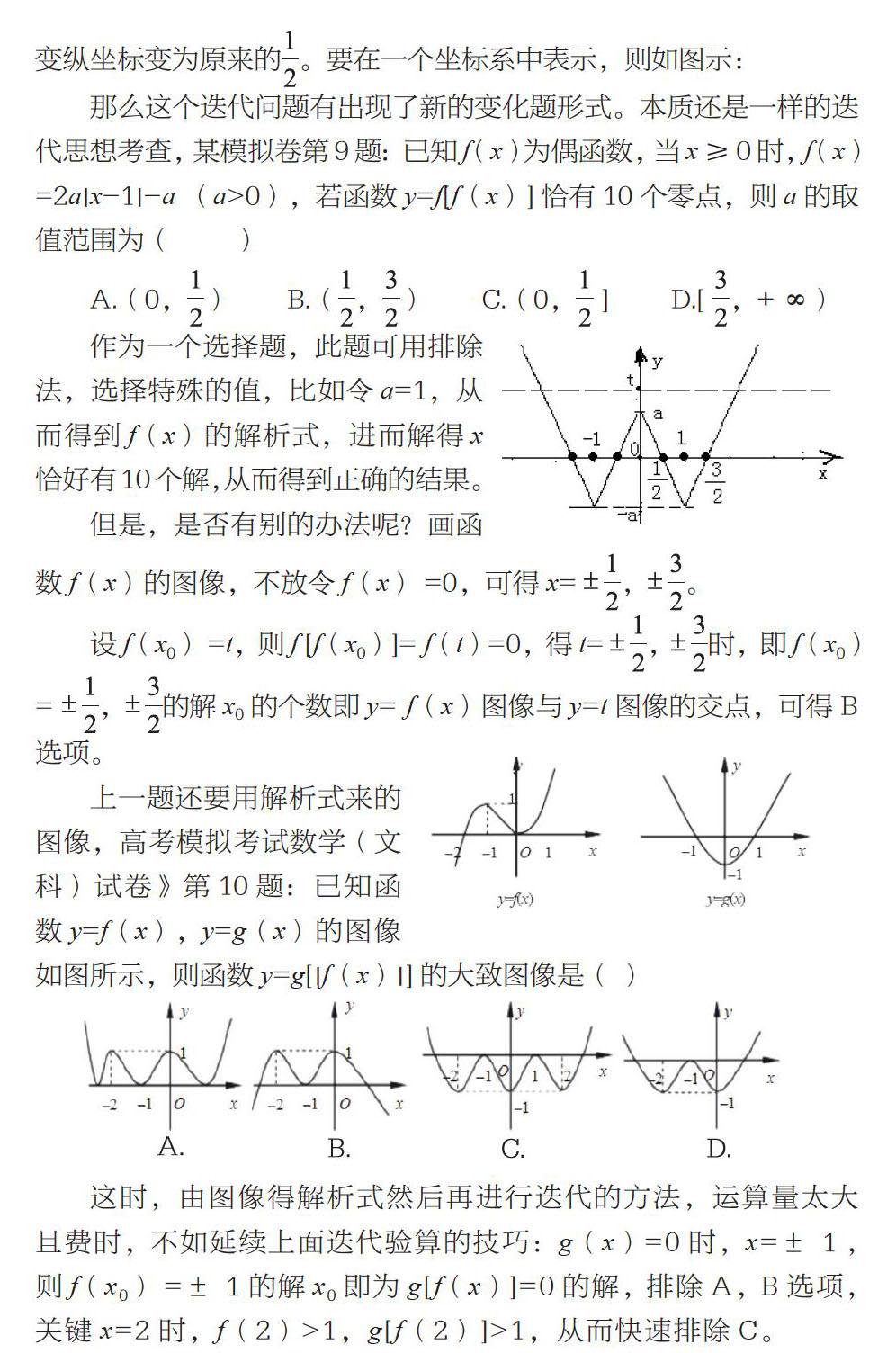
那么这个迭代问题有出现了新的变化题形式。本质还是一样的迭代思想考查，某模拟卷第9题：已知f（x）为偶函数，当x≥0时，f（x）=2a|x-1|-a （a>0），若函数y=f[f（x）]恰有10个零点，则a的取值范围为（ ）

A.（0，）B.（，）C.（0，] D.[，+∞）

作为一个选择题，此题可用排除法，选择特殊的值，比如令a=1，从而得到f（x）的解析式，进而解得x恰好有10个解，从而得到正确的结果。

但是，是否有别的办法呢？画函数f（x）的图像，不放令f（x） =0，可得x=，。

設f（x0） =t，则f [f（x0）]= f（t）=0，得t=，时，即f（x0）= ，的解x0的个数即y= f（x）图像与y=t图像的交点，可得B选项。

上一题还要用解析式来的图像，高考模拟考试数学（文科）试卷》第10题：已知函数y=f（x），y=g（x）的图像如图所示，则函数y=g[|f（x）|]的大致图像是（ ）

这时，由图像得解析式然后再进行迭代的方法，运算量太大且费时，不如延续上面迭代验算的技巧：g（x）=0时，x=±1，则f（x0） =±1的解x0即为g[f（x）]=0的解，排除A，B选项，关键x=2时，f（2）>1，g[f（2）]>1，从而快速排除C。

其实，分段函数迭代问题无数变式不胜枚举，但是函数问题的本质永远是数形结合的思想，利用函数的性质可知图像，也可由函数图像得性质。华罗庚曾经说过：“数缺形时少直观，形少数时难入微，数形结合百般好，隔离分家万事休。”在这类题型中真是最体现了此思想方法的快捷简便。

数学教学应引导学生注重数学知识基础的同时，也要真正理解数学的思维和思想方法，在能力的培养过程中感悟数学。在课堂上，教师应该以概念为基础，以思想方法为主线，以知识为载体进行教学，不断反思、总结，才能不断提升。