基于Davidenkov模型的北部湾海岸混合土动力特性试验研究

刘 雄，张小波，王杰光

(1.中国电建集团中南勘测设计研究院有限公司，湖南 长沙 410014；2.湖南省体育职业学院，湖南 长沙 410014；3.桂林理工大学，广西 桂林 541004)

0 前 言

近年来，地震海啸等自然灾害频发，引发了对于各类土体的灾害机理研究的进一步深入。而在工程实际中，各类土体对地震的表现形式各不相同，在密度、强度、变形特性等宏观参数相似情况下，非均质砂土中由地震引起的孔压增长明显大于均质砂土。但是，传统的土动力学理论尚无法有效地描述这种差异性，这使得传统的动态分析方法在分析饱和非均质土的振动破坏问题时得出偏于危险的结论[1-2]。另外，目前岩土工程理论和实践完全没有考虑水化学和动态荷载联合作用对结构物地基和基础的长期稳定性影响，这将给结构物安全设计带来重大隐患。

因此，对于非均质土体(即“混合土”)的动力特性的研究非常有必要。反映土体动力特性的参数主要有土层的剪切波速vs，动剪模量比G/Gmax以及阻尼比λ[3]。本文选取北部湾地区北海-合浦一带混合土作为试验对象，通过共振柱试验对混合土在小应变条件下动剪模量比G/Gmax以及阻尼比λ进行测试和分析，在试验的基础上对混合土的动力特性进行研究。

1 混合土动力特性计算理论

关于土的动力特性研究，通常有两种：一种是直接关系到土的抗震稳定性的参数，比如动强度、土体液化特性、震陷特性等；另一种是地震波在传播过程中，土体作为介质时表现出来的性质，比如动剪切模量、阻尼比以及振动条件下的体积模量和泊松比等。本文主要考虑的是混合土的动剪切模量和阻尼比在控制不同条件时的变化趋势，并基于Davidenkov模型[4]对土体动力参数变化曲线进行拟合，总结得出混合土在不同性质不同条件时的动力特性。

1.1 基本理论与公式

关于结构模型中动剪切模量和阻尼比与动应变的关系，最早是1926年Masing建立的在等幅循环荷载作用下，金属材料的一维态的动应力-应变关系。该模型阐述了动剪切模量和阻尼比与动应变结构模型建立的三项基本规则，也就是“Masing法则”，即：动应力-应变关系的中心曲线为双曲线假定，在初始加载阶段应力应变关系遵循中心曲线的发展趋势，动剪切模量G与最大剪切模量Gmax在初始反向卸载阶段相等。

但是釆用双曲线作为中心曲线的动本构关系模型和土体实际动应力-应变关系本身就存在相当大的不确定因素，在试验结果拟合时，可选取的参数量较少，因此土体动剪切模量比G/Gmax～动剪应变γ曲线的拟合结果与原位测量间误差较大。针对这点，Hardin[5]等人在1972年提出了动剪切模量比G/Gmax和剪应变γ的关系式：

此后，在Hardin的基础上Martin等人利用Davidenkov模型进行改进，提出了采用三参数A、B和γ0对G/Gmax～γ曲线进行拟合的方法，该方法拟合的各类土体的G/Gmax～γ曲线的试验结果较为理想和准确，符合实际应用标准。

(1)

式中，A、B和γ0皆为拟合参数，这里的γ0不代表一个具有明确物理意义的剪应变幅。它的完整应力应变公式为：

τ(γ)=G·γ=G·γ·[1-H(γ)]

(2)

本文试验采用GZZ-70型共振柱进行扭转振动试验，试验中所得试验结果由内置程序直接计算出动剪切模量，阻尼比和动剪应变，其具体计算公式有以下几个：

(1)计算无弹簧支承扭转共振时的动剪切模量

(3)

式中，G为动剪切模量，kPa；Fn为试验时实测的共振频率，Hz；Hc为试样固结后的高度，cm；ρ0为土试样的密度，g/cm3；βs为无量纲频率因素(βstgβs=I/It)程序中由解频率方程给出；It为试样顶端附加物质量惯性矩，由标定确定。

(2)计算土的阻尼比

(4)

式中，λ为阻尼比；N为计算所取得的振动次数；A1为停止激振后第1周振动的振幅，mm；AN+1为停止激振后第N+1周振动的振幅，mm。

(3)计算试样的应变[6]

(5)

式中，γ为动剪应变，%；A为安装加速度计处的动位移，(A=U/βω2)，cm；U为加速度计经放大后的电压值；β为标定系数，mV/981 cm/s2；ω为共振圆频率，(2πfn)rad/s；d1为加速度计到试样轴线的距离，cm；dc为试样固结后的直径，cm；hc为试样固结后的高度，cm。

2 试验原材料

2.1 试验原材料及基本物理性质

本文试验所取用的土样均为北部湾地区北海-合浦一带的近海回填混合土，取土采用机械为百米型钻机，深度为6～8 m。通过烘干法测得的混合土的天然含水率为18.35%，天然干密度为1.58 g/cm3，比重为2.70，天然孔隙比为0.71，通过筛分法，锥式液限测定以及其他物性试验，得到该土样的基本物理性质，如表1所示。

表1 混合土土样的基本物理性质

2.2 试验设备

本文共振实验采用的是江苏永昌科教仪器制造有限公司生产的GZZ-70型共振柱实验仪(如图1所示)。GZZ-70型共振柱试验仪是由计算机控制的土动力试验仪器，可在试样未破损的小应变范围内(10-6～10-3)研究土的动力性质，主要用自由振动方法确定土的动剪切模量G和阻尼比λ值，也可用共振法确定土的动弹性模量E、动剪切模量G和阻尼比λ值。

GZZ-70型共振柱试验仪在进行水平扭转方向振动试验时，采用自由振动法试验直接给出动剪切模量、阻尼比和相应的剪应变，在轴向振动试验时，用轴向共振法测算出动弹性模量、阻尼比和轴向应变，同时由于电脑新软件的应用，替代了原来SL237-033-1999规范中关于共振柱试验规程中信号发生器，频率计和示波器等模拟表的手动操作要点，采用电脑自动完成土的动弹性模量的测定。

图1 GZZ-70型共振柱实验仪

3 试验方案与步骤

3.1 试验方案

本文以北部湾地区北海-合浦一带的近海回填混合土为研究对象，采用 GZZ-70型共振柱试验仪对原位和重塑回填混合土体进行不同干密度，含水率和不同围压下的共振柱试验，不等向固结的共振柱试验试样的个数为3×3×3=27个，同时对原状土进行3个不同围压下的共振柱试验。重塑土试验的具体条件控制如表2所示。

表2 共振柱试样的试验参数

3.2 试验步骤

(1)试样制备：原状土样采用切削法直接进行制取。重塑土样通过控制不同含水率，利用制样器采用分层击实法制得，相关操作与三轴试验规程相同。

(2)设备检查与预热：打开电源，将电荷放大器、功率放大器预热30 min，检查激振系统、量测系统和气源控制柜的工作状况，查看各管口及压力室是否漏水或漏气。

(3)试样装载：将试样装入套有乳胶膜的承膜筒中，刷干净下加压头的杂物，并在其刀片上铺上湿滤纸，将试样与承膜筒对准刀片放置，将承膜筒下滑，使底部多余乳胶膜翻下套于下压头，然后撤去承膜筒，用对开筒护于试样两侧，用橡皮筋箍筋，并将顶部多出的乳胶膜反套于对开筒上，保持对开筒直立不变形，用试样压块轻压对开筒，使试样底部完全插入刀片，然后上压头对准试样顶部，用掌力压水平扭转板，使上压头的刀片插入试样，再将上部乳胶膜翻上套入上压头，接着撤去对开筒，平整上下压头的乳胶膜，并用橡皮筋箍紧，保证密封性。

(4)安装压力室罩子，两边抬起机罩紧固机罩顶部与试验激振室底部的四个螺钉，保证整个压力室的密封。

(5)试样固结：量测系统调零，打开进水阀，注水直到漫过试样1 cm处，关闭压力室放气阀门，打开控制柜气源阀门，顺时针转动调压阀，调节至相应固结围压σ3，打开压力室底座排水阀门，通入气体进行固结，参照三轴试验规程，当固结时间达到真三轴固结试验所用时间时即视为固结完成。

(6)激振：在预热各仪器后，功率放大器在不开增益开关时，可以从示波器上观察到由于地面微动产生的干扰信号，以及在仪器附近说话的声波激发的小信号，说明量测系统已经工作，干扰信号视环境而定，一般在5～10 MV之间。然后将功率放大器增益灵敏度调小30%左右，启动激振加载，然后进行扫频输出，此时监视屏幕波形大小，在改变频率时振幅随着频率接近共振点而加大，通过共振点后波幅减小直至设定频率，扫频停止，显示共振曲线，框表中自动计算出模量、应变和阻尼比。此时完成一个应变量级试验，加大功率放大器增益灵敏度，进行下一级试验，自由振动法整个试验过程一般分为十二步激励过程，扭力从小到大，直至剪应变达1×10-3时停止，保存试验记录数据。

(7)试验结束：打开压力室放气阀门，卸载围压σ3，同时打开排水阀门，待水和气排净后拆下压力罩、拆下试样，依次关闭气泵、量测系统和功率放大器电源，整理实验数据。

4 试验结果分析

通过查阅大量资料并结合工程实际，发现对混合土体动力特性影响较大的因素有很多，其中包括固结围压、干密度、含水率、细粒含量以及激振频率等。本文通过控制不同条件下的混合土的共振柱试验，得出各条件下的动剪切模量比G/Gmax和剪应变γ的拟合曲线，并得出基于Davidenkov模型的拟合参数A、B和γ0。

4.1 原状土与重塑土的动剪切模量比和剪应变曲线

在探讨重塑混合土动力特性的同时，本文对原状土与重塑土的动力参数关系进行了研究。在通过对天然含水率ω为18%，天然干密度ρd为1.55 g/cm3的原状土样及相同物理性质的重塑混合土样，在固结围压为100 kPa的条件下进行共振柱试验并对结果进行拟合(见图2和图3)。从图2可以看出，在控制试验条件相同的情况下，混合土原状样与重塑样的动剪切模量比G/Gmax和剪应变γ曲线表现形式基本上是一致的，随着剪应变的增加，土体的动剪切模量比都逐渐减小。在剪应变在1E-7～1E-4较小范围内，动剪切模量比的衰减速率相对较慢，且原状混合土较重塑土变化更小。但随着剪应变的增大，曲线逐渐变陡，其衰减速率也明显增大，而当剪应变增大到1E-3以上时，曲线又重新趋于平缓，此时原状土和重塑土的动剪切模量比衰减速度也几乎相同。整体上来看，土样的动剪模量比的衰减规律符合土体的非线性和滞后性的一般规律。从图3可以看出，土样的阻尼比和剪应变曲线表现形式与动剪切模量比和剪切应变曲线的表现形式刚好相反，随着剪应变的增加，土体的阻尼比逐渐增大，在剪应变在1E-7～1E-4较小范围内，阻尼比的衰减速率相对较慢，在相同应变量时，原状混合土的阻尼比较之重塑土更小。

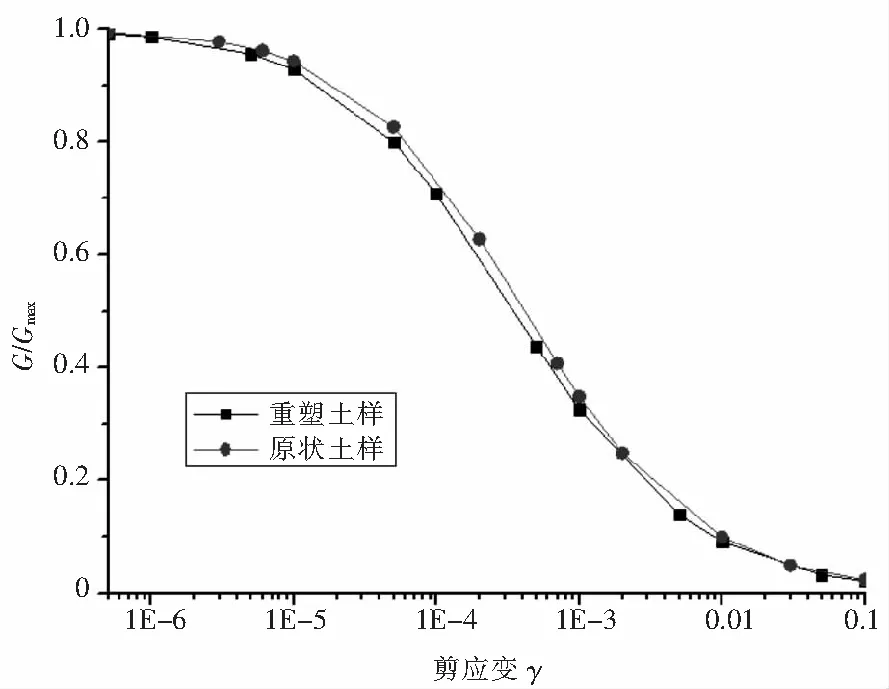
图2 原状土样与重塑土样G/Gmax～γ曲线(ρd=1.55 g/cm3，ω=18%)

图3 原状土样与重塑土样λ～γ曲线(ρd=1.55 g/cm3，ω=18%)

4.2 固结围压的影响

试验控制重塑土样的其他条件和基本物性，即干密度、含水率、激振频率和黏粒含量，在不同的固结围压下进行扭转激振，可以得到重塑混合土在固结围压为50 kPa，100 kPa和150 kPa下的动力特性。

在通过对干密度ρd为1.55 g/cm3，含水率ω为18%的重塑混合土样在固结围压为50 kPa，100 kPa和150 kPa的条件下进行共振柱试验，对所得试验结果进行曲线拟合，得到G/Gmax～γ曲线(见图4)和G～γ曲线(见图5)。从图4可以看出，在围压不同的条件下，重塑混合土的动剪模量比与剪应变的关系变化基本上是一致的，剪应变在1E-7～1E-4的较小范围内，动剪切模量比的衰减速率都比较慢，且围压大的土样衰减速度相对更小，但总体相差不大，以Davidenkov模型公式拟合可得到各参数值：当围压为50 kPa时，A=1.037 8，B=0.736 6，γ0=0.000 231 5；当围压为100 kPa时，A=1.133 4，B=0.675 3，γ0=0.000 270 9；当围压为150 kPa时，A=1.202 5，B=0.596 6，γ0=0.000 291 3。从图5可以看出，在围压不同的条件下，重塑混合土样所表现出的最大动剪模量各不相同，在相同应变下，围压越大，动剪模量也越大。这是因为试样的围压越大，土颗粒更加密集，表现出的孔隙比也越小，颗粒间触点增加，从而使剪切波在土中传播速度加快，增大土体动模量。同时，随着应变增量变大，围压和孔隙比的影响也逐渐减弱。

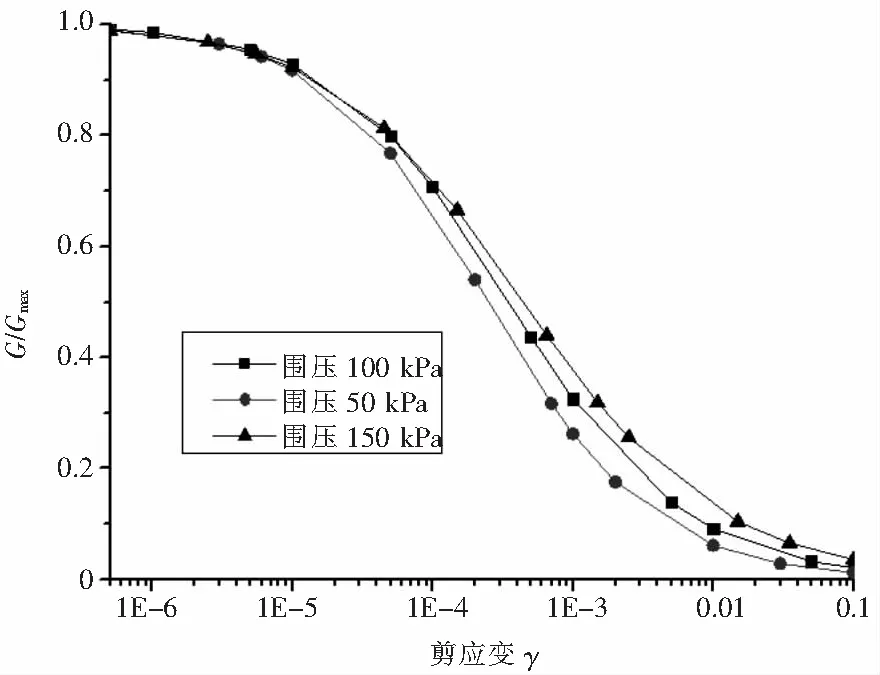
图4 不同围压下的G/Gmax～γ曲线(ρd=1.55 g/cm3，ω=18%)

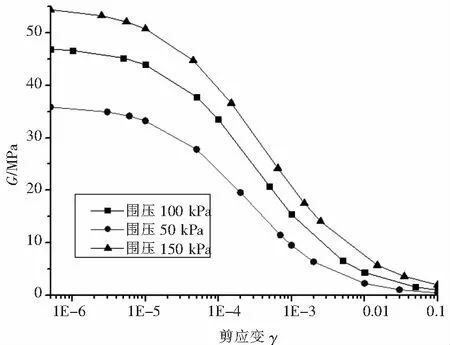
图5 不同围压下的G～γ曲线(ρd=1.55 g/cm3，ω=18%)

4.3 干密度的影响

与上述试验相同，同样通过控制重塑土样的其他条件和基本物性，即固结围压、含水率、激振频率和黏粒含量，对不同干密度的土样进行扭转激振，可以得到重塑混合土在1.3 g/cm3，1.55 g/cm3和1.7 g/cm3下的动力特性。

在通过对含水率ω为18%，干密度分别为1.3 g/cm3，1.55 g/cm3和1.7 g/cm3的重塑混合土样在固结围压为100kPa的条件下进行共振柱试验，对所得试验结果进行曲线拟合，得到G/Gmax～γ曲线(见图6)和G～γ曲线(见图7)。从图6可以看出，重塑混合土的动剪模量比随剪应变的增大同样呈递减的趋势，干密度较大的土样的动剪切模量比的衰减速率比干密度小的土样整体要慢，在剪应变在1E-7～1E-4的应变范围内范围内，动剪切模量比变量较小，1E-4～1E-3的应变阶段，则明显加快，动剪模量比变化较大，当应变达到1E-3以上时，又变得平缓时。以公式(1)拟合可得各参数值：当ρd=1.3 g/cm3时，A=1.060 8，B=0.742 3，γ0=0.000 258 7；当ρd=1.55 g/cm3时，A=1.133 4，B=0.675 3，γ0=0.000 270 9；当ρd=1.7 g/cm3时，A=1.253 6，B=0.623 3，γ0=0.000 282 1。从图7可以看出，不同干密度的土样随着剪应变的增加，动剪模量不断减小；土样干密度不同，重塑混合土样所表现出的最大动剪模量也不相同；在相同应变条件下，干密度越大，动剪模量也越大。

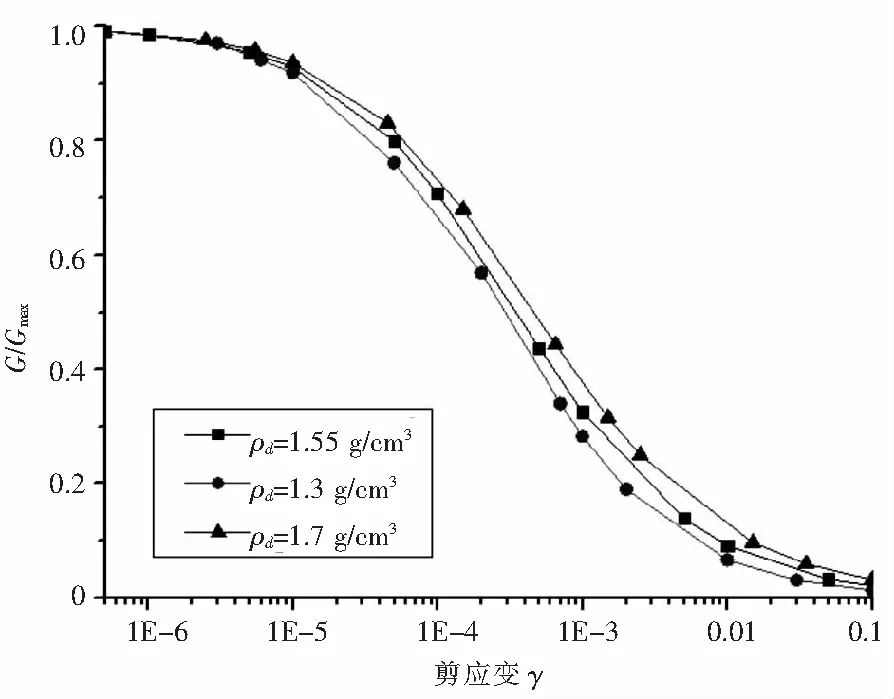
图6 不同干密度下的G/Gmax～γ曲线

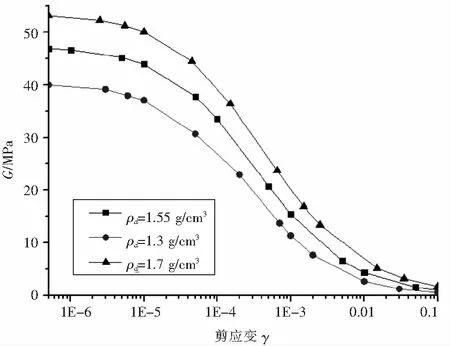
图7 不同干密度下的G～γ曲线

4.4 含水率的影响

通过阅读文献和查阅岩土研究成果，对于土体动剪模量比与孔隙比和黏粒含量的变化关系研究比较多，而在关于含水率对土体动剪模量比的影响方面的研究相对较少，大多数研究成果或者理论模型都是建立在土体饱和的前提上的，本文针对于此，对不同含水率的土样进行了扭转激振的共振柱试验，期望探讨得到重塑混合土在含水率为15%、18%和21%情况下的动力特性。

同样的，在通过对干密度为1.55 g/cm3，含水率为15%、18%和21%的重塑混合土样在固结围压为100 kPa的条件下进行共振柱试验，对所得试验结果进行曲线拟合，即G/Gmax～γ曲线(见图8)和G～γ曲线(见图9)。从图8可以看出，不同含水率下的动剪模量比与剪应变的变化关系与之前的试验结果相差无二，随着剪应变的增加，试样的动剪切模量比的取值逐渐减小，在剪应变较小时，动剪切模量比的衰减速率较慢，随着剪应变的增大，曲线逐渐变陡，其衰减速率明显增大，当剪应变增大到1E-3以上时，衰减现象不太明显。以公式(1)拟合可得各参数值：当ω=15%时，A=1.153 6，B=0.633 5，γ0=0.000 280 3；ω=18%时，A=1.133 4，B=0.675 3，γ0=0.000 270 9；ω=21%时，A=1.121 6，B=0.711 2，γ0=0.000 262 3。从图9可以看出，不同含水率下的动剪模量相差在10%以内，在该范围内的含水率大小对重塑混合土试样的动剪模量的影响并不大，较之其他影响因素要小很多，在实际应用中，涉及土体动剪模量计算的，可以优先考虑其他影响因素。

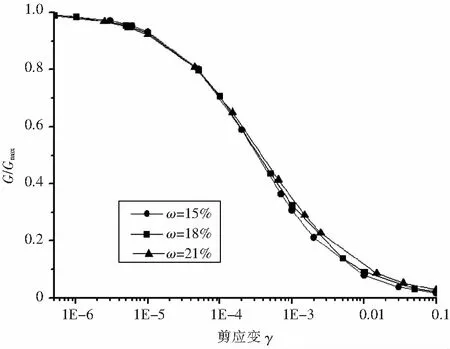
图8 不同含水率下的G/Gmax～γ曲线

图9 不同含水率下的G～γ曲线

5 结 语

通过对试验结果分析研究，可以得到：

(1)在试验条件相同的情况下，混合土原状样与重塑样的动剪切模量比G/Gmax和剪应变γ曲线表现形式基本上是一致的，随着剪应变的增加，土体的动剪切模量比都逐渐减小。整体上来看，土样动剪模量比的衰减规律符合土体非线性和滞后性的一般规律。而土样的阻尼比和剪应变曲线表现形式与动剪切模量比和剪切应变曲线的表现形式刚好相反，随着剪应变的增加，土体的阻尼比逐渐增大，且在相同应变量条件时，原状混合土的阻尼比较之重塑土更小。

(2)在围压不同的条件下，重塑混合土的动剪模量比与剪应变的关系变化基本上是一致的，剪应变在1E-7～1E-4的范围内，动剪切模量比的衰减速率都比较慢，且围压大的土样衰减速度相对更小，但总体相差不大，以公式(1)拟合可得各参数值：当围压为50 kPa时，A=1.037 8，B=0.736 6，γ0=0.000 231 5；当围压为100 kPa时，A=1.133 4，B=0.675 3，γ0=0.000 270 9；当围压为150 kPa时，A=1.202 5，B=0.596 6，γ0=0.000 291 3。

(3)重塑混合土的动剪模量比随剪应变的增大同样为递减的趋势，干密度较大的土样的动剪切模量比的衰减速率比干密度小的土样整体慢。以公式(5)拟合可得各参数值：当ρd=1.3 g/cm3时，A=1.060 8，B=0.742 3，γ0=0.000 258 7；当ρd=1.55 g/cm3时，A=1.133 4，B=0.675 3，γ0=0.000 270 9；当ρd=1.7 g/cm3时，A=1.253 6，B=0.623 3，γ0=0.000 282 1。

(4)不同含水率下的动剪模量比与剪应变的变化关系与之前的试验结果相差无二，以公式(5)拟合可得各参数值：当ω=15%时，A=1.153 6，B=0.633 5，γ0=0.000 280 3；当ω=18%时，A=1.133 4，B=0.675 3，γ0=0.000 270 9；当ω=21%时，A=1.121 6，B=0.711 2，γ0=0.000 262 3。不同含水率下的动剪模量相差在10%以内，在该范围内的含水率大小对重塑混合土试样的动剪模量的影响并不大，较之其他影响因素影响要小很多。在实际应用中，若涉及土体动剪模量计算，可以优先考虑其他影响因素。