基于二次破坏模式下浅埋隧道围岩压力上限分析

2020-06-29曹世江

水电站设计 2020年2期

刘毅，程宏，曹世江

(1.中国电建集团贵阳勘测设计研究院有限公司，贵州贵阳 550081；2.中国水利水电第十四工程局有限公司，云南昆明 650501)

0 前言

隧道浅埋施工中，围岩压力、围岩破坏模式是隧道施工关键技术问题，围岩是隧道周围在隧道开挖后应力重分布的土体(岩体)，隧道围岩压力即隧道开挖后直接作用在支护结构上的压力。目前，计算围岩压力较多采用的是公路隧道设计规范[1-2]推荐的方法、文献[3]提及的太沙基计算方法，这都是基于极限平衡理论求解出的围岩压力。因此，近几年以来，国外内大量学者采用极限分析理论研究浅埋隧道围岩压力：极限分析分为极限上限分析、极限下限分析[4-6]，对于分析目标分别满足破坏速度场和破坏应力场。采用极限分析理论研究浅埋隧道围岩压力，即对计算围岩压力引入极限分析理论，其中应用较多的是极限分析上限理论，如：国外学者Atkinson[7]对砂性土浅埋隧道稳定性问题引入极限分析上下限理论进行研究，并利用模型试验方法验证结果正确性；Leca[8]等利用极限分析上下定理论研究浅埋隧道破坏模式问题，并根该模式准确计算出浅埋隧道掌子面稳定性的极限支护压力；Soubra[9-10]等在Leca[8]研究基础上，采用极限分析上限理论研究浅埋隧道三维破坏模式，提出更加准确的围岩压力计算解；国内学者杨小礼[11-12]、赵炼恒[13]、孙雁军[14-15]、张佳华[16]等采用极限分析上限理论研究浅埋隧道围岩压力的准确计算。杨小礼基于极限分析上限理论，引入浅埋隧道竖向刚体破坏模式及非线性破坏准确，研究不同围岩参数对隧道破坏模式及围岩压力的影响分析；赵炼恒基于非关联流动法则与分析上限理论，推到非关联流动法则下浅埋隧道围岩压力计算公式；孙雁军构造浅埋隧道两种不同的破坏模式，推导出相应围岩压力计算公式，并研究围岩参数与隧道围岩压力之间的演变规律。张佳华基于极限分析上限理论，引入至浅埋偏压隧道、非偏压隧道两种情况，讨论地震作用下浅埋隧道的围岩压力。

然而，已有研究建立在考虑剪胀角影响基础上，但速度间断线与构造速度场之间剪胀关系未完全考虑，并且构造破坏多为一次直接破坏。

1 极限上限分析与破坏模式

1.1 上限分析原理

上限分析实质是极限分析的推广，其在岩土工程中得到了较广泛的应用，尤其在极限分析计算过程中，摒弃了岩土应力-应变之间复杂的关系，代之以理想的流动法则方式考虑土体的本构关系。上限分析理论的理论基础严谨、计算方便，结果求解利用优化算法求得，结果更加真实可靠。根据Chen的观点，上限分析可表述为：构造一个运动许可的速度场，速度场满足边界条件和速度相容条件，根据虚功原理求出的解一定大于或等于真实解。

(1)

1.2 破坏模式

目前，浅埋隧道的破坏模式已经有较多学者进行了研究，多集中在泰沙基破坏模式和公路隧道破坏模式。两种破坏模式均考虑浅埋隧道的整体破坏，其中泰沙基破坏模式考虑两种不同的速度破坏模式，公路隧道破坏考虑三种不同的速度破坏模式，速度之间构成速度矢量场闭合关系。在浅埋隧道破坏模式中，隧道的开挖将波及地表形成“自然拱”现象；形成自然拱后，自然拱两侧的围岩不能持续平衡，继续发生岩土的坍塌，从而形成在隧道拱顶一定范围的坍塌现象。而现有的文献分析[11-16]研究未考虑隧道拱顶塌方的破坏先后关系，仅采用最终阶段考虑隧道发生的破坏模式进行分析。文献[11-16]应用的分析方法皆为该种方法，若对破坏模式进行改进，便能较准确地求出围岩压力的极限分析计算解。因此，本文基于泰沙基破坏模式、公路隧道破坏模式及其他一系列学者研究，根据工程实际经验提出一种考虑浅埋隧道拱顶塌方破坏先后关系的破坏模式，如图1中(a)所示：H表示隧道拱顶与水平地表面之间的垂直距离；h为隧道洞直径；破坏模式包含破坏面BC、破坏面AB、破坏面BE，浅埋隧道掘进时，两侧边墙破坏引起拱顶坍塌形成“自然拱”现象，拱顶两侧由于受力失稳，进而造成两侧土体进一步破坏，最终整体坍塌。

研究以非偏压情况下隧道破坏模式进行探讨，图1(b)表示该破坏模式下各破坏土体之间速度场的矢量构成关系：V0为上覆土体速度；V1、V01、V2、V20分别为间断线的速度。图中只列出左侧部分，右侧部分对称左侧；速度与间断线之间夹角为内摩擦角φ，破裂角为α、β、δ。

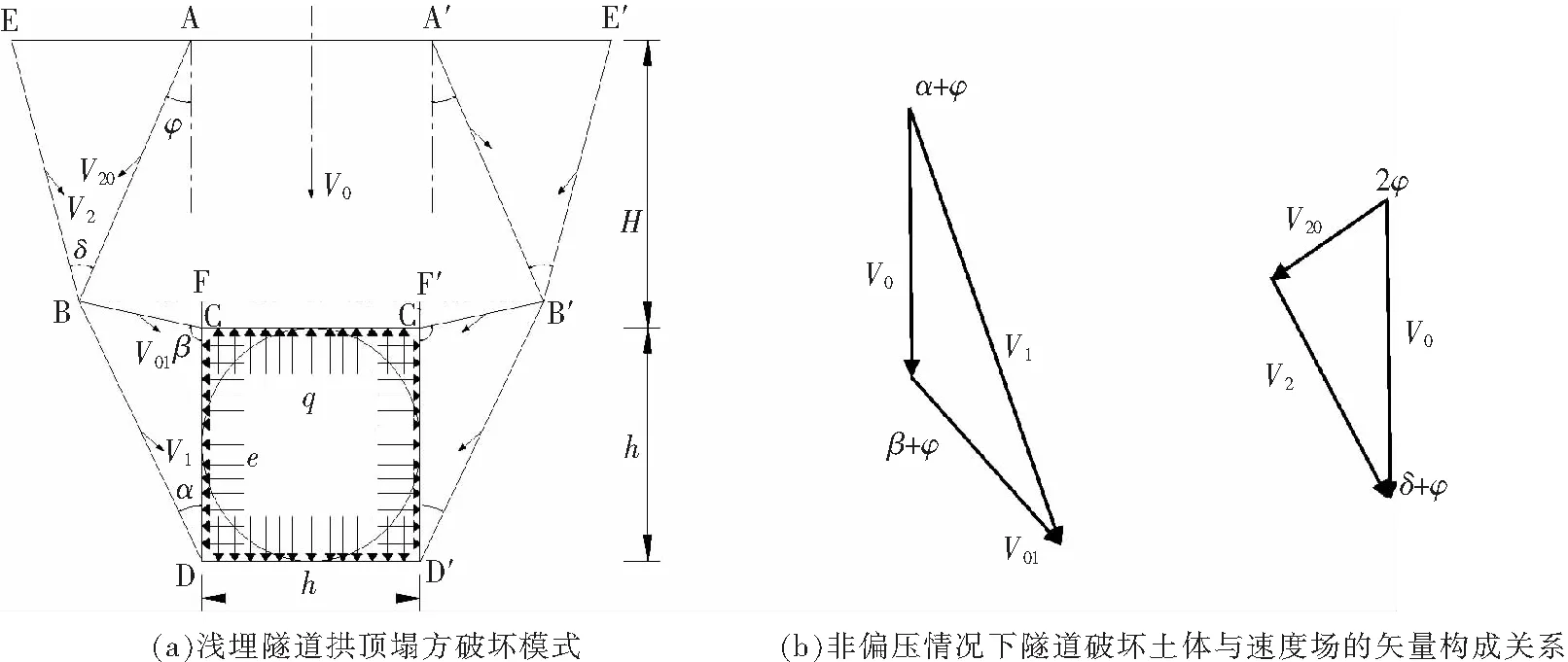
图1 浅埋隧道破坏模式及对应速度场

2 能量分析

2.1 计算假定

采用极限分析上限定理进行浅埋隧道破坏分析时，假定如下：

(1)简化为二维破坏模式分析；

(2)围岩为理想塑性材料，服从相关联流动法则，并忽视破坏对参数影响；

(3)圆形隧道等效为矩形计算，并且侧压力系数取K；

(4)破坏间断线能量满足叠加原理。

2.2 隧道围岩压力极限分析

2.2.1 外力所做功功率

速度满足闭合条件，如图1所示，隧道破坏模式各速度之间关系如下：

(2)

(3)

隧道破坏模式下各间断线长度可以h、α、β等参数表示。

浅埋隧道外力做功分两部分，一是重力做功，二是支护反力做功。重力做功功率P=γSV，其中γ为土体重度。

(4)

(5)

(6)

重力做功考虑到左右部分对称，因此：

W1=WABCC′B′E′+2WBCD+2WEAB

(7)

式中，WABCC′B′E′=γSABCC′B′E′V0；WBCD=γSBCDV1cos(α+φ)；WEAB=γSEABV2cosδ。

支护反力做功，分拱顶、左右边墙两者做功之和，即：

W2=-qhV0-2×ehV1sin(α+φ)

(8)

2.2.2 间断线能量耗散率

能量耗散率为间断线能量和，即：

Wint=2c×lEB×V2cosφ+2c×lAB×V20cosφ+2c×lBC×V01cosφ+2c×lBD×V1cosφ

(9)

2.3 围岩压力

根据虚功原理得浅埋隧道竖向支护力计算公式：

W1+W2=Wint

(10)

则：

(11)

式中，f1，f2，f3，f4，f5是与H，h，α，β，δ等一系列有关的函数。

利用MATLAB编程计算软件[17]，采用优化算法，问题等效于求满足边界条件下求目标函数的最优解问题，其中约束条件为：

编写相应的计算程序，利用SQP优化算法对问题模型进行分析(见图2)。

3 隧道围岩压力及破坏分析

为分析研究浅埋隧道支护力及破坏模式，进行上限极限分析，引用类似文献，其中参数假定为：浅埋隧道埋深H=20 m，跨度h=10 m，围岩重度γ=20 kN/m3，内摩擦角φ=18°，黏聚力c=10.0 kPa。

3.1 对比分析

为验证计算结果正确性，将本次上限分析解与经典计算方法-泰沙基极限平衡解进行比较(如表1所示)。计算结果表明，当K取值在1.3～1.5范围时，计算结果与泰沙基计算结果比较接近。

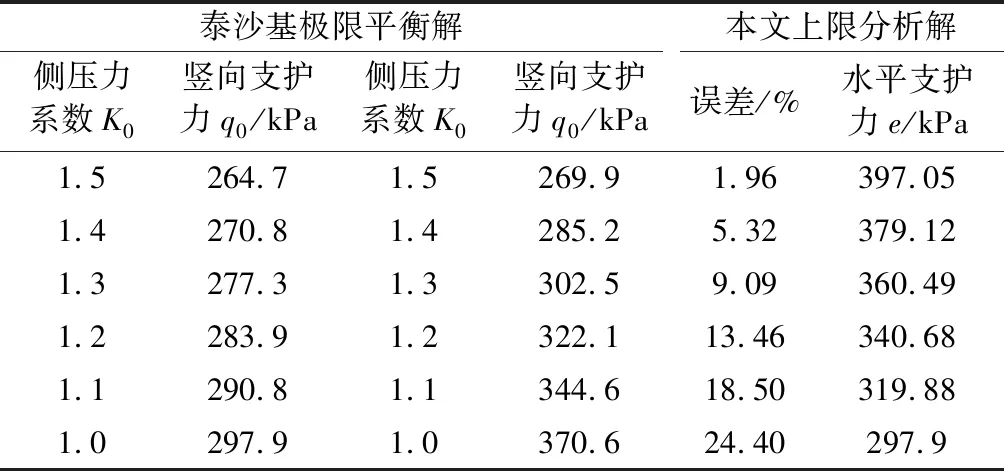
表1 计算结果对比经典计算结果

3.2 侧压力系数K分析

从目标函数可知，侧压力系数K影响目标函数优化计算值，讨论侧压力系数对支护反力的变化影响关系。研究K在1.0～1.5变化时，支护反力的变化情况。从图2可知，对于浅埋隧道支护反力，竖向支护力q随侧压力系数K增大非线性减小，水平支护力e随侧压力系数K增大非线性增大，说明对于浅埋隧道，隧道围岩支护压力与侧压力系数K有关。侧压力系数K对破坏模式如图3所示，由图3看出，随着侧压力系数增大，破裂角α呈减小趋势；β始终保持不变角度，说明侧压力系数不影响破裂角β；破裂角δ呈减小趋势。综上所述，破裂角α、δ与侧压力系数有较大关系。

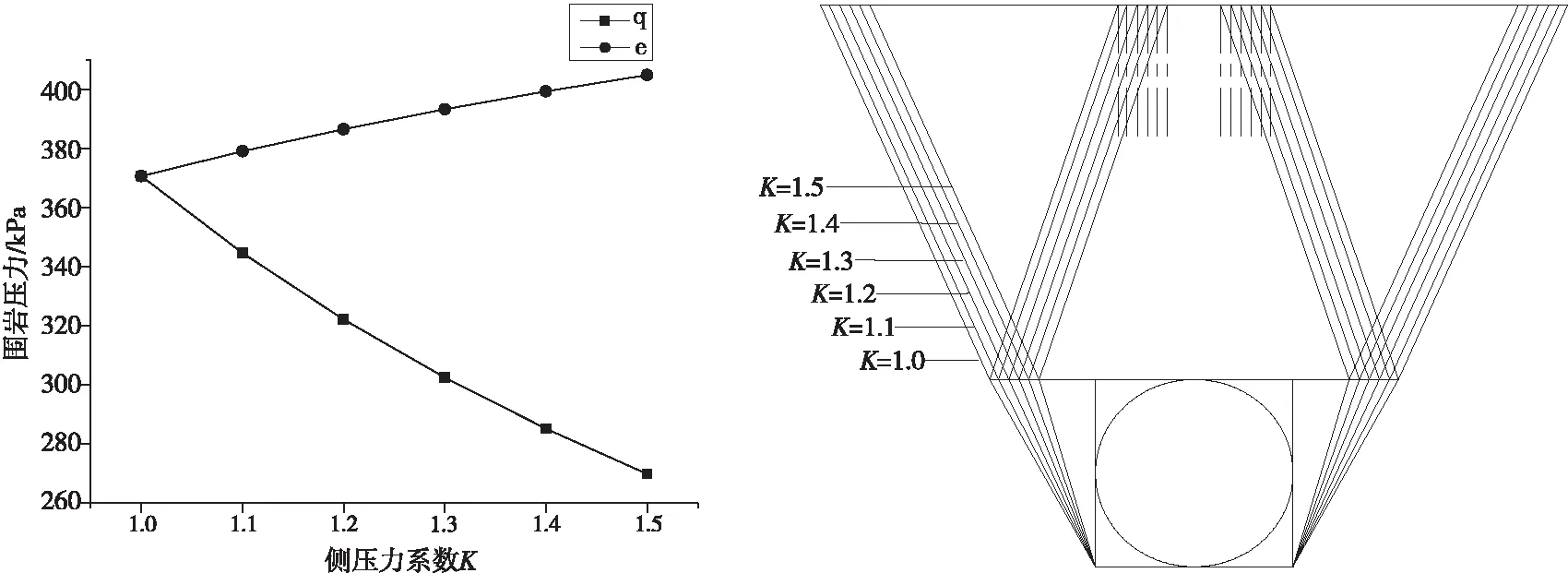
图2 支护压力与侧压力系数的关系曲线图3K对破坏模式的影响

3.3 围岩参数、隧道埋深参数分析

通过工程实际发现，不同围岩产生的初期支护结构变形不一样，除初期支护结构差异性带来的影响之外，围岩的差异性带来的影响更大。也就是说隧道的围岩参数对所需围岩支护压力产生较大的影响，同时也是设计初期支护结构力学所需参数的重要依据。取H=20 m，跨度h=10 m，围岩重度γ=20 kN/m3，讨论随着围岩参数改变，所需的围岩支护压力如图4所示。

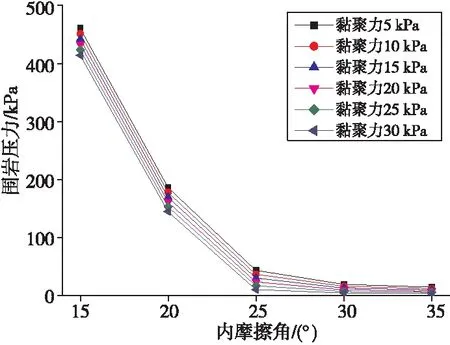
图4 支护压力与围岩参数关系

由图4可知，当内摩擦角为15°、黏聚力在5～30 kPa变化，内摩擦角较小时，所需围岩支护压力较大，即使黏聚力发生较大变化，围岩支护压力仅仅减小56 kPa，减小12.2%。随着内摩擦角的增加，围岩支护压力呈现非线性变化，并且变化趋势先快后慢，说明前期内摩擦角增大对围岩所需支护压力的减小影响较大，后期内摩擦角增大围岩支护压力变化趋于平稳，变化较小。当黏聚力为5 kPa，内摩擦角在15°～35°变化，围岩支护压力减小96.8%。因此得出：当黏聚力增大时，围岩支护压力减小不大，而内摩擦较角对围岩压力影响较大。对施工单位而言，减小初期支护所受围岩压力可选择改变围岩力学参数，通过中空锚管、超前小导管注浆等一系列措施增大围岩力学参数，减小初期支护所受围岩压力。经过超前地质预报，遇到围岩力学参数较差破碎地段，其施工阶段应予以重视，可通过短进尺开挖，尽可能降低对围岩参数的干扰，较少围岩参数降低。若通过外界方法改变周围围岩力学参数，减小围岩所需支护压力，达到安全施工目的，施工中尽可能采用砂浆等内摩擦角稍微较大的注浆材料，尽量着重改变围岩的内摩擦角参数，对于较小围岩所需支护压力具有明显效果。

取跨度h=10 m，围岩重度γ=20 kN/m3，黏聚力c=10.0 kPa，讨论随着隧道埋深、内摩擦角改变所需的围岩支护压力，如图5所示。计算中同时调用MATLAB中参数，计算出AA′长度和AA′长度小于0时，结果表明此时浅埋隧道破坏模式已不适用，计算结果不具有较大意义。

由图5～6可知，内摩擦角较小时，隧道围岩支护压力较大。以内摩擦角为15°讨论，随着隧道埋深增加，支护压力呈现先略微增加后减小趋势，这是由于支护压力所需平衡的重力增加，导致围岩压力出现略微增加。随着隧道埋深增加，隧道自然拱形成，内部耗能做功增加，所需隧道支护压力逐渐减小。随着内摩擦角增加，隧道所需支护压力急剧减小，内摩擦角为15°～30°、埋设20 m，围岩压力在451.4～15.9 kPa变化。AA′长度变化趋势如图6所示，AA′长度变化趋势与围岩压力变化趋势相似，呈现相同规律。内摩擦角为20°、埋深40 m，AA′计算长度出现小于0变化，表明已经不属于本文破坏模式讨论范畴，破坏模式出现焦点，可理解为非浅埋讨论领域。内摩擦角变为25°和30°时，可以看出，AA′计算长度出现小于0焦点的隧道埋置深度急剧减小，表明随着内摩擦角增加，且地质围岩参数较好时，隧道更易于形成自然拱现象，所需支护压力较小，同时也表明浅埋隧道、非浅埋隧道临界深度位置与围岩参数有较大关系，不同围岩参数对同一隧道而言，浅埋、深埋的区分受围岩参数影响。

取跨度h=10 m，围岩重度γ=20 kN/m3，内摩擦角φ=18°。讨论随着隧道埋深、黏聚力改变所需的围岩支护压力，如图7～8所示。

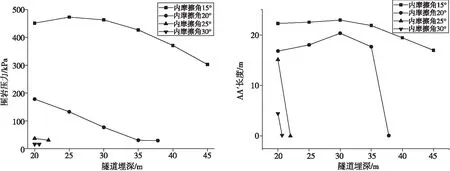
图5 隧道埋深对围岩压力影响图6 隧道埋深对AA′的影响

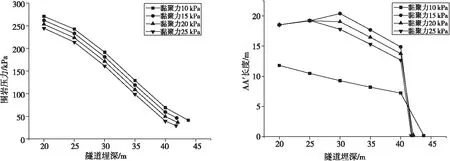
图7 隧道埋深对围岩压力影响图8 隧道埋深对AA′的影响

由图7～8可知，黏聚力增大时，隧道所需围岩支护压力较小，但对比隧道埋深变化影响，黏聚力对围岩压力影响较小。黏聚力在10～25 kPa、埋深20 m时，围岩压力变化在270.7～244.6 kPa，减小9.6%；黏聚力为10 kPa、埋深20～40 m时，围岩压力变化在270.7～69.3 kPa，减小74.4%。此外，在接近埋深45 m时，AA′计算长度小于0，可理解为此时属于非浅埋隧道。AA′计算长度随着隧道埋深增加，呈现计算长度先增加后减小的趋势。