多中心临床试验随机化竞争入组方式的探讨*

袁阳丹 刘伟杰 刘玉秀，3△ 陈丽嫦 陆梦洁 刘雅琦，3 刘 曼，3

【提 要】 目的 对于多中心临床试验随机化采用竞争入组的情形，应该共用一个随机分配序列，还是各中心使用各自的随机分配序列，目前未见研究报道。本文将通过探讨整个分配过程中以及分配完成后整体和中心内部的均衡性行为，为多中心临床试验随机化竞争入组方式的选择提供参考和实用性指引。方法 以随机化性能较好的大棒法(big stick design，BSD)作为随机化方法，通过设定不同的中心数、样本量以及最大容许不平衡例数(maximal tolerated imbalance，MTI)，借助随机模拟的方法，分析两种不同竞争入组方式下整体和中心内部的均衡性行为。结果 随着样本量的增加，各中心共用一个序列的过程均衡性变差，而选用各自序列时则保持稳定。随着中心数的增加，各中心选用各自序列的过程均衡性变差，而共用一个序列时变好；多中心共用一个序列时无法通过使用较小的MTI来减少中心内部的不均衡。中心数不是很多时，各中心使用各自序列最终出现严重不均衡的比例非常小。通过模拟可以找到各中心使用各自序列竞争入组比共用一个序列均衡性更优的最小样本量，结果表明最小样本量和中心数存在线性关系。结论 如中心数非常多，分配到各中心的例数很少时，可考虑多中心共用一个随机分配序列，但需要持谨慎的态度；其他情况，一般推荐各中心使用各自的随机分配序列。

当多中心临床试验存在各中心间入组快慢不均时，为了加快试验的入组进程，往往事先并不固定各中心的入组例数，而是采用竞争入组的方式入组受试对象。然而，对于多中心临床试验竞争入组，究竟是采用多中心共用一个随机分配序列的方式，还是多中心使用各自的随机分配序列的方式，目前未见研究报道。虽然多中心共用一个随机分配序列时最终组间的均衡性好，但各中心的均衡性难以保证，甚至会存在某中心受试对象全部被分入某组的可能。当然，多中心使用各自的随机分配序列的方式可以使得各中心内部的均衡性很好，然而整体的均衡性可能就会受到影响。如何选择两种不同的竞争入组方式具有重要的现实意义。

随机化方法及均衡性评价指标

已有研究表明，在一系列的随机化方法中，大棒法(big stick design，BSD)具有较好的随机性性能[1-2]。本文将选择BSD方法，同时考虑整体和中心的均衡性，对多中心临床试验随机化竞争入组方式进行探讨。

BSD方法是由Soares和Wu等人在1983年提出的一种仅限于两处理组平衡试验的随机化方法[3]，其条件分配概率为：

其中，dj-1表示第j-1例受试者分配之后，两处理组例数之差，即N1，j-N2，j；MTI为组间最大容许不平衡例数(maximal tolerated imbalance)。

对随机化方法均衡性评价，常用指标有分配过程中组间受试者例数差的最大值(the maximum absolute imbalance in the randomization sequence，MI)、组间例数分配相等的频率(the probability of achieving exact balance in the randomization sequence，EB)以及组间例数差的均数(the mean of the difference in treatment group sizes，DN)[2]。本文将选择DN作为均衡性评价指标，该指标越小均衡性越好。为了区分整体和中心内部以及过程和结果的均衡性，分别采用以下指标来刻画其均衡性：

①DN：整个分配过程中两组例数差的绝对值均数，反映了整个分配过程的均衡性。

②MCDN：整个分配过程中各中心两组例数差的绝对值之和的均数，反映各中心分配过程的均衡性。

③FDN：分配完成后最终整体两组例数差的绝对值，反映分配完成后最终的均衡性。

④MCFDN：分配完成后各中心两组例数差的绝对值之和的均数，反映了分配完成后各中心最终的均衡性。

随机模拟研究

1.模拟方法

采用BSD方法，分别按照多中心共用一个序列和多中心使用各自的序列两种多中心竞争入组随机分配序列的方式，进行100000次模拟。设定受试者分配到任一中心的可能性都是等概率的。

本次模拟使用SAS 9.4系统编程实现。

第一种模拟设定：了解不同中心数和样本量时过程均衡性和终末均衡性的行为。取中心数为5、10、15、20、25、30，样本量为100至1000，MTI=2，计算均衡性指标。

第二种模拟设定：了解不同MTI和样本量时过程均衡性和终末均衡性的行为。取MTI为1～5，样本量为100～1000，中心数为5，计算均衡性指标。

第三种模拟设定：了解各中心使用各自随机序列竞争入组时终末均衡性的行为。取MTI为2和3，样本量为100～1000，中心数为5、10、15、20、25、30，计算多中心使用各自的序列最终两组差值分布。

第四种模拟设定：寻找各中心使用各自序列竞争入组时，能保持过程均衡性优于共用一个序列竞争入组的最小样本量。取中心数为5～20，MTI=2，分别按照各中心使用各自序列和共用一个序列，模拟获得DN+MCDN，通过迭代寻值，得到多中心使用各自的序列优于共用一个序列的最小样本量。

2.模拟结果

(1)第一种模拟设定的模拟结果

根据模拟得到的数据，可画出图1～10。

从图1～4可看出确定中心数后，随着样本量的增大，多中心共用一个序列DN值和使用各自序列MCDN值均平稳且两者非常接近，使用各自序列DN值也趋于稳定，而共用一个序列MCDN值不断增大。如对DN和MCDN这两个指标赋予一样的权重，确定中心数后，总样本量较大时适用多中心使用各自的序列。

从图5、6可看出确定样本量后，随着中心数的增加，多中心共用一个序列DN值和使用各自序列MCDN值均平稳且两者非常接近，使用各自的序列DN值不断增大，而共用一个序列MCDN值不断减小；如对DN和MCDN这两个指标赋予一样的权重，确定样本量后，中心数较少时适用多中心使用各自的序列。

从图7、8可看出确定中心数后，随着样本量的增大，多中心共用一个序列和使用各自序列的FDN/n值都逐渐趋于0且两者越来越接近；多中心共用一个序列(MCFDN×中心数)/n值和使用各自序列(MCFDN×中心数)/n值不断减小，且后者更快收敛到0。同时考虑FDN/n和(MCFDN×中心数)/n两指标，样本量不是非常小时，多中心使用各自的序列均衡性更优。

从图9、10可看出确定样本量后，随着中心数的增大，多中心共用一个序列FDN/n值平稳且最小，而使用各自的序列FDN/n值缓慢增大。多中心共用一个序列和使用各自序列的(MCFDN×中心数)/n值都在不断增大，但多中心共用一个序列MCFDN值随着中心数增大而减小，所以其(MCFDN×中心数)/n值增大速度越来越缓慢；而使用各自序列的MCFDN值不随中心数而改变，所以其(MCFDN×中心数)/n值增大速度不变；中心数非常大时，两线相交。同时考虑FDN/n和(MCFDN×中心数)/n两指标，中心数不是非常大时，多中心使用各自的序列均衡性更优。

(2)第二种模拟设定的模拟结果

从表1可看出多中心共用一个序列时MCDN和MCFDN值随着MTI的增大没有明显的变化，模拟发现样本量100～1000均有同样的规律。可认为多中心共用一个序列时中心内部均衡性与MTI没有相关关系，所以无法通过使用较小的MTI来减少中心内部的不均衡。

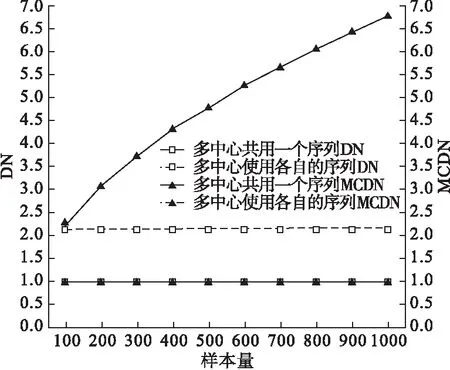
图1 样本量100～1000时均衡性指标DN与MCDN的模拟比较(MTI=2，中心数为5，模拟100000次)

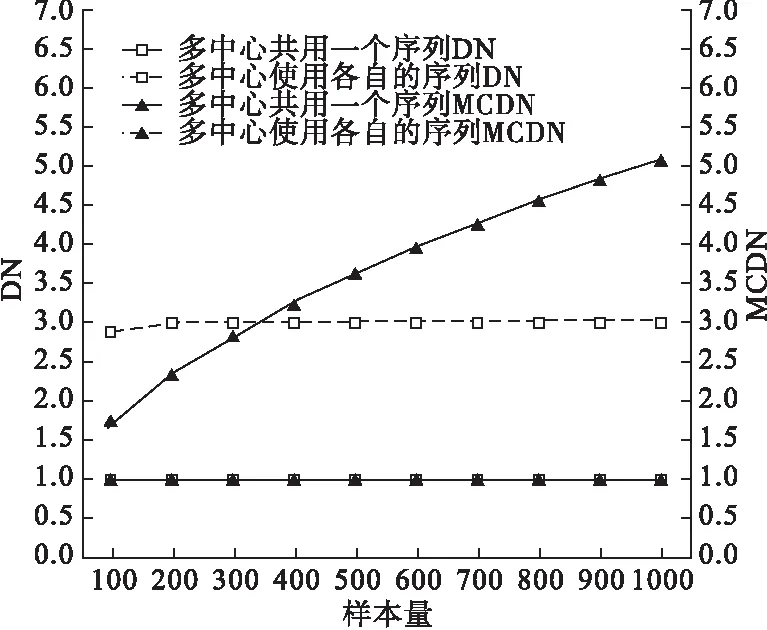
图2 样本量100～1000时均衡性指标DN与MCDN的模拟比较(MTI=2，中心数为10，模拟100000次)

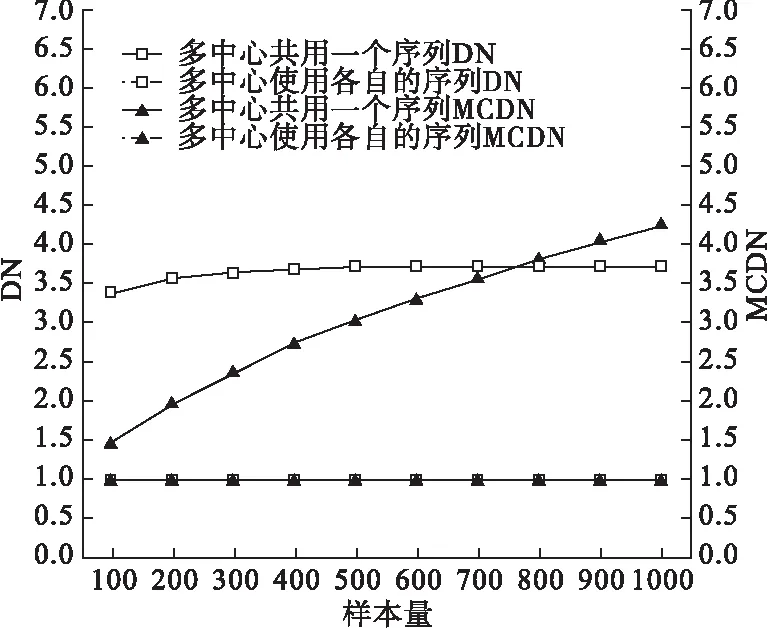
图3 样本量100～1000时均衡性指标DN与MCDN的模拟比较(MTI=2，中心数为15，模拟100000次)

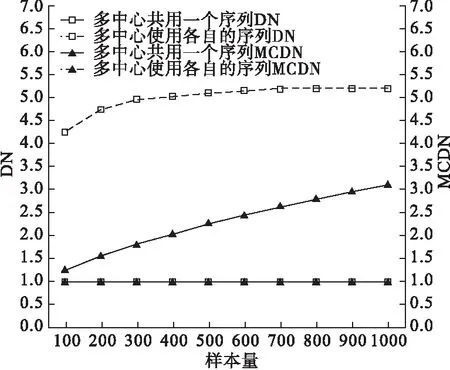
图4 样本量100～1000时均衡性指标DN与MCDN的模拟比较(MTI=2，中心数为30，模拟100000次)

图5 中心数5～30时均衡性指标DN与MCDN的模拟比较(MTI=2，样本量为100，模拟100000次)

图6 中心数5～30时均衡性指标DN与MCDN的模拟比较(MTI=2，样本量为800，模拟100000次)

图7 样本量100～1000时均衡性指标FDN/n与(MCFDN×中心数)/n的模拟比较(MTI=2，中心数为5，模拟100000次)

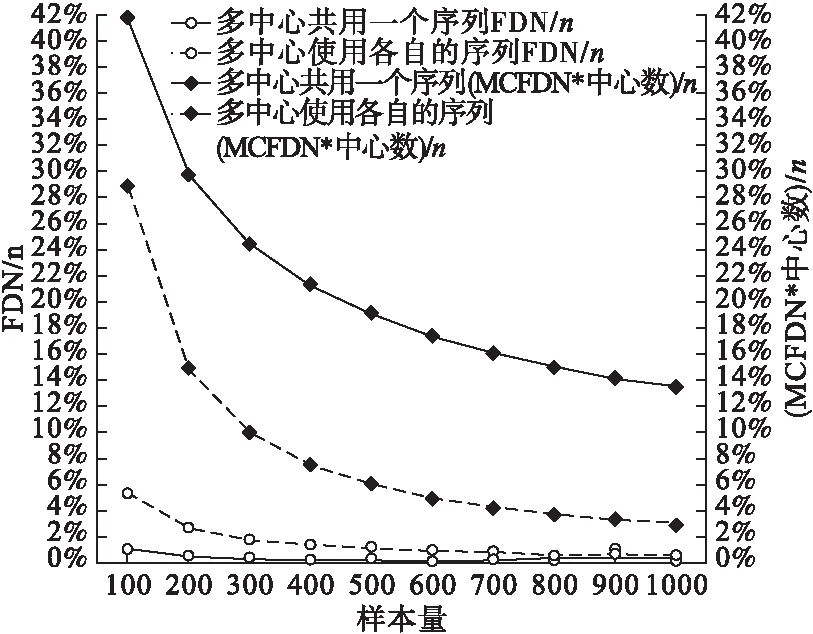
图8 样本量100～1000时均衡性指标FDN/n与(MCFDN×中心数)/n的模拟比较(MTI=2，中心数为30，模拟100000次)

图9 中心数5～30时均衡性指标FDN/n与(MCFDN×中心数)/n的模拟比较(MTI=2，样本量为100，模拟100000次)

图10 中心数5～30时均衡性指标FDN/n与(MCFDN×中心数)/n的模拟比较(MTI=2，样本量为800，模拟100000次)

表1 不同MTI下各均衡性指标比较(样本量n=1000，模拟100000次)

(3)第三种模拟设定的模拟结果

从表2可以看出，多中心使用各自的序列虽然会导致最终总体两组例数差超过共用一个序列的情形，但是对于MTI为2，总体例数差为10，中心数5至30分别包含了100%至90%的模拟样本；对于MTI为3，总体例数差为12，中心数5至30分别包含了99.98%至81.93%的模拟样本。样本量为100和1000时，多中心使用各自的序列最终两组差值分布非常接近，模拟发现样本量100～1000均有同样的规律，多中心使用各自的序列最终两组差值分布与样本量没有相关关系。

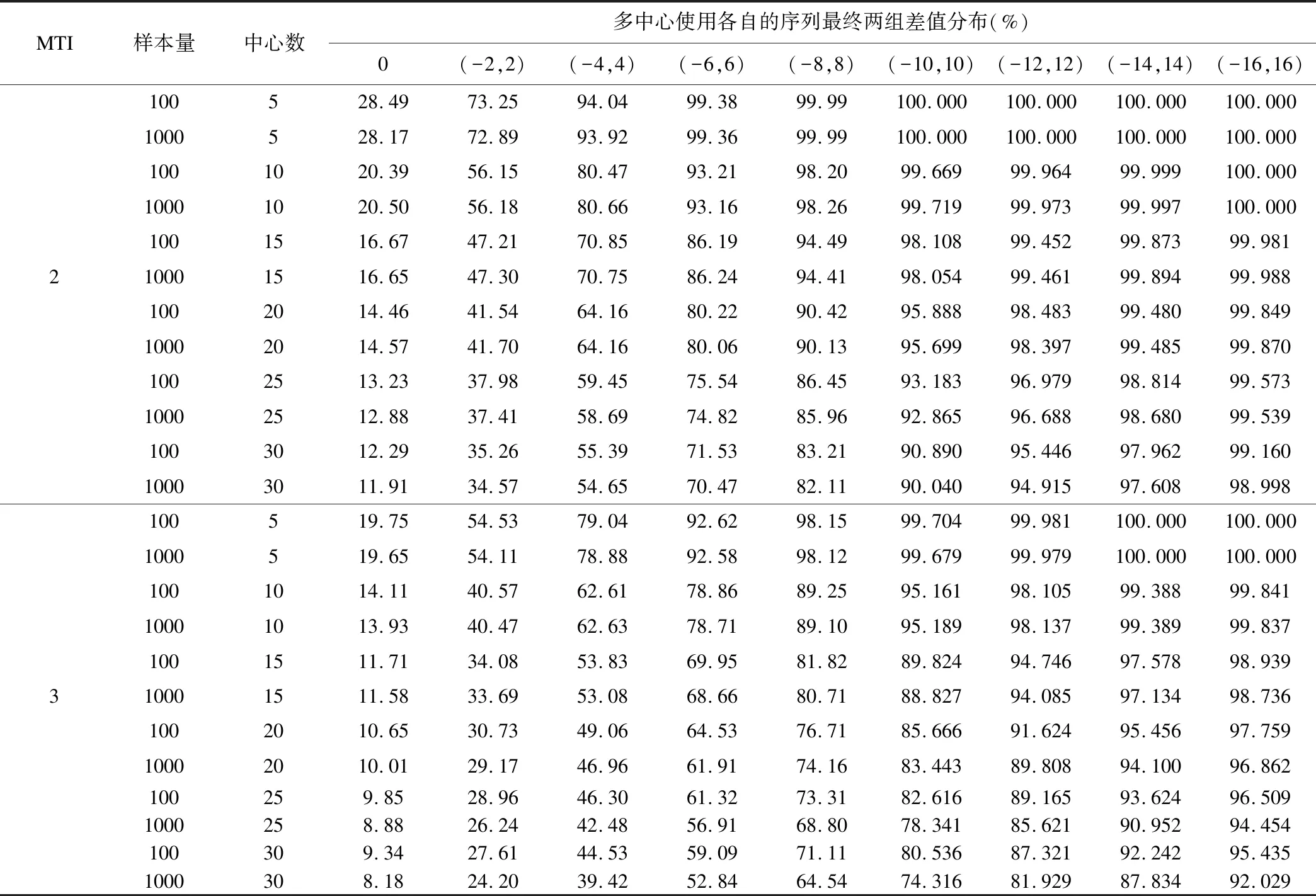
表2 BSD方法多中心使用各自的序列最终两组差值分布(模拟100000次)

样本量较大时，两组例数差几例甚至10例以上对把握度的影响是非常微小的，而多中心临床试验基本都是大样本情形。

(4)第四种模拟设定的模拟结果

表3列出了MTI为2，中心数为5～20，从整个分配过程的均衡性考虑，对DN和MCDN这两个指标赋予一样的权重，模拟得到多中心使用各自序列比共用一个序列均衡性更优的最小样本量。如中心数为5，总样本量大于等于87，多中心使用各自的序列均衡性更好。

观察发现平均每个中心样本量n和中心数C存在非常显著的相关关系(相关系数r=1)，对其可建立回归方程为

n=0.466+3.339×C

显然，总样本量N和中心数C的回归方程为

N=0.466C+3.339×C2

该方程可作为是否选择多中心使用各自序列的参考依据，即当多中心临床试验的样本量大于根据该方程推算的最小样本量时，宜采用多中心使用各自序列的竞争入组方式。

表3 BSD方法多中心使用各自的序列更优时最小样本量(模拟100000次)

结论与讨论

对于多中心临床试验随机化竞争入组方式的选择，需要同时考虑整体和中心内部的均衡性，结合中心数和样本量综合分析。本研究既考虑了整个分配过程中整体和中心内部的均衡性，又考虑了分配完成后整体和中心内部的均衡性。

如果对整体和中心的均衡性赋予一样的权重，确定中心数后，总样本量较大时适用多中心使用各自序列的随机化方式；确定样本量后，中心数较少时适用多中心使用各自序列的随机化方式。

国家药监局颁布的《药物临床试验的生物统计学指导原则》指出，多中心临床试验的各中心试验组和对照组病例数的比例应与总样本的比例大致相同，以及在多中心临床试验中，可按中心分层随机；当中心数较多且每个中心的病例数较少时，可不按中心分层[4]。然而多中心共用一个序列会引起中心内部严重的不均衡性问题，所以如果分配到每个中心的样本量不是非常少时，推荐多中心使用各自的序列。即使从整个分配过程的均衡性考虑，认为中心和整体的均衡性同等重要时，实际样本量略小于多中心使用各自的序列更优时的最小样本量，本研究也推荐多中心使用各自的序列。

如中心数非常多，分配到各中心的例数很少时，可考虑共用一个序列。然而，考虑到中心效应的存在，中心内部的不均衡很可能对最终的试验药物或医疗器械等的评价造成非常大的干扰，甚至导致根本无法评价疗效或精度的差异，所以考虑多中心共用一个序列时应该持谨慎的态度。

关于多中心使用各自的序列可能会引起最终整体两组差值较大的问题，中心不是很多时，该差值主要分布在非常小的范围；中心较多时，建议使用较小的MTI，且需要结合样本量考虑，样本量非常大可忽略此问题。

本文关于多中心临床试验随机化竞争入组方式的选择，探讨了中心数、样本量以及MTI对整体和中心内部均衡性的影响，完善了多中心随机化研究，为多中心临床试验随机化竞争入组方式的选择提供了参考和实用性指引。