工具变量的一个性质

王义闹

(温州大学数理学院，浙江温州 325035)

考虑随机解释变量问题：

其中 b0,b1为常数， x,u为随机变量，其相关系数 r(x,u ) = rxu≠0 ,E (u ) = 0 ，并有容量为n的简单随机样本(yi, xi, ui) ,i = 1 ,2,… ,n ，于是 r(xi, ui) = rxu≠0 , i = 1 ,2,… ,n ，即随机解释变量x与随机干扰项u同期线性相关.

我们知道，用最小二乘法（Ordinary Least Squares, OLS）估计模型（1）中的参数 b1，得到的是有偏的、不一致的估计量，用工具变量法（Instrumental Variable, IV）可以得到有偏的、一致估计量[1].于是只要有足够的样本，工具变量法估计值优于最小二乘法估计值的概率就足够大.工具变量法已经成为一种重要方法.本文对工具变量进行研究，证明了工具变量有如下性质：

存在

其中 ux,为（1）式中变量，使

即存在与u不相关，与x相关性最强的随机变量v（以下称为理想工具变量），且这样的理想工具变量满足

为叙述方便，以下称工具变量的这一性质为理想工具变量存在性.

以依次表示随机解释变量x与工具变量w的样本相关系数、工具变量w与随机干扰项u的样本相关系数，以 σxs, σus依次表示随机解释变量x与随机干扰项u的样本标准差，则工具变量法估计值为

最小二乘法估计值为

由理想工具变量存在性易见，x的任一工具变量w满足 ( r(x,w) )2≤1- ( r(x,u))2，这表明随机解释变量x与随机干扰项u高度相关时，任一工具变量w必与解释变量x低度相关，进而将会因为 rwus不等于0的概率为1、并且 rxws接近0的概率较大，从而由（5）式可见，工具变量法估计值bˆ1偏离真值b1较远的概率较大.

这就提示我们，当随机解释变量x与随机干扰项u高度相关时，随机解释变量x与工具变量w必然低度相关，如果样本容量不够大，要慎重应用工具变量法估计值分析问题.

另一方面，当随机解释变量x与工具变量w高度相关时，由理想工具变量存在性易见，一定很小，从而由（5）式和（6）式知工具变量法估计值优于最小二乘法估计值的概率不一定很小.如果样本容量不够大，也要慎重应用工具变量法估计值分析问题.

下面严格证明理想工具变量存在性，并通过数值模拟对工具变量法估计值与最小二乘法估计值的精度作一直观比较.为证明（2）式的存在性，先讨论两个随机变量线性相关与一元线性回归之间的关系.

1 线性相关与线性回归的一点关系

为下文引用方便，重述文[2]给出的结果.

定理1 当变量 x ,y都是随机变量，且二者线性相关系数 r ( x ,y)≠0时，必存在唯一一组常数

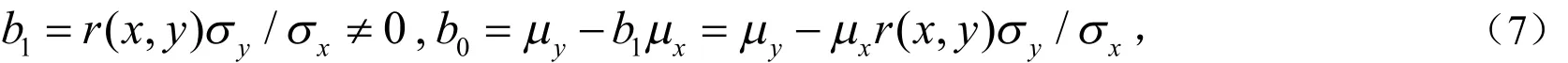
以及随机变量 xbbyu10--= ，使

证明见文[2].

定理2 设被解释变量y与随机解释变量x及随机干扰项u之间有如下总体规律：

其中 x ,u线性无关，V ar(x) = σx2≠0 ,E (u) = 0 ,Var(u ) = σu2,b1≠0，则其中常数 b0,b1及随机变量u是唯一的，且 y ,x线性相关， y ,u线性相关，相关系数为

且有 [r (y,x) ]2+ [ r(y,u)]2=1.

证明：若存在常数 c0,c1及零均值随机变量v，使 y = c0+c1x+v，且x与v线性无关，则与（1）式相减得

求x与（10）式两端的协方差得 (b1-c1)2σx2=0，由Var(x) = σx2≠0知c1=b1.于是（10）式成为 b0- c0+ u - v = 0 ，两边取数学期望，由 E ( u )= 0 =E(v)得 b0= c0，进而得 u = v .这就证明了 y = b0+b1x+u中常数 b0,b1及随机变量u是唯一的.且有

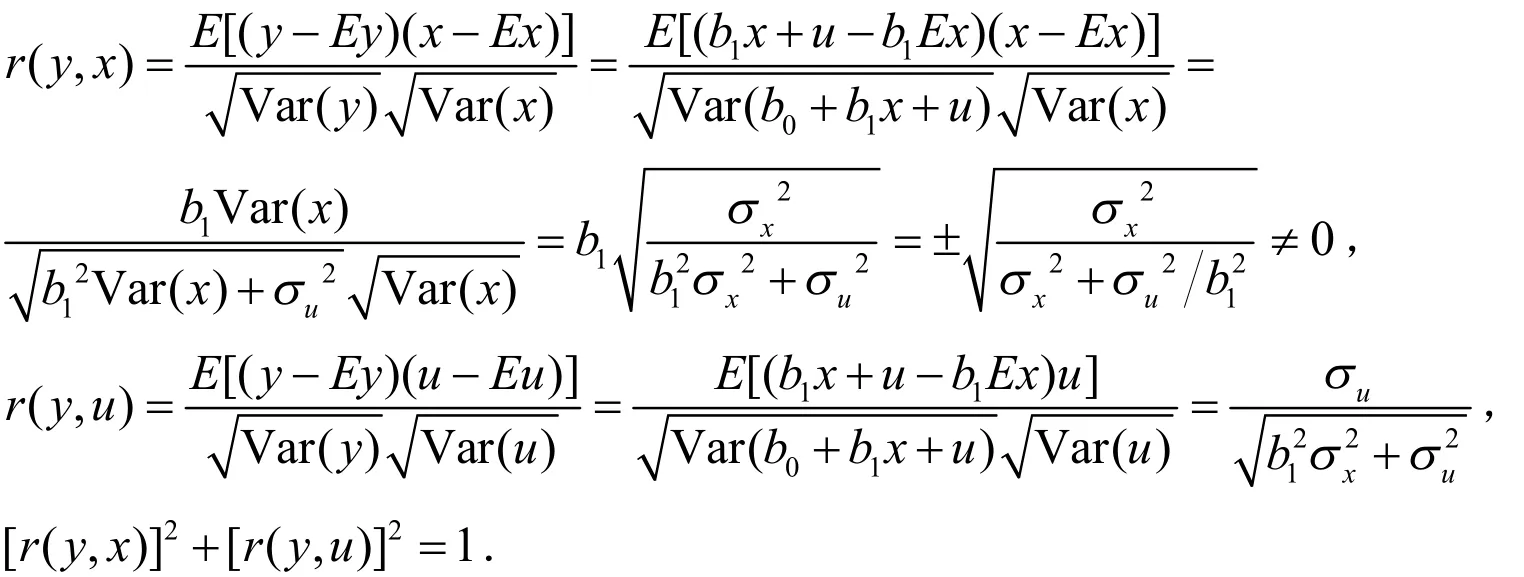
定理2表明，在解释变量是随机变量的一元线性回归问题中，在随机干扰项均值为0，解释变量方差大于0且与随机干扰项线性无关的条件下，总体规律的表达式是唯一的，且 yx,必线性相关.

定理1表明，线性相关的随机变量 yx,之间一定有形如（8）式的唯一线性表示；定理2表明随机被解释变量y与随机解释变量x满足关系式（8）且随机解释变量x与随机干扰项线性无关时， yx,之间的关系式（8）是唯一的，且随机变量 yx,之间一定线性相关，相关系数由（9）式给出.这就是线性回归分析与线性相关分析的一点联系.

2 随机解释变量问题的理想工具变量

考虑只有一个随机解释变量的问题（1）：

式中，10,bb 为常数，u为0均值随机干扰项，x与u同期线性相关（ix与iu线性相关）.理想的工具变量z是与u线性无关，与x的线性相关系数达到最大的随机变量.

由于x与u线性相关，故由定理1及u为0均值知，存在

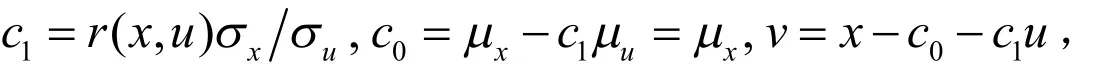
使

下面推导理想的工具变量z与x的线性相关系数的上界.由于z与x线性相关，根据定理 1可设

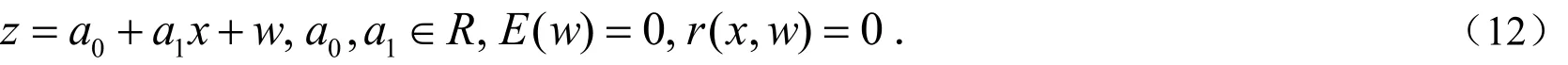
我们的目标是在满足 r ( z ,u)=0的条件下，寻找合适的 a0, a1,w，使 r ( z ,x)达到最大.由

与（11）式知， r ( z ,u)=0的条件等价于（13）式分子为0，即

亦即w与u是线性相关的，且相关系数由（14）式给出.于是由定理1及 wu, 为0均值知，存在

其中随机变量t满足 E (t ) = 0 ,r(u,t)=0.代入（11）式得工具变量z应满足

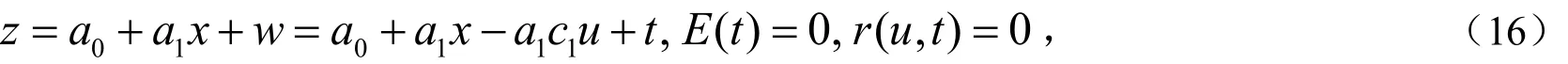
并且其中 wx,应满足

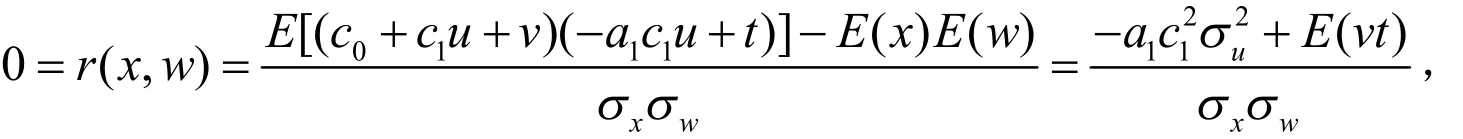
从而 tv,应满足

即 tv,必须线性相关且相关系数如（17）式.从而存在与v线性无关的随机变量s，使

由（11）式、（16）式和（18）式得

其中 d0,d1∈ R ,d1≠0.由工具变量与随机干扰项不相关的基本要求 r ( z ,u)=0以及（12）式r( u ,v)=0知，工具变量z的表达式（19）中s还应满足

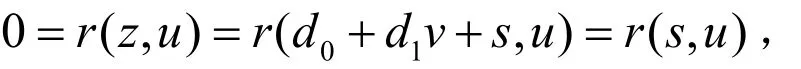
至此，我们得到工具变量z必须满足的条件为（19）式和（20）式.这样的工具变量z与x的线性相关系数的绝对值

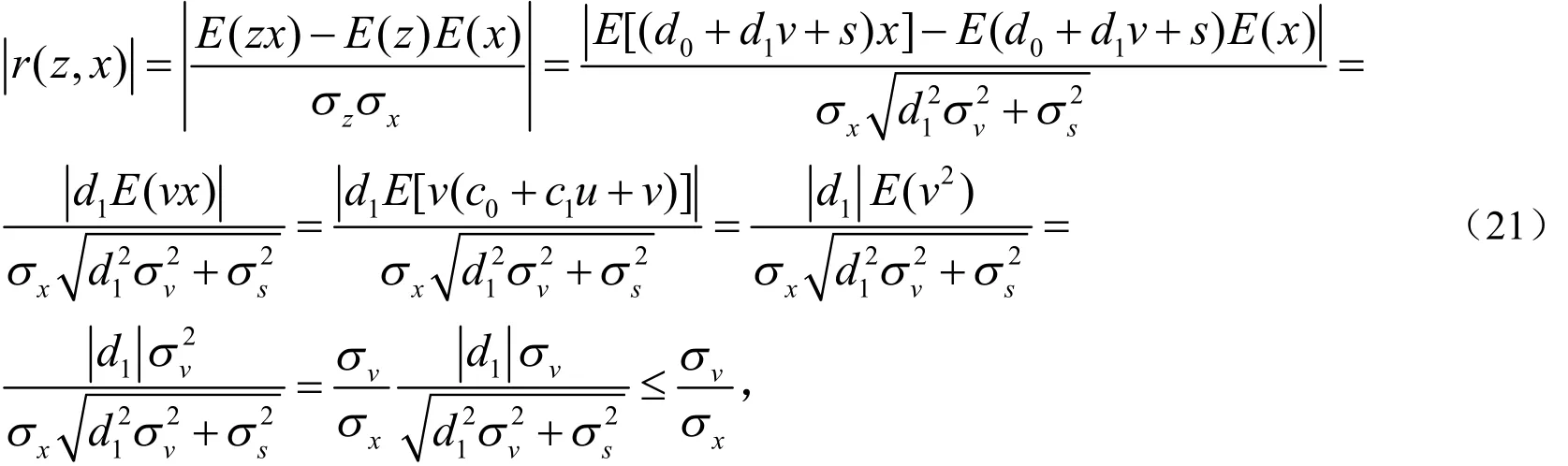
其中σs=0，即工具变量z以概率1等于（19）式中d0+d1v时，|r(z,x)|取到最大值σvσx，我们称这样的工具变量z为x的理想工具变量.特别，当 d0= 0 , d1=1时， z = v 即x中分解出的与u不相关的v就是x的一个理想工具变量.

在实际问题中，随机误差项u是观测不到的，因此x的理想分解式（11）就得不到，所以我们称 d0+ d1v为x的理想工具变量.虽然理想工具变量在现实中难以得到，但我们可以用它分析工具变量法估计量的估计效果.上面的讨论可总结成如下定理.

定理3 对只有一个随机解释变量的问题：

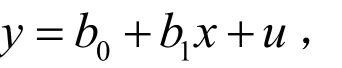
式中， b0,b1为常数，u为0均值随机误差项.对简单随机样本 { (yi,xi)｜i=1,2,…,n}，随机解释变量 xi与 ui同期线性相关.则存在 c0= μx, c1= r (x,u)σxσu,v = x - c0- c1u ，使

即x的任一工具变量z与x的线性相关系数的平方小于或等于1减去随机解释变量x与随机误差项的相关系数的平方.

（23）式表明，当随机解释变量与随机干扰项高度相关时，只存在与随机解释变量中低度相关的工具变量，不存在与随机解释变量高度相关的工具变量.例如任一工具变量z与x的线性相关系数的绝对值 r(x,z)|≤0 .1；一工具变量z与x的线性相关系数的绝对值 | r (x,z )|≤0.3；当 r (x ,u)=0.8时，任一工具变量z与x的线性相关系数的绝对值 | r (x,z)|≤0.6.另一方面，存在与随机解释变量高度相关的工具变量时，随机解释变量与随机干扰项必然是中低度相关的.例如文[1] P151例题中，随机解释变量与工具变量的样本相关系数高达0.994 295，则随机解释变量与工具变量的相关系数大于0.953 9的概率较大，进而随机解释变量与理想工具变量的相关系数大于0.953 9的概率更大，故由（23）式可知，随机解释变量与随机干扰项的相关系数绝对值小于0.3的概率较大.

由随机解释变量与工具变量的相关性可以推断随机解释变量与随机干扰项相关程度的范围.

3 工具变量法估计量与最小二乘估计量的误差的数值模拟分析

在实际问题中，我们通过定性分析可以确定随机解释变量与随机干扰项线性相关，但相关程度有多大并不清楚.虽然可以把随机解释变量与工具变量的样本相关系数作为总体相关系数的估计，进而由（23）式估计随机解释变量与随机干扰项线性相关系数的绝对值的上限，但我们仍然没办法估计下限.由（5）式（6）式可见，中小样本并且随机解释变量与随机干扰项低度线性相关的情况下，工具变量法估计值的误差很可能大于最小二乘估计值的误差.下面用数值模拟方法给出三个直观的示例来验证这一推断.

例1 为模拟随机解释变量与随机干扰项高度相关的情况，问题（1）中 b0,b1为常数，取为b0= 2 , b1=1；随机解释变量x取为服从3 + 4 × N ( 0,1)的一组容量为n的样本，记为 x1.u为0均值随机干扰项，与x线性相关，取为

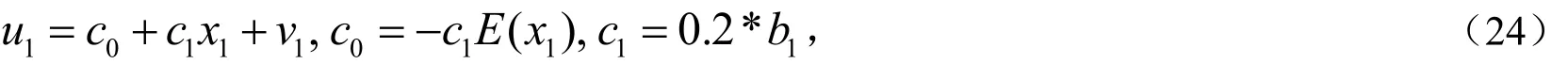
其中 v1～ N ( 0,0.12)由程序随机函数生成一组容量为n的样本，由程序生成的随机数具有良好的独立性，于是可以认为能满足 v1与 x1不相关的要求（或进一步检验独立性，符合要求就用）.则，11,xu高度线性相关；理想工具变量 v1与 x1的相关系数r(x1, v1)= 1 65 ≈ 0 .1 2403473，由定理1有

即在x取定一组观察值的条件下，理想工具变量v观察值完全由随机干扰项u的观察值所确定，最后再由

生成y的观察值.然后依次用最小二乘法、工具变量法估计参数，循环1 000次，统计估计值的均值、与设定参数值相比的均方根误差，以及工具变量法估计值更接近真值的比例，列于表1 - 3的第1 - 2行.

例2 为模拟随机解释变量与随机干扰项中度相关的情况，取

u取为 u2=-0 .6 + 0 .2x2+ v2，其中v2～ N ( 0,32)由程序随机函数生成，则 x2～ N ( 3,102)，想工具变量，为使模拟更符合实际，取工具变量2w与随机解释变量的相关系数为 0.6，可设为

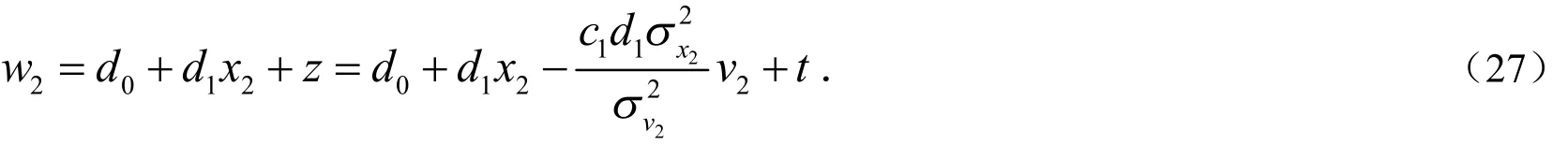
由程序随机函数生成t，则它与程序随机函数生成的 v2、 x2都线性无关，这也就满足了z与x2线性无关的要求.为满足 w2与 x2相关系数为0.6的要求，可通过适当选取（27）式中的 d1和t的方差实现：

然后依次用最小二乘法、工具变量法估计参数，循环1 000次，统计估计值的均值，与设定参数值相比的均方根误差，以及工具变量法估计值更接近真值的比例，列于表1 - 3的第3 - 5行.

例3 为模拟随机解释变量与随机干扰项低度相关的情况，取

其中u,v2线性无关，则低度线性相关.理想工具变量 v3与 x3的相关系数假定实际上取得与 x3中度线性相关的工具变量

然后依次用最小二乘法、工具变量法估计参数，循环1 000次，统计估计值的均值、与设定参数值相比的均方根误差，以及工具变量法估计值更接近真值的比例，列于表1 - 3的第6 - 10行.

表1 - 3依次列出了样本容量为10、30、100，对参数 b1=1进行1 000次模拟估计的结果：

表2 样本容量为30的1 000次模拟估计结果

表1 - 3中各行、列的意义如下：

x1ols行表示用最小二乘法和数据 x1, y1估计参数 b1=1的估计结果；

x1ivv行表示用工具变量法、理想工具变量和数据 x1, y1的估计结果；

x2ols行表示用最小二乘法和数据 x2,y2的估计结果；

x2ivv行表示用工具变量法、理想工具变量和数据 x2,y2的估计结果；

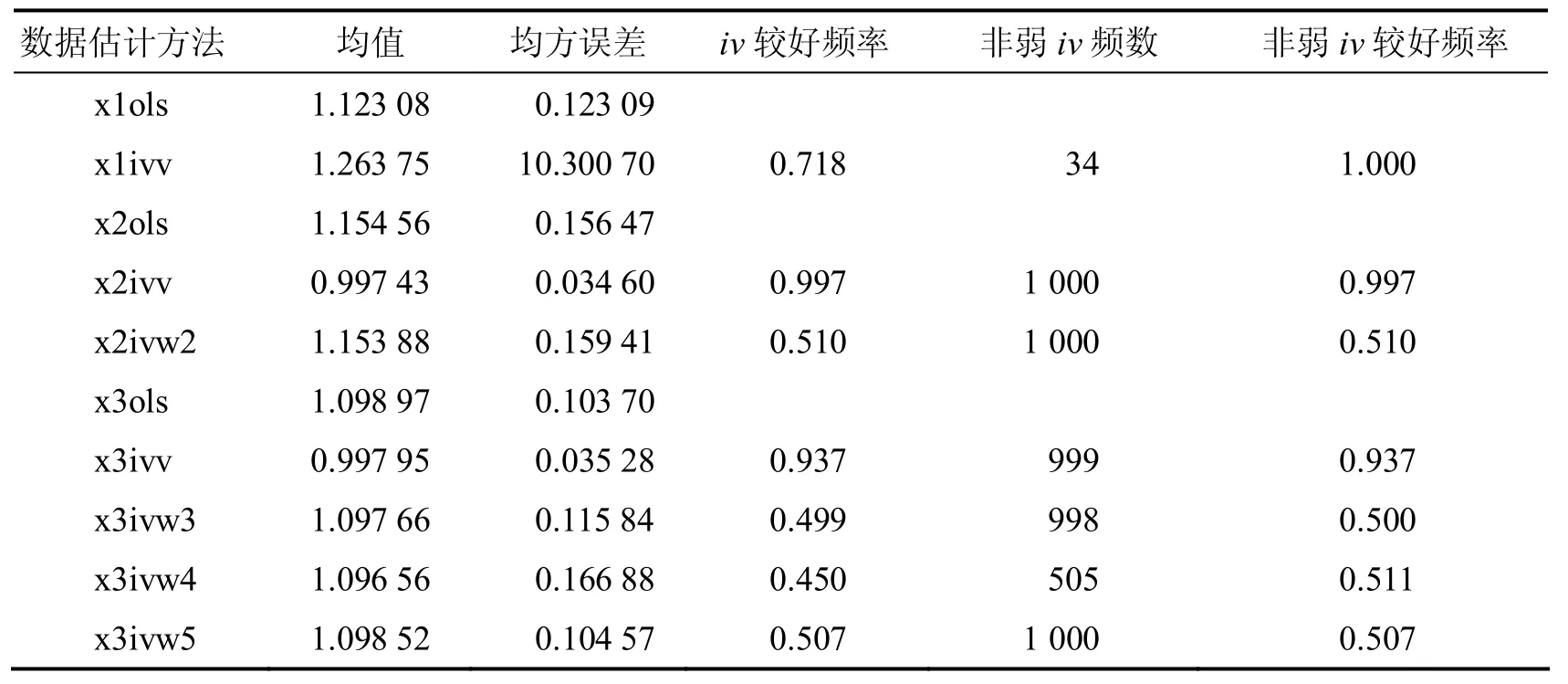
表3 样本容量为100的1 000次模拟估计结果

x2ivw2行表示用工具变量法、由（27）式生成的与解释变量的相关系数为0.6的工具变量 w2和数据 x2, y2的估计结果；

x3ols行表示用最小二乘法和数据 x3, y3的估计结果；

x3ivv行表示用工具变量法、理想工具变量和数据 x3, y3的估计结果；

x3ivw3行表示用工具变量法、由（30）式生成的与解释变量的相关系数为0.48的工具变量和数据 x3, y3的估计结果；

x3ivw4行表示用工具变量法、由（31）式生成的与解释变量的相关系数为0.30的工具变量和数据 x3, y3的估计结果；

x3ivw5行表示用工具变量法、由（32）式生成的与解释变量的相关系数为0.91的工具变量和数据 x3, y3的估计结果；

均值列表示用不同估计方法和数据估计参数 b1=1的估计值的平均值；

均方误差列表示用不同估计方法和数据估计参数 b1=1的估计值的均方误差；

较好频率列的x1ivv行表示用工具变量法、理想工具变量和数据 x1, y1估计参数 b1=1的估计值好于用最小二乘法和数据 x1, y1估计参数 b1=1的估计值的频率，其他行也是与最小二乘法比较的结果；

非弱iv频数这一列是1 000次模拟中工具变量不是弱工具变量[3]的次数；

非弱iv较好频率这一列是当工具变量不是弱工具变量时，工具变量法好于最小二乘法的频率.

模拟结果分析显示：

对表1 - 3中的x1ols行比较可见OLS估计对样本容量不太敏感，对表1 - 3中的x2ols、x3ols行比较可见同样现象.

对表1 - 3中的x1ivv行比较可见，当随机解释变量与随机干扰项高度相关时，IV估计随样本容量增大改进不明显.

对表1 - 3中的x2ivv、x3ivv两行比较可见，当随机解释变量与随机干扰项中、低度相关时，用理想工具变量估计的平均值很接近参数 b1的设定值，且随样本容量增大均方误差明显减小，体现了工具变量估计的一致性.

对同一表格的x1ivv、x2ivv、x3ivv行比较可见，当随机解释变量与随机干扰项高度相关时，理想IV估计较差，当随机解释变量与随机干扰项中、低度相关时，理想IV估计较好.

对同一表格的x2ivw2、x3ivw3两行与x2ols、x3ols两行比较可见，当随机解释变量与随机干扰项中、低度相关时，用与随机解释变量中度相关的工具变量估计的均值与OLS估计均值相近，但对不同表格比较可见，随着样本容量增大，IV估计值好于OLS估计值的频率，由明显低于0.5增大到0.5左右，均方误差明显减小.

由3个表的x3ivw4行可见，当随机解释变量与随机干扰项低度相关时，如果选用的工具变量与随机解释变量也低度相关，则在样本容量小的情况下，工具变量估计值没有参考价值；在样本容量较大（模拟实验中为100）的情况下，工具变量估计值与OLS估计值相近，IV估计值的均方误差也较小，但1 000次模拟中优于OLS估计值的次数仍小于一半.

综上可见，模拟结果显示，当样本容量不超过100时，如果选用的工具变量与随机解释变量中、低度相关，则工具变量法估计值比OLS估计值更接近设定值的频率在0.3至0.7之间.这就提醒我们，要注意检验所选工具变量与随机解释变量是否高度相关！