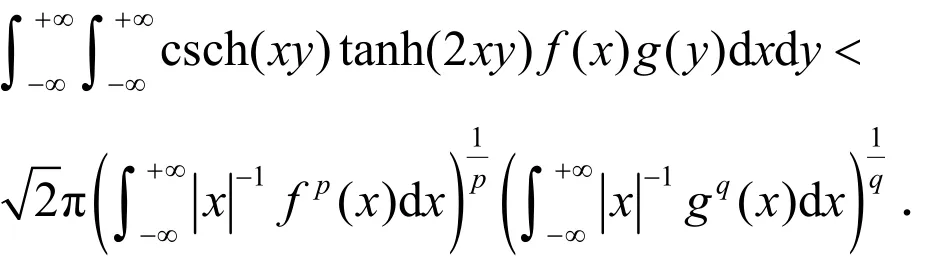一个混合双曲函数核的Hilbert型不等式

有名辉

(浙江机电职业技术学院数学教研室，浙江杭州 330053)

其中π是满足（1）式的最佳常数因子[1].不等式（1）即著名的Hilbert不等式.近十几年来，借助分析学的相关技巧，研究者们建立了大量的Hilbert不等式的类似形式及其推广[2-9]，这些不等式往往被称为Hilbert型不等式，它们在一定程度上又促进了分析学的发展.

关于核函数是双曲函数的Hilbert型不等式的研究，近些年来已有一些文献涉及[10-14]，其中文献[13]给出如下定理：

不难发现，不等式（2）中的常数因子的表达并不简洁，手工不易算出.在此，考察全平面上的核函数cosh(β x y ) sech(λ x y )，并借助正割函数的部分分式展开，建立一个全平面上的、最佳常数因子与正割函数高阶导数关联的Hilbert型积分不等式.

1 引 理

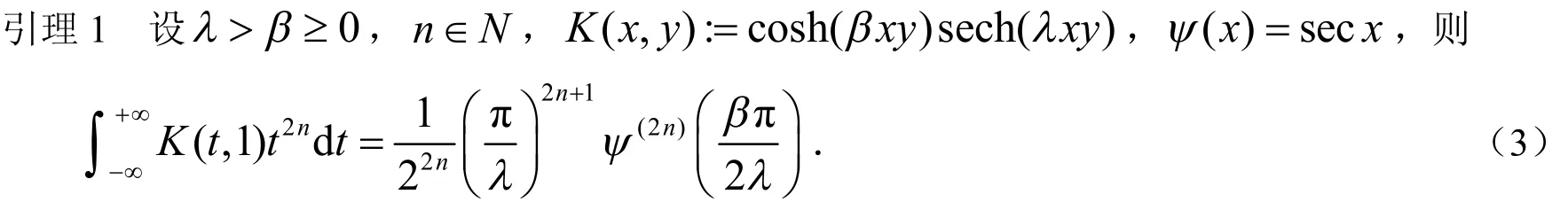
证明：

类似地，

由（5）式和（6）式可得：

同理也有：

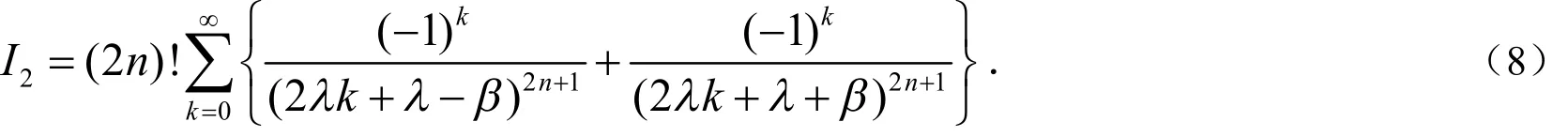
把（7）式和（8）式代入（4）式，可得：

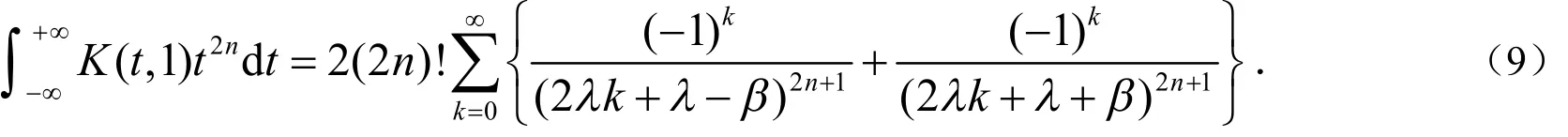
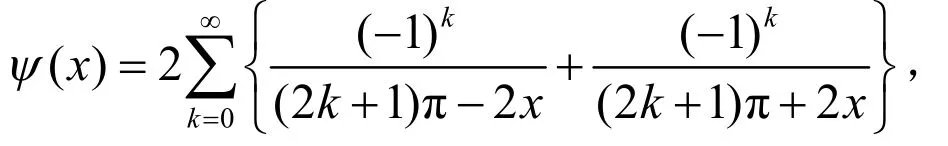
对它求(2)n阶导数得：

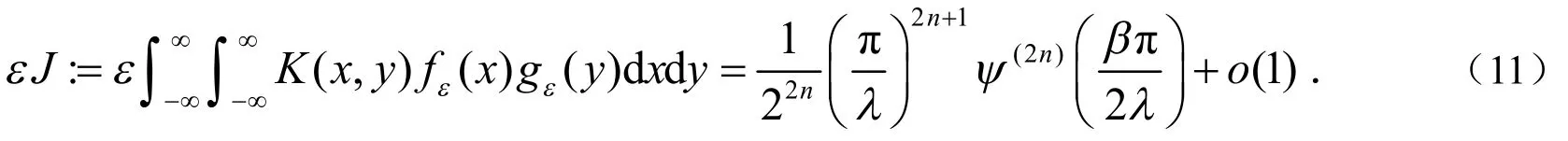
证明：

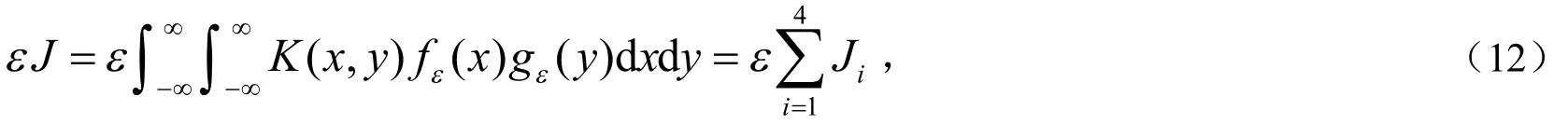
其中，

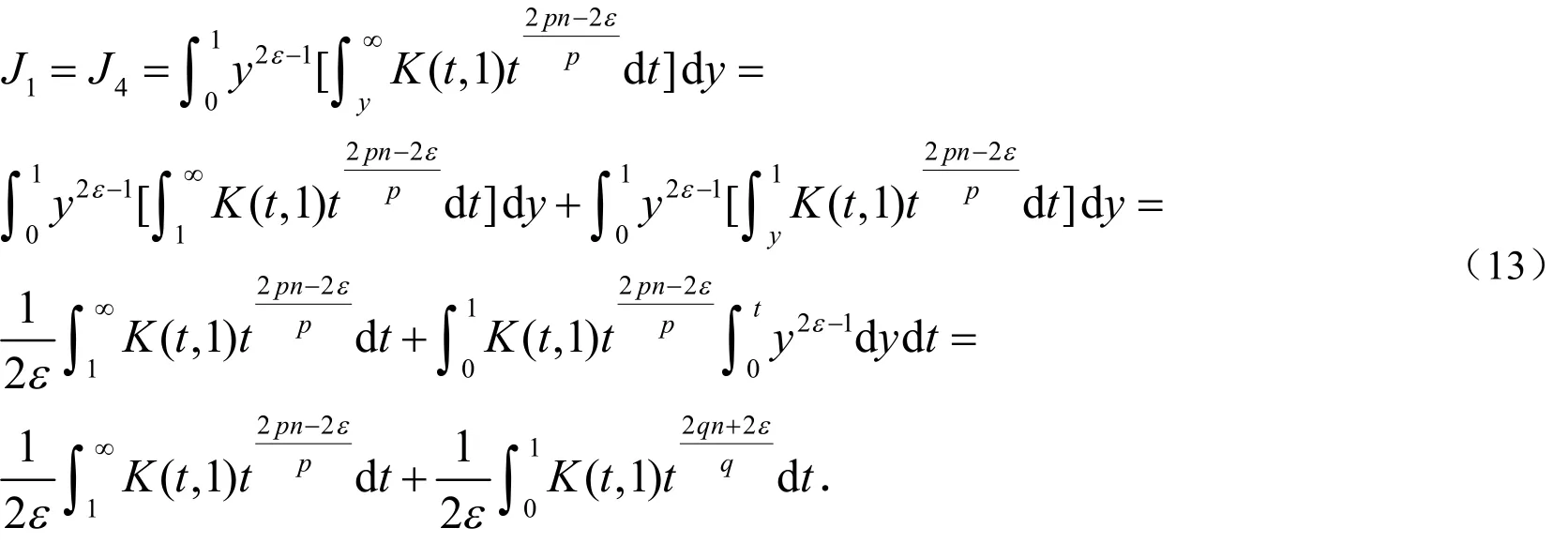
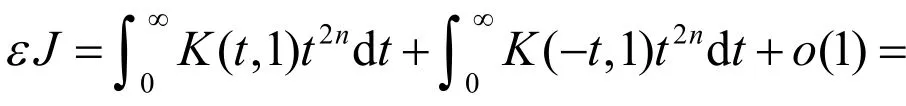
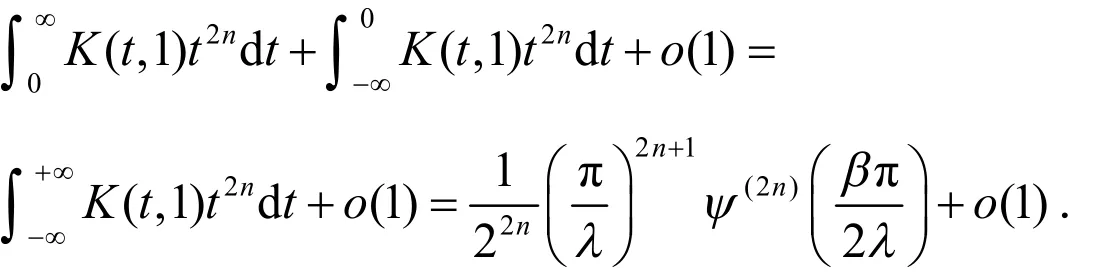
引理2获证.

2 主要结果

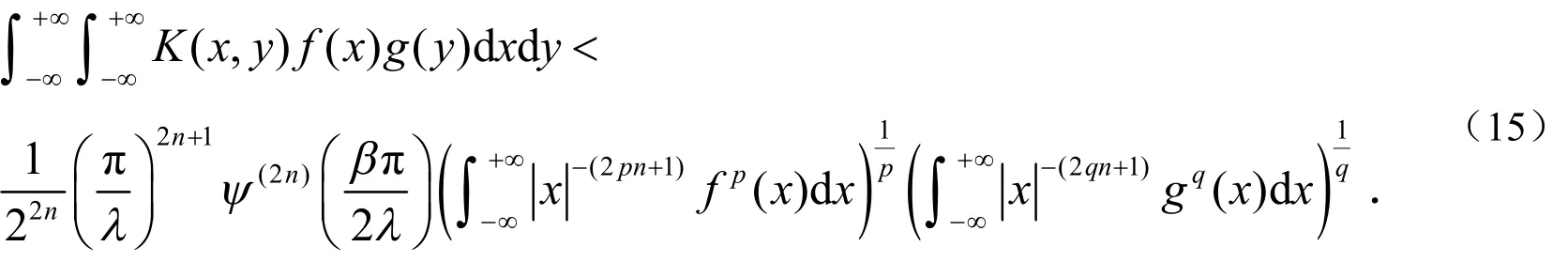
证明：由Hölder不等式和引理1，可知：

若（16）式等号成立，则有不全为零的A与B，在2R 几乎处处有[16]：

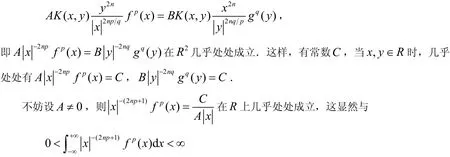
矛盾，故（16）式等号不成立.

联合（16）-（18）三式，便可得（1）式.

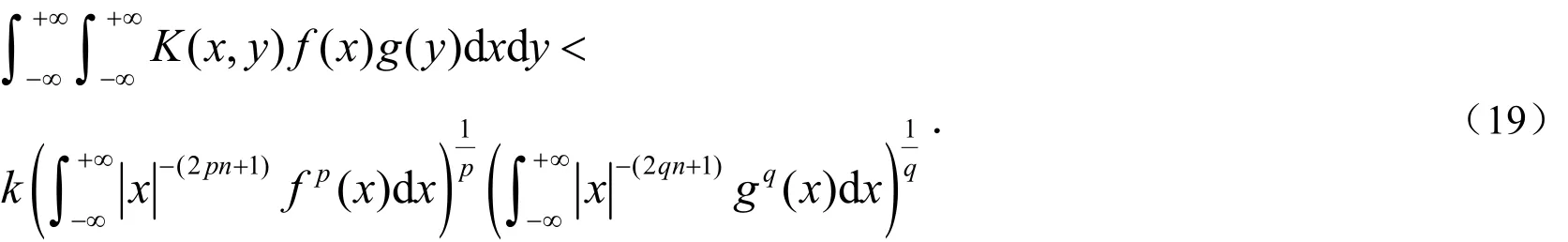
以引理2中定义的 fε(x)和gε( x)分别代替（19）式中的f和g，则

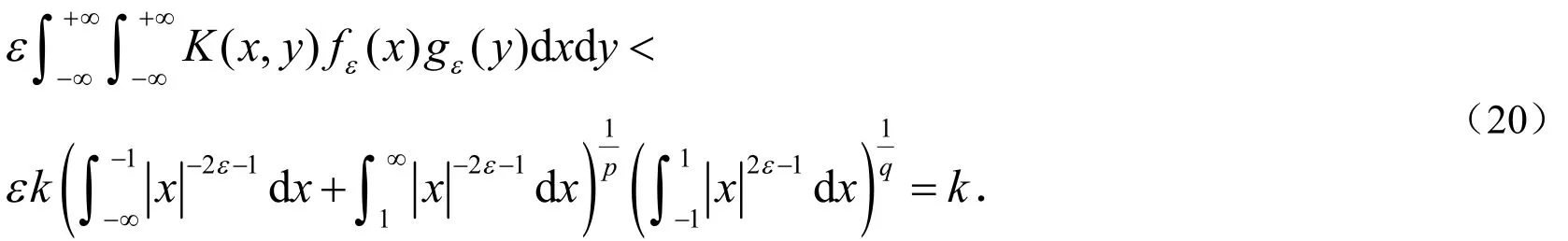
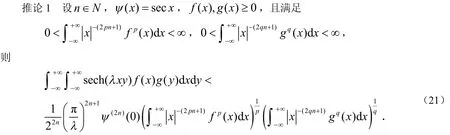
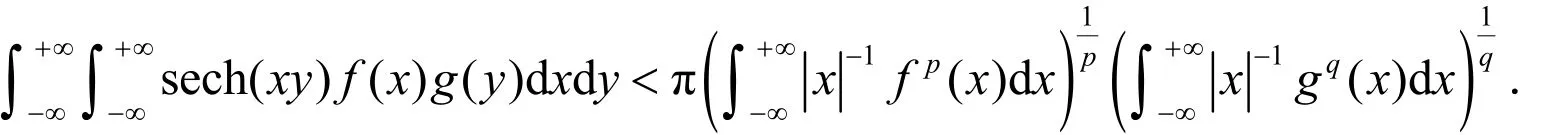
则

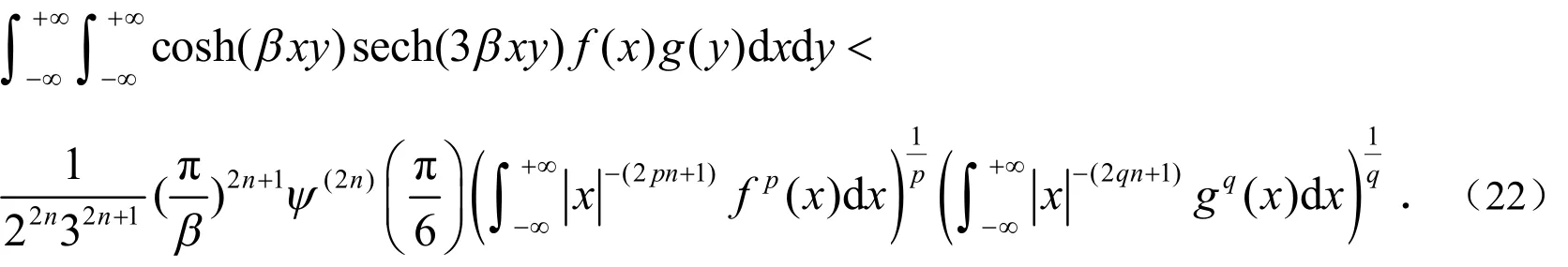
则