热力学效应对水翼云空化非定常特性的影响
2020-06-28唐庆宏于安郑源赵梦晌许哲唐魏
唐庆宏,于安,郑源,赵梦晌,许哲,唐魏
(1.河海大学水利水电学院,江苏 南京210098;2.河海大学能源与电气学院,江苏 南京211100;3.河海大学创新研究院,江苏 南京210098)
空化是一种因流体动力学因素而在液体内部或固液界面上发生的液体与其蒸气的相变过程[1],也是水力机械中不可避免的一种水动力学现象[2].水轮机[3-4]、水泵[5]、船舶螺旋桨[6]、搅拌器、喷水推进装置等均存在复杂的空化现象,并造成振动[7]、噪声[8]、空蚀[9-10]等一系列问题[11].过去1个世纪以来,对空化水动力特性的研究多是在室温水中进行的,忽略了空化的热力学效应而将其视为绝热过程[12],但蒸发吸热、凝结放热这一传热传质过程恰恰是空化的本质,伴随着空泡的初生、生长和溃灭[13].同时,水体的饱和蒸汽压力、密度等物理特性对温度变化较为敏感,此时热力学效应对空化特性的影响不可忽略[14-17].
早在1956年,STAHL等[18]就对空化流动中的热力学影响进行了研究.HOLL等[19]分别对不同温度和来流速度下水和氟利昂绕回转体空化特性开展了试验研究,测得不同工况下空化区域的温度下降数据.CERVONE等[20]对NACA0015翼型在不同攻角和来流温度下进行了空化特性试验,并指出温度升高能促进空化的产生.YAMAGUCHI等[21]进行了从室温至140 ℃的大范围变水温空化试验,并使用热敏探测器测量空化区域内的温度下降,使用∑参数评价空化的热力学效应.ZHANG等[15]提出了考虑热力学影响的空化模型,并通过CERVONE等[20]的试验进行了验证.YU等[22]在ZHANG等[15]提出的空化模型基础上进一步考虑了雷利方程中黏性项的影响,得到了更为精确的数值模拟结果.ZHU等[23]改进得到了一种新的空化模型,可用于低温流体.CHEN等[24]也提出了一种考虑热力学效应的空化模型,同时提出了C-factor用以评价热力学效应对空化的影响,指出热力学效应的拐点温度约为370 K±1 K.
实际工程中,部分水力机械运行在高温或低温水介质中,热力学效应的影响较常温水中更为显著.为了进一步探究温度对水翼云状空化非定常动态特性的影响,文中通过二次开发,将考虑热力学效应的空化模型引入商业软件ANSYS CFX 17.0中进行非定常模拟,并将空化的影响引入能量方程源项中,对源项进行修正.文中采用均相流模型和基于密度修正的湍流模型(DCM),将水体考虑为不可压缩流体,对不同温度(279,298,318 K)下绕水翼(攻角α0=8°)进行云状空化非定常模拟.
1 控制方程和数值方法
1.1 控制方程
文中采用目前使用最广泛的均质平衡流模型.计算中,连续性方程、Favre平均的N-S方程、考虑空化的能量方程及液相输运方程如下:
(1)
(2)
(3)
(4)
μeff=μm+μtur,
(5)
(6)
ρm=ρl(1-αv)+ρvαv,
(7)
μm=μl(1-αv)+μvαv,
(8)

1.2 空化模型
空化模型用以描述蒸发和凝结过程.文中采用的空化模型[25]考虑了热力学效应,模型方程如下:
(9)
(10)
式中:M为摩尔分子质量,g/mol;Rv为气体常数,Rv=461.6 J/(kg·K);rb为空泡半径;T为当地温度;pv为饱和蒸汽压力;p为当地压力;Cc,Ce分别为凝结、蒸发系数,Cc= 0.01,Ce= 0.13.
对单个空泡温度边界层应用傅里叶定律,有
(11)
Kl=λlρlCl,
(12)
式中:q为单位面积的热流量,J;ΔT为空泡内温度与周围环境温度之差;Kl为热导率,W/(m·K);λl为热扩散率,m2/s;Cl为水的比热容,J/(kg·K).
假设空泡的生长或溃灭只由蒸发和凝结过程控制,根据能量守恒定律,有
(13)
结合式(11)—(13)得
(14)
式中:C0取为翼型的弦长,C0=0.07 m;u∞为来流速度,u∞=7.8 m/s;t∞为参考时间.
考虑到湍动能会对流场空化产生重要影响,将其引入饱和蒸汽压力的数值计算中,即
(16)
ptur=0.39ρmk,
(17)
式中:k为当地湍动能.
液相、气相的密度与温度满足
(18)
(19)
式中:Rl为液体常数,Rl=472.27 J/(kg·K);Tc为温度常数,Tc=3 837 K;pc为压力常数,pc=1 944.61 MPa.
1.3 基于密度修正的湍流模型
由于标准k-ε模型会对空化区域的湍动黏度进行过度预测,因此文中采用基于密度修正的湍流模型(DCM)求解,对标准k-ε模型中的湍动黏度进行修正.空化区域内含有大量水蒸气,是一种水气混相介质.考虑到气液混相的可压缩性及其对湍动黏度的影响,对混合密度与湍动黏度进行修正,即
(20)
(21)
湍流模型中其他参数仍与标准k-ε模型保持一致.式(21)中的n值直接反映气液混合区域的当地可压缩性,会对计算结果产生重要影响.文中采用最普遍的n值,取n=3.
1.4 计算区域和边界条件
计算区域与模型试验尺寸保持一致.图1为计算域的几何结构,其中,翼型前缘距计算域进口230 mm,翼型尾部距计算域出口400 mm,翼型距计算域顶部和底部均为95 mm.翼型攻角8°,其弦长70 mm;展向厚度21 mm,即翼型弦长的0.3倍.

图1 数值计算区域与边界条件Fig.1 Computational domain and boundary conditions
文中采用速度入口边界条件u∞= 7.8 m/s,压力出口边界条件pout;上下壁面为自由滑移边界条件,前后设置为对称面;模型表面设置为无滑移、绝热壁面.空化数σ定义为
(22)
式中:T∞为参考温度.
图2为翼型周围网格分布细节.文中采用C型网格划分技术,计算域总节点为150万.为精确求解空化流场的非定常特性,本次计算时间步长取为0.000 1 s,并采用求解精度较高的双精度格式进行迭代求解.定常空化流场计算时以无空化流场作为初始值,非定常计算时以定常空化流场作为初始值.

图2 翼型周围网格Fig.2 Computational grids around hydrofoil
2 结果与讨论
2.1 热力学效应对空泡非定常变化的影响
为了探究不同温度下空泡动态特性演变的差异,数值求解得到气相等值面、气相体积分数αv和温度T在1个准周期内的变化云图[25],如图3所示.

图3 279 K下云状空泡形态变化试验与数值模拟对比图(u∞=7.8 m/s,σ=1.00,α0=8°)
Fig.3 Comparison between experimental and numeri-cal results for cloud cavitation evolution at 279 K(u∞=7.8 m/s,σ=1.00,α0=8°)
图4为279.0,298.0,318.0 K温度下,1个空泡演变周期内整个计算域空泡体积V随时间变化的曲线.文中所使用的热力学空化模型和基于密度修正的湍流模型(DCM)准确预测了空泡的初生、生长、脱落、溃灭等过程,与试验中空泡演变过程一致.此外,试验记录空泡的演变周期为56 ms,数值模拟求解得到的周期约52 ms.从空泡形态可知,由于文中所用的湍流模型提前预测了空泡的断裂和溃灭,因此演变周期缩短,而且捕捉到的空泡半径略小于试验结果.随着来流温度的升高,空化区域变得更加模糊[20,24];试验中也捕捉到了这一特性:当温度由279.0 K增至298.0,318.0 K时,空化区域亮度不断降低,空化边界更加模糊.数值模拟结果与试验结果一致,即随着来流温度的升高,空化区域的气相体积分数逐渐降低,空化区域变得更加模糊.

图4 数值模拟空泡体积随时间变化曲线Fig.4 Cavity volume versus time of numerical results
图5为298.0 K温度下试验与数值模拟空泡形态对比图[25].

图5 298 K下云状空泡形态变化试验与数值模拟对比图(u∞=7.8 m/s,σ=1.00,α0=8°)
Fig.5 Comparison between experimental and numeri-cal results for cloud cavitation evolution at 298 K(u∞=7.8 m/s,σ=1.00,α0=8°)
图6为饱和蒸汽压力pv随温度变化曲线,从图中可见,随着温度的升高,d[pv(T)]/dT逐渐增大,即水的饱和蒸汽压力对温度的变化更加敏感.随着温度的升高,附着空泡区域蒸发吸热使当地饱和蒸汽压力降低,从而对空化产生抑制作用.时素果等[25]通过分析试验结果指出:随着水温的升高,在相同空化数下,云状空泡区域减少、长度缩短.但CERVONE等[20]的试验表明:随着温度的升高,在相同空化数下,片状附着型空泡的长度和厚度均增大.CHEN等[24]对这一现象做出了解释,指出密度比例ρl/ρv和热力学效应共同影响空泡的动态特性;当温度低于370.0 K±1.0 K时,ρl/ρv的影响大于热力学效应,对空泡的产生起促进作用.由于云状空泡尺度大、非定常特性强、影响因素复杂,因此很难实际测量热力学效应对空泡尺度的影响.而试验及数值模拟结果表明:随着温度的升高,空化区域变得更加多泡和模糊,其内部气相体积分数降低.

图6 饱和蒸汽压力与温度对应关系曲线Fig.6 Saturation pressure-temperature curve of water
空化的本质是相变,包括蒸发吸热与凝结放热2个传热传质过程,使空化区域存在有限的温度梯度.图3,5,7分别为不同来流温度下翼型周围温度场的分布云图[25].流场的最大温降约0.2 K,接近YAMAGUCHI等[21]试验中捕捉到的最大温降0.3 K,验证了数值求解的准确性.从图5中可以看到,翼型周围的温度变化形态与空泡的演变形态基本一致,温降主要集中在附着空泡区域,与空化初生所致的蒸发吸热直接关联.断裂、脱落空泡的溃灭(凝结放热)会造成流场温度的升高;从图5中可知,温升主要集中于附着空泡尾部,脱落空泡区域温升不明显.随着温度的升高,空化区域温度大幅下降,导致当地饱和蒸汽压力下降,抑制空化区域的扩大,促使空泡提前断裂,同时附着型空泡变薄.

图7 318 K下云状空泡形态变化试验与数值模拟对比图(u∞=7.8 m/s,σ=1.00,α0=8°)
Fig.7 Comparison between experimental and numeri-cal results for cloud cavitation evolution at 318 K(u∞=7.8 m/s,σ=1.00,α0=8°)
2.2 热力学效应对空泡半径的影响
随着来流温度的升高,空化区域气相体积分数降低,边界更加模糊.图8为不同来流温度下空泡半径的演变云图.由于翼型下表面为低压区,属于空化的初生发展区域,加之附着空泡内部靠近壁面处气相体积分数高,因此,空泡的生长不受外部高压流场的限制.从图8中可以看出,近壁面处空泡半径大;远离壁面处由于空泡生长受外部高压流场的抑制,空泡半径较小.随着来流水温的升高,空泡半径逐渐变小,更加细密的空泡扩散加剧,从而使空化区域气相体积分数降低,空化区域及其边界变得更加模糊.

图8 不同温度下空泡半径演变云图(u∞=7.8 m/s,σ=1.00,α0=8°)
Fig.8 Evolution of bubble radius at different water temperatures (u∞=7.8 m/s,σ=1.00,α0=8°)
2.3 热力学效应对当地空化数的影响
在远离空化区域,流场温度保持恒定,热力学效应对其几乎没有影响;而在空化区域,由于受到蒸发吸热及凝结放热过程的影响,空化区域发生有限的温度降低和升高,进而直接影响到水体的物理性质,如饱和蒸汽压力pv(T)、水体密度ρl(T).因此,在准周期内的空化进程中,空化数并非保持恒定值(σ=1.00),而应是以温度T为变量的函数σ(T),即当地空化数.考虑到热力学效应对空化的影响,应采用σ(T)更准确地描述空化发生阶段.根据当地温度下的饱和蒸汽压力和密度,可得
(23)
图9为3种不同温度下σ(T)在1个准周期内的动态演变云图.从图中可以看出,随着来流温度的升高,σ(T)的变化幅度|σ(T)-1.00|也在增大.这是因为随着温度的升高,水体饱和蒸汽压力pv(T)对温度变化更为敏感,即d[pv(T)]/dT随着温度的升高而增大,即相对于同等温度降ΔT,温度越高,饱和蒸汽压力pv(T)下降得越多,σ(T)升高也越多.故318.0 K温度下的附着空泡明显小于室温298.0 K下的附着空泡.同时,在附着空泡尾部,由于空泡的断裂、溃灭等过程,空泡凝结放热,造成局部水体温度升高,导致pv(T)增大、σ(T)降低.蒸发吸热造成的空化数升高约0.10,凝结放热导致的空化数降低约0.05.而来流温度越高,pv(T)及σ(T)的变化幅度就越大,所以,318.0 K温度下脱落空泡区域和脱落空泡尺度明显大于279.0,298.0 K温度下对应的尺度.
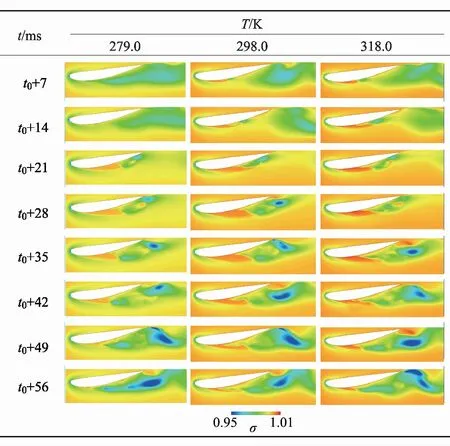
图9 当地空化数准周期性动态演变(u∞=7.8 m/s,σ=1.00,α0=8°)
Fig.9 Evolution of local cavitation number in a quasi-cycle (u∞=7.8 m/s,σ=1.00,α0=8°)
3 结 论
文中使用考虑热力学效应的空化模型和基于密度修正的湍流模型(DCM)对不同水温(279.0,298.0,318.0 K)下翼型云状空化进行了非定常数值模拟研究,旨在探究热力学效应对空化非定常动态特性的影响,得到如下结论:
1) 翼型周围的温度变化形态与空泡的演变形态基本一致,最大温度降约0.2 K;温度降低区域主要集中在附着空泡区域,与空化初生而导致的蒸发吸热直接关联.随着来流水温的升高,空泡断裂提前,附着性空化区域变薄.
2) 从空泡半径的角度解释了热力学效应对空化发展的影响,空泡半径的演变规律与试验和数值模拟中空泡形态的演变规律一致.随着来流水温的升高,空泡半径减小,空泡扩散加剧,空化区域及其边界变得更加模糊.
3) 采用当地空化数σ(T)来描述空化发生阶段,可以更准确地反映热力学效应对空化的影响.σ(T)可以更直观地反映流场温度变化对空化发展阶段的影响,蒸发吸热造成的空化数升高约0.10,凝结放热导致的空化数降低约0.05;随着来流水温的升高,脱落空化区域扩大.
