不同参数对双浮体波能装置水动力特性的影响

纪仁玮，盛其虎*，王树齐，张玉全，张亮

(1.哈尔滨工程大学船舶工程学院，黑龙江 哈尔滨 150001;2.江苏科技大学船舶与海洋工程学院，江苏 镇江 212001;3.河海大学能源与电气学院，江苏 南京 211100)

随着经济的飞速发展，能源需求日益增大，同时也造成了能源短缺和环境污染[1-2].可再生能源的开发迫在眉睫，波浪能作为一种重要的海洋可再生能源，具有巨大的开发前景.波能装置结构形式多样，其中振荡浮子式双浮体波能装置具有结构简单、能量转换效率高和频率响应范围宽等优点[3-4]，引起了国内外学者的关注.THOMAS等[5]探究了考虑波浪作用下浮体间的相互干扰；ERIKSSON等[6]引入线性PTO (power take off)的影响，分析了坐底式单浮体波能装置的水动力特性；BABARIT等[7]通过引入黏性修正的方法，探究了流体黏性对单浮体水动力性能的影响；NAZARI等[8]研究表明，阻尼系数和自身的固有频率对浮子垂向位移影响较大.国威等[9]引入非线性PTO的影响，探究了单浮体波能装置的水动力特性.

综上所述，目前研究主要集中在单浮体波能装置，而双浮体波能装置的研究还处于起步阶段.文中首先介绍多浮体计算的基本理论.然后提出基于势流理论的ANSYS-AQWA方法，通过Fortran的二次开发，引入PTO影响，对振荡浮子式双浮体波能装置进行模拟，将计算的结果与NREL(national rene-wable energy laboratory)的试验进行对比验证.最后详细探究波浪参数、发电装置参数以及PTO参数对双浮体波能装置功率特性的影响.

1 基本理论和方法

根据线性频域分析方法，多浮体流场的总速度势φ(x,y,z)由入射势φ0(x,y,z)、辐射势φj(x,y,z)(j=1，2，…，6)和绕射势φ7(x,y,z)构成.入射势φ0(x,y,z)已知，求解总速度势φ(x,y,z)的关键是求解辐射势φj(x,y,z)(j=1，2，…，6)和绕射势φ7(x,y,z)[10].辐射势和绕射势可通过自身满足的控制方程和定解条件求解，从而可得流场的总速度势.

(1)

频域运动方程为

(2)

频域分析法得到的水动力系数借助快速傅里叶变换(FFT)转化为时域运动方程中的水动力参数.时域计算方法可以求解浮体受力与运动位移的非线性关系.时域计算方法分为直接法和间接法，其中间接时域方法应用较广.将浮体的运动等价于一系列脉冲运动的叠加，浮体的受力等价于一系列线性力的叠加，从而建立浮体运动方程[10]为

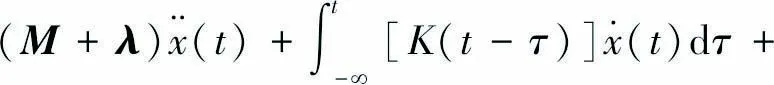
(3)

式中：M为浮体的广义质量矩阵；λ为附加质量矩阵；K(t-τ)为系统的延迟函数；C为浮体结构的静水回复刚度；F(t)为浮体受到的广义力矩阵.

2 双浮体波能装置的数值验证

2.1 模型的建立

上浮子和下浮筒构成了双浮体波能装置[11]，相关参数如表1所示，表中G为重心位置；H为浮子吃水深度.图1为双浮体模型示意图.

表1 浮子和浮筒的参数Tab.1 Parameters of upper buoy and lower buoy

图1 双浮体模型示意图Fig.1 Schematic diagram between double-floating-body model

2.2 数值验证

目前双浮体波能装置的研究有以下难点：① 浮子和浮筒之间的水动力干扰；② 浮子和浮筒之间PTO装置的影响；③ 垂荡阻尼板的影响.文中基于势流理论，通过Fortran的二次开发，引入PTO的影响，对双浮体波能装置进行时域计算分析.为验证其正确性，选取文献[12]中的算例，波高为2.5 m的规则波，引入质量-弹簧-阻尼系统来模拟PTO的影响，PTO参数中弹簧刚度为20 kN/m，阻尼为1 200 kN·s/m.模拟中改变波浪周期，时间步长0.5 s，计算500 s.垂荡运动幅值Ah的结果对比如图2所示.

图2 不同波浪周期下双浮体波能装置数值结果与试验结果的对比
Fig.2 Comparison of numerical results and experimental results of double-floating-body wave energy converter under different wave periods

图2中浮子与浮筒的相对运动的数值结果与试验吻合较好，均在T=8s时达到最大.浮子的垂荡运动幅值在T=10s时达到最大.浮筒垂荡运动幅值随波浪周期的增大呈现“先增大后平稳”的趋势.

发电功率是波能装置的重要指标.图3为不同PTO阻尼系数下双浮体波能装置的功率P随波浪周期的变化.由图中可以看出：① 阻尼系数为1 200 kN·m/s时，数值结果和试验结果趋势吻合较好，共振周期处的误差主要由于忽略黏性效应以及试验误差所导致；② 不同PTO阻尼系数对应着不同的共振周期和最优吸收功率.

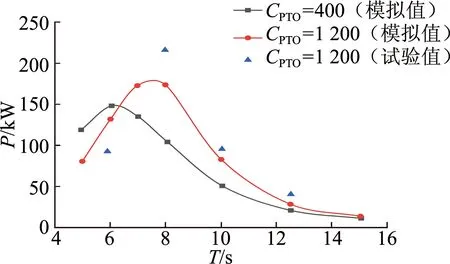
图3 不同波浪周期下双浮体波能装置的功率特性Fig.3 Power characteristics of double-floating-body wave energy converter under different wave periods

3 双浮体波能发电装置的水动力特性分析

3.1 波浪参数

改变规则波参数探究波能装置的功率变化特性，具体的仿真参数:浮子直径D=11 m,浮子吃水H=1.63 m，波浪周期Twave为4～10s，波浪高度Hwave为0.5～3.5 m，PTO阻尼系数CPTO为800,1 200 kN·s/m,PTO刚度系数KPTO=20 kN/m.图4为波能装置发电功率随波浪参数的变化.图5为波浪参数对波能装置发电功率的影响云图.

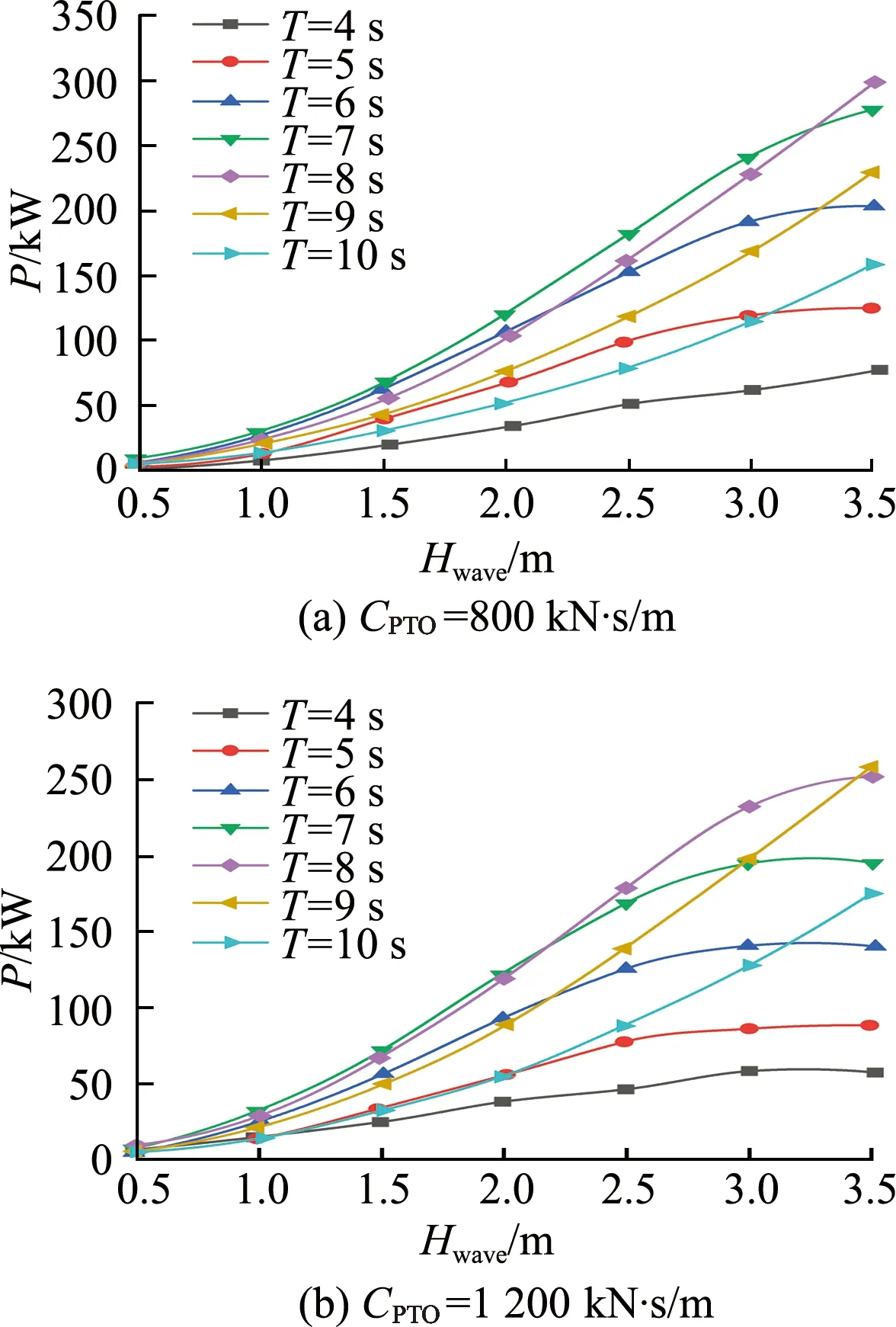
图4 波能装置发电功率随波浪参数的变化Fig.4 Influence of wave height on power generation of wave energy converter

从图4,5可以看出：① 波高一定的情况下，当波浪的周期大于8 s时，发电功率出现明显减小；② 发电功率随波高增加而增加，但当波高大于浮子水上高度时，会影响波能装置的功率变化；③ 对比不同PTO阻尼系数，对发电功率影响较小，均在8 s左右达到最大值.图6为波浪参数对波能装置的影响.

图5 波浪参数对波能装置发电功率的影响云图Fig.5 Influence contours of wave parameters on power generation

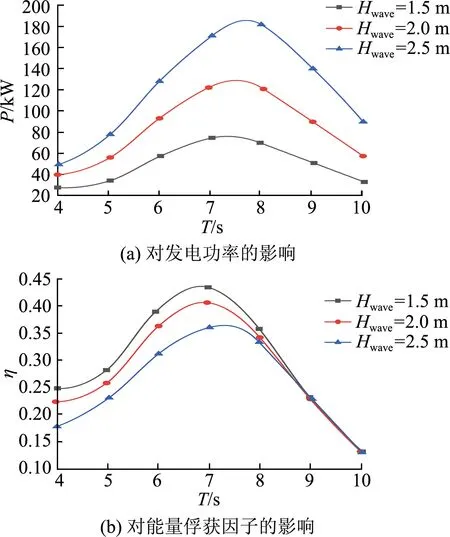
图6 波浪参数对波能装置的影响Fig.6 Influence of wave parameters on wave energy converter

从图6可以看出：① 发电功率P和能量俘获因子η均随波浪周期先增大后减小，存在1个最优波浪周期能使得发电效率最高；② 在最优周期之前，能量俘获因子η随波高增加而增加，随着周期的继续增大，波高对于能量俘获因子的影响较小.

3.2 发电装置尺寸参数

探究双浮体波能装置的尺寸对发电功率的影响，改变浮子直径、浮子吃水和浮筒阻尼板直径来探究发电功率的变化规律.

3.2.1 浮子直径

研究不同波浪周期下，波能装置发电功率随浮子直径的变化特性，具体参数D为9～13 m，H=1.63 m,Twave为4～9 s,Hwave=2.5 m,CPTO=1 200 kN·s/m,KPTO=20 kN/m.图7为浮子直径对波能装置的影响.

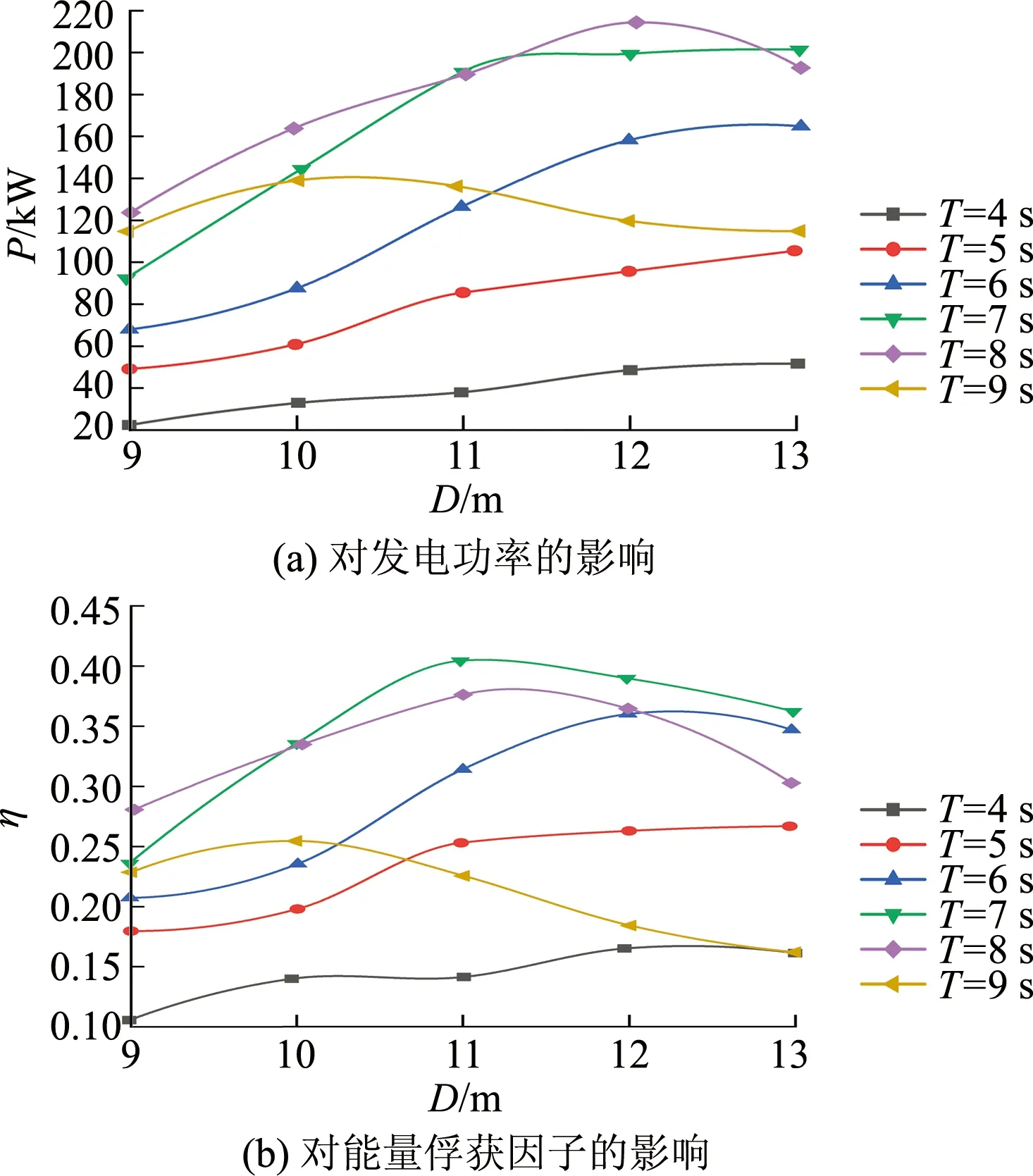
图7 浮子直径对波能装置的影响Fig.7 Influence of upper buoy diameter on wave energy converter

从图7可以看出：① 发电功率P和能量俘获因子η随浮子直径增大呈现相同的变化规律；② 浮子直径一定，发电功率随波浪周期增大，呈现“先增加后减小”趋势，且在周期为8 s左右达到最大；③ 周期一定，发电功率随浮子直径增大，呈现“先增长后减小或保持不变”的趋势，存在最优浮子直径，建议取12 m左右.

3.2.2 浮子吃水

改变浮子吃水，具体的参数:D=11 m；H为1.23,1.43,1.53,1.63,1.73,1.83 m;Twave为4～9 s;Hwave=2.5 m;CPTO=1 200 kN·s/m;KPTO=20 kN/m.图8为浮子吃水对波能装置的影响.

从图8可以看出：① 吃水一定时，发电功率P和能量俘获因子η在波浪周期为8 s时达到最值；② 周期一定时，当浮子的吃水小于1.63 m，发电功率和能量俘获因子随吃水增加而增加.而当浮子的吃水大于1.63 m时，改变浮子吃水，对发电功率和能量俘获因子的影响不大或呈负相关；③ 兼顾浮子稳性的前提下，建议选取吃水为1.63 m左右为最佳.

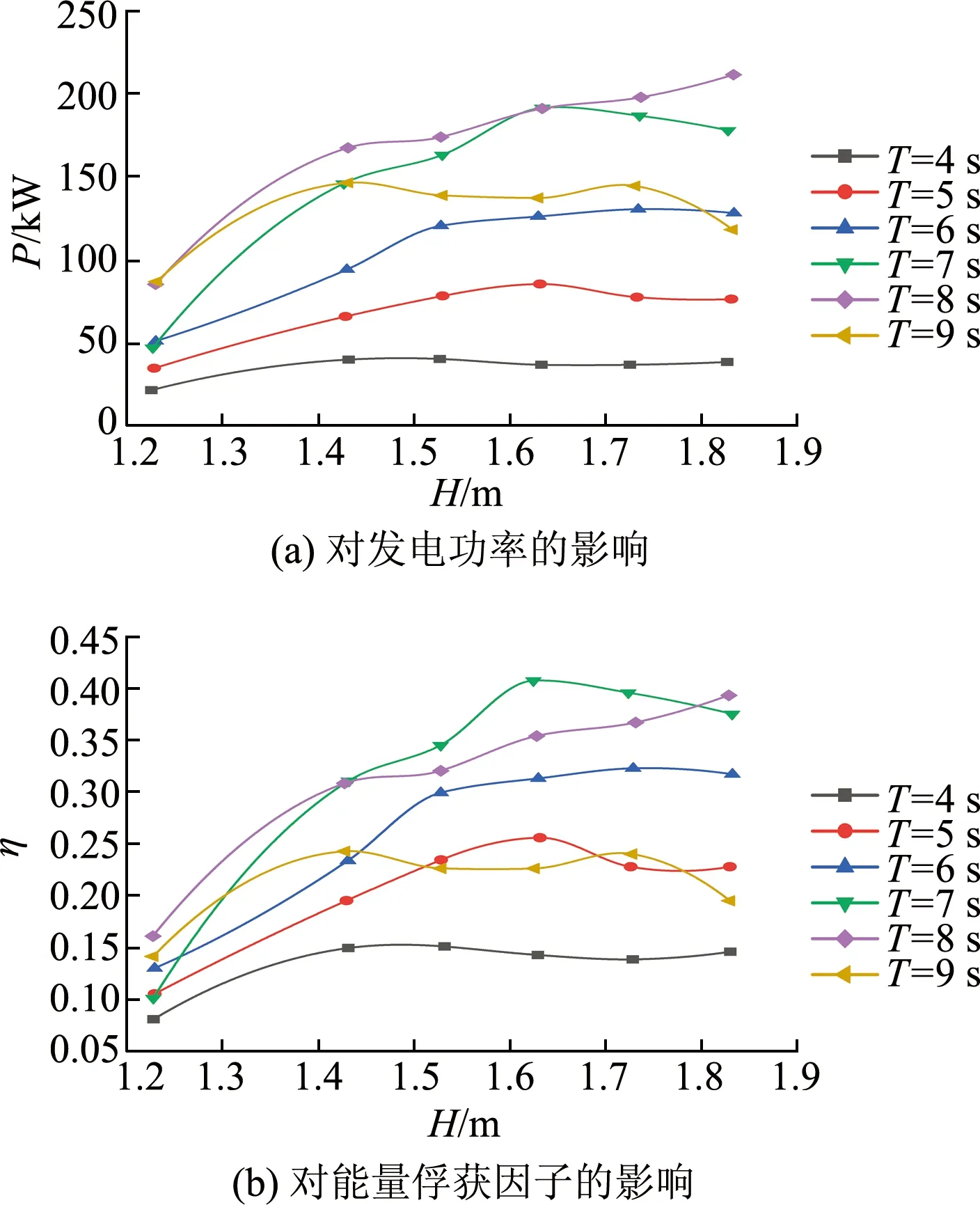
图8 浮子吃水对波能装置的影响Fig.8 Influence of upper buoy draught on wave energy converter

3.2.3 浮筒阻尼板直径

研究不同波浪周期下，浮筒阻尼板直径对波能装置发电功率的影响，具体的参数:阻尼板直径Dplate为12,13,14,15,16 m;D=11 m;H=1.63 m;Twave为4～9 s;Hwave=2.5 m;CPTO=1 200 kN·s/m;KPTO=20 kN/m.图9为浮筒阻尼板对波能装置的影响.

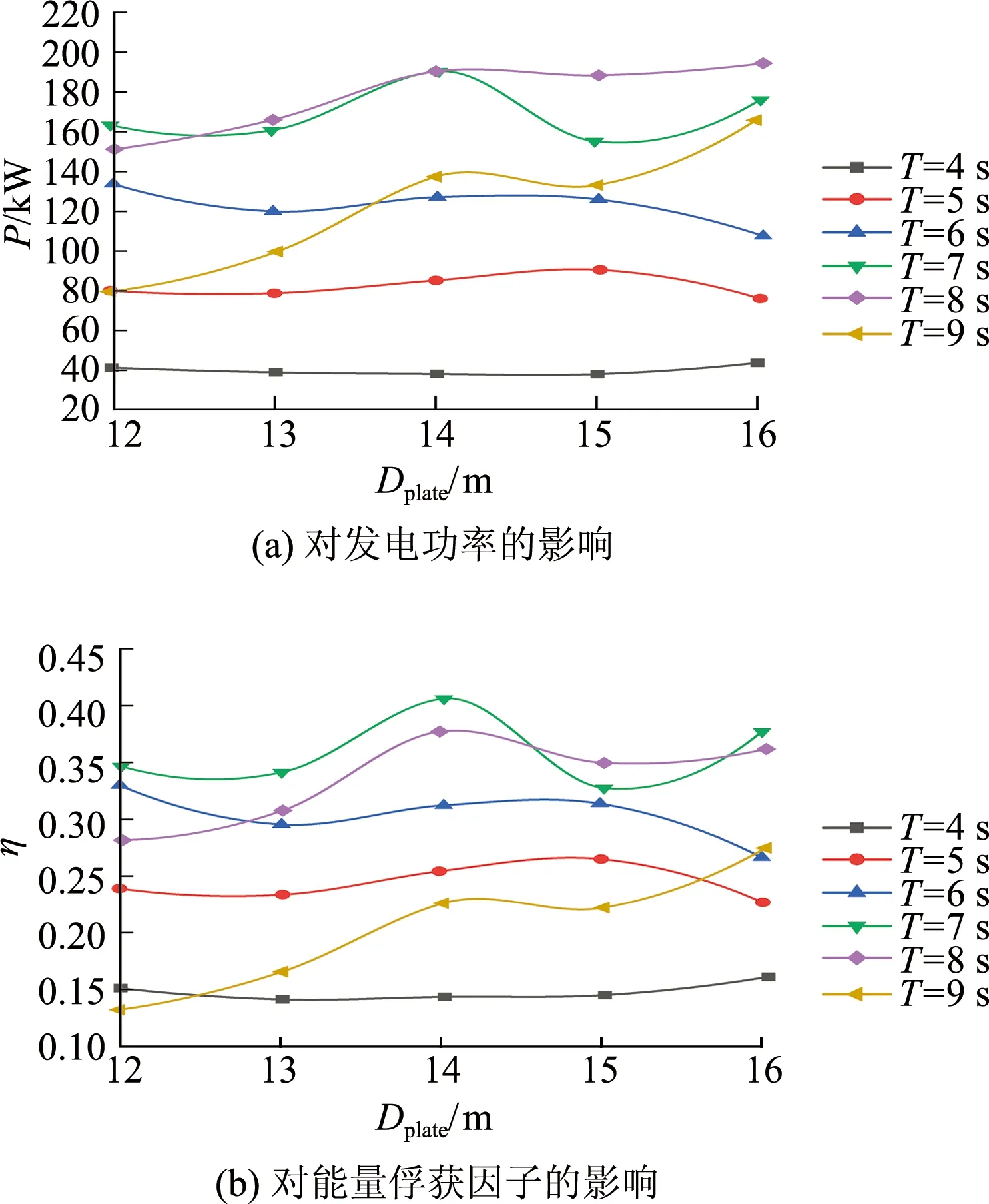
图9 浮筒阻尼板对波能装置的影响Fig.9 Influence of lower buoy damping plate on wave energy converter

从图9分析可得：① 当波浪周期为4 s时，发电功率和能量俘获因子基本不随阻尼板直径变化；② 周期大于4 s时，发电功率和能量俘获因子随阻尼板的直径总体呈现“先增大后减小”的趋势，综合兼顾成本等因素，建议阻尼板直径取14 m左右最佳.

3.3 PTO参数

考虑能量的线性转换，改变PTO装置阻尼系数和刚度系数，分析PTO参数对于波能装置发电功率的影响，具体的参数:Dplate=14 m;D=11 m;H=1.63 m;Twave=8 s;Hwave=2.5 m;CPTO为200,400,800,1 200,1 600,2 000,2 400 kN·s/m;KPTO为0,50,100,150,200,250,300 kN/m.

3.3.1 阻尼系数

图10为阻系系数对波能装置的影响.

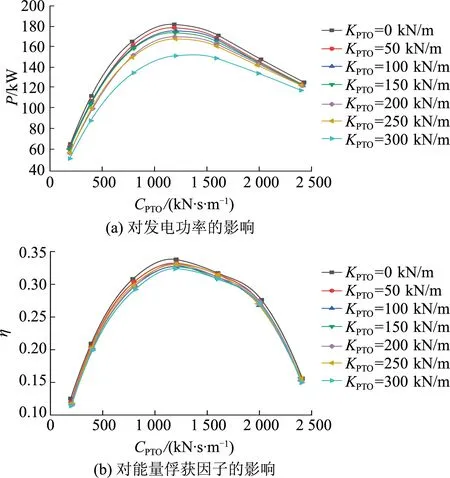
图10 阻尼系数对波能装置的影响Fig.10 Influence of damping coefficient on wave energy converter

图10表明随着PTO阻尼系数的增大，发电功率和能量俘获因子呈现“先增大后减小”的趋势，说明阻尼系数的增大，在一定范围内有利于提升波能装置的发电功率，但过大的阻尼又会限制双浮体装置的运动，从而导致功率减小，形成单峰.

3.3.2 刚度系数

图11为刚度系数对波能装置的影响.从图可以看出：① 发电功率随着PTO刚度系数的增大而逐渐减小或保持平稳；② 刚度系数超过250 kN/s时，发电功率明显减小.

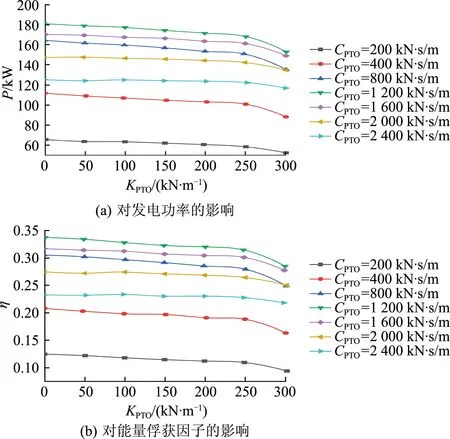
图11 刚度系数对波能装置的影响Fig.11 Influence of stiffness coefficient on wave energy converter

3.3.3 最优阻尼系数和刚度系数

为同时考虑阻尼系数和刚度系数对发电功率的影响，图12为不同阻尼系数和刚度系数对平均发电功率的影响云图.表2汇总了不同阻尼系数和刚度系数下的发电功率.分析可得：对于特定波浪参数下，以平均发电功率为最优指标，考虑工程实际情况，建议阻尼系数取1 200 kN·s/m左右，刚度系数取30 kN/m左右.

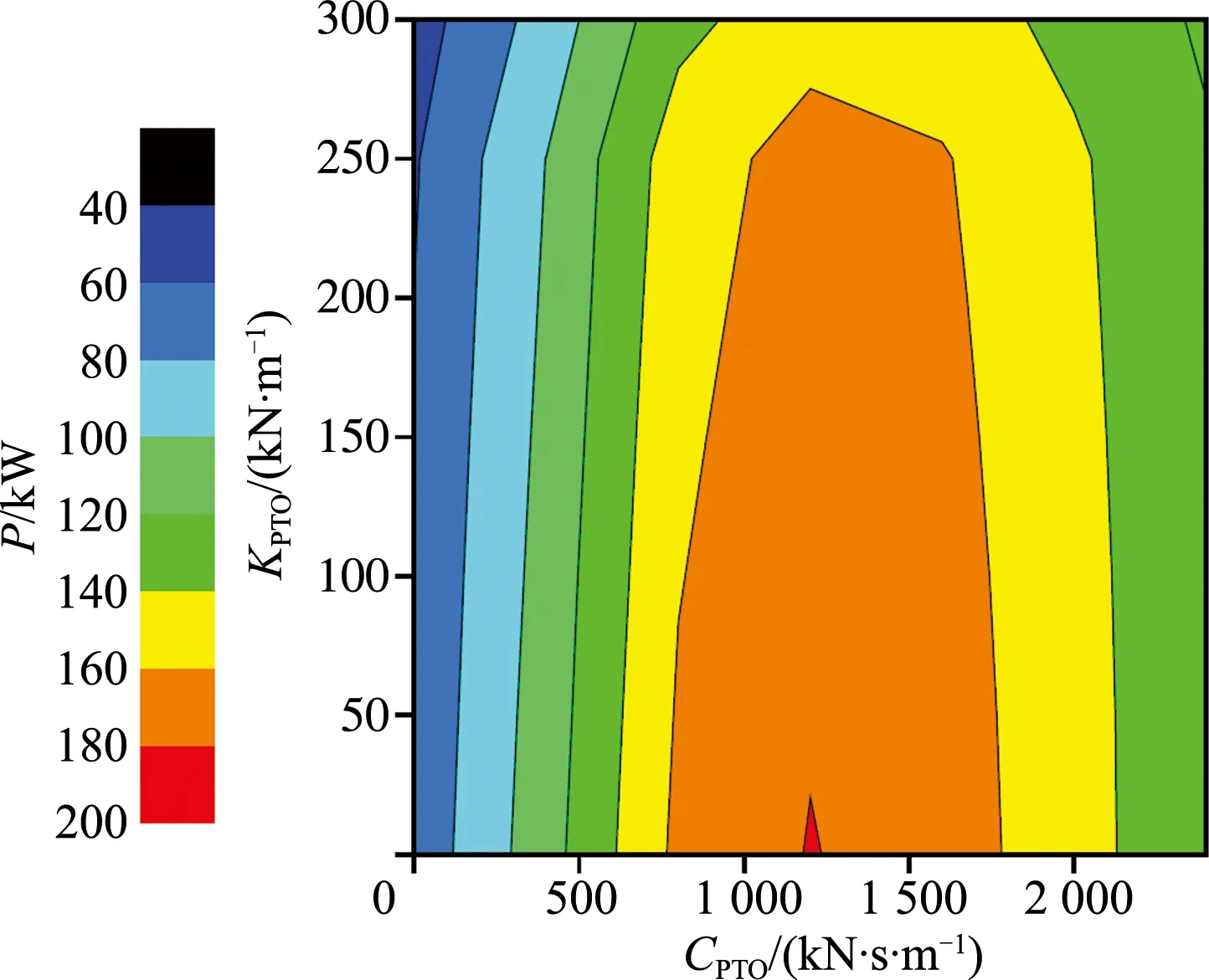
图12 阻尼系数和刚度系数对平均功率的影响云图Fig.12 Influence contours of damping coefficient and stiffness coefficient on average power

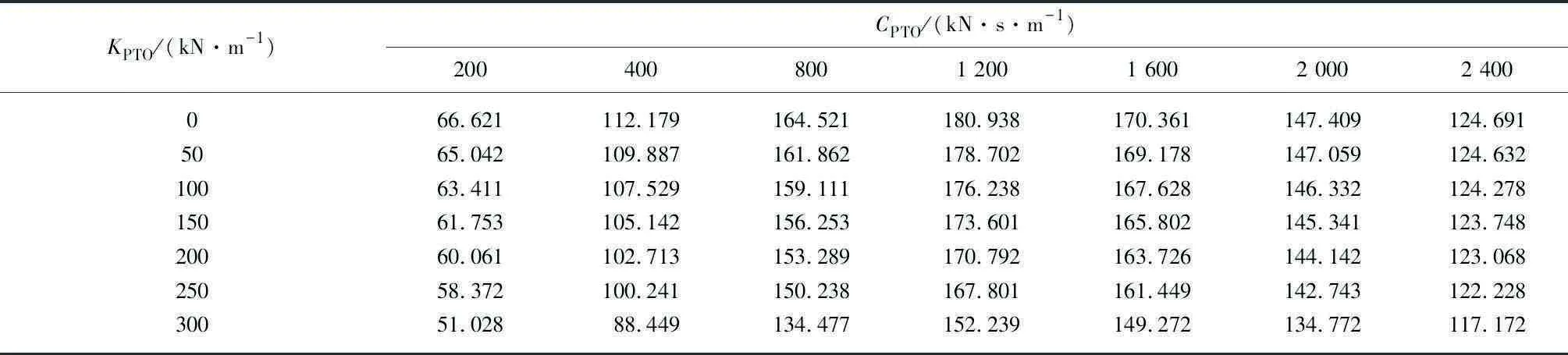
表2 不同阻尼系数和刚度系数下的平均功率Tab.2 Average power at different damping and stiffness coefficient

4 结 论

文中首先介绍了双浮体波能装置的基本理论，其次通过Fortran语言二次开发，引入PTO阻尼的影响，提出了基于ANSYS-AQWA研究振荡浮子式双浮体波能装置的时域计算方法，并将计算结果与NREL的试验进行对比，证明了此方法的可行性.最后深入探究了波浪参数、发电装置尺寸参数、PTO参数对波能装置发电功率的影响，研究结果表明：

1) 不同PTO阻尼系数对应不同的共振周期和最优吸收功率.

2) 在波浪参数方面，波高一定时，存在1个最优波浪周期，使得波能装置的发电功率最大；周期一定时，增加波高有利于波能的俘获.

3) 在发电装置参数方面，浮子吃水、浮子直径和浮筒阻尼板直径均存在最优值，使得发电功率和能量俘获因子达到最大，且文中给出了建议参考值.

4) 在PTO参数方面，波能装置的发电功率随阻尼系数的增大呈现“先增大后减小”的趋势，存在最优阻尼系数；阻尼系数一定时，发电功率随刚度系数的增大逐渐减小，但在一定刚度系数范围内变化较小.文中给出了工程实际中的相对参考值.