深海扬矿泵磨损特性的两相流数值模拟预测

刘少军,文豪,邹伟生,胡小舟*,董喆

(1.中南大学机电工程学院，湖南 长沙 410083；2.深圳市远东海洋矿产资源开发研究院有限公司，广东 深圳 518000；3.湖南大学流体力学及其装备研究所，湖南 长沙 410082)

近年来，在太平洋和印度洋的深海盆地中发现了大量稀土资源.稀土作为战略性资源吸引了世界各国的目光，将大大加快深海矿产资源商业化开采的步伐.中国的深海输矿系统是由软管、硬管和扬矿电泵组成的串联系统.作为深海采矿输送系统的核心部件之一，扬矿电泵的寿命直接决定着整个输矿系统的寿命，其性能也影响到整个输矿系统的性能.渣浆泵广泛应用在水利、电力、煤炭、冶金、石油化工等行业，而磨损问题严重影响其使用寿命与效率[1-2].深海扬矿泵用于输送被破碎的矿石颗粒以及海水的混合液体，也属于渣浆泵.传统渣浆泵一般采用离心蜗壳式泵，而深海扬矿泵采用叶轮导叶式泵，但目前对该泵型的磨损分析和研究甚少，所以本研究对深海扬矿泵的抗磨损设计及操作具有重要意义.

刘娟等[3]采用Euler-Lagrange两相流模型以及Finnie磨损模型，对离心泵内的过流部件的磨损特性进行研究，发现叶轮转速越大，颗粒在流道中的运动时间越短，与部件壁面发生撞击的概率也越小，且数值模拟与试验结果相吻合.吴波等[4]应用雷诺涡黏模型(液相)和离散相流动模型(固相)研究渣浆泵内固相颗粒的冲蚀特性，发现随着转速的提高，颗粒的冲击速度和冲击角度增大，因此渣浆泵应避免在过高的转速下运行.MEHTA等[5]使用PIV技术研究不同颗粒体积分数和转速下渣浆泵内的颗粒行为，表明渣浆泵转速越快，泵内颗粒的运动速度越快.基于Finnie磨损模型，SONG等[6]分析了射流泵内过流件的磨损情况.ZHONG等[7]利用Euler-Lagrange方法和Bitter磨损模型研究砂砾对泵蜗壳的磨损，发现颗粒直径越大，磨损越严重.PAGALTHIVARTHI等[8]通过DPM模型分析渣浆泵的运行参数、流量、转速、颗粒粒径以及泵几何形状对其磨损的影响，发现随着流量的增大，磨损曲线变得更为平缓.杨凌波等[9]采用Euler-Lagrange两相流模型和Finnie磨损模型分析纸浆泵的磨损特性，模拟结果与实际情况一致.

文中基于Euler-Lagrange两相流模型以及Finnie磨损模型，探讨深海扬矿泵在不同流量、转速以及输送不同固相体积分数时的磨损特性.利用离心泵送试验系统以及中国“十一五”期间制造的1台2级提升电泵进行模型验证，对未来深海扬矿泵的抗磨损设计提出相关建议.

1 数学模型

1.1 固液两相流模型

文中的固相体积分数φ均小于12%，故选用Euler-Lagrange两相流模型，将颗粒视为离散相、流体介质(水)为连续相，在CFX软件中将矿物颗粒设置成Particle Solid(固体颗粒)、结核密度2 000 kg/m3，颗粒与流体的作用方式为双向耦合，运动模型采用Particle Transport Solid(固体颗粒输送模型).对于颗粒有如下假设：① 密度恒定；② 颗粒为质点，不占空间体积，并忽略其相互作用；③ 每个颗粒不是实际运动的颗粒，而是颗粒样本，因此无邻壁效应或涡流等流体现象；④ 每相的颗粒质量流量平均分配到每个颗粒上；⑤ 颗粒为不发生形变的刚体.基于以上假设，颗粒的动量方程为

mP(-2Ω×UP-Ω×Ω×rP)+

(1)

式中：mP为固体颗粒的质量；UP为固体颗粒在旋转坐标下的相对速度或静止坐标系下的绝对速度；UF为液体颗粒在旋转坐标下的相对速度或静止坐标系下的绝对速度；CD为固体颗粒的阻力系数，CD=0.44;ρF为流体的密度；AF为颗粒的有效断面面积；rP为颗粒运动的转动半径；Ω为泵的选择角速度；p为压力梯度；FD为阻力；FB为浮力；FR为离心力与科氏加速度力；FVM为虚拟质量力；Fp为压力梯度力;CVM为虚拟质量力的影响因素.

液相选用考虑旋转效应的RNGk-ε湍流模型，其湍流耗散公式为

(2)

1.2 磨损模型

与其他磨损模型相比，Finnie磨损模型对颗粒的处理方式更适合本研究，使用也更便利，故文中选用该模型预估磨损强度.改进的Finnie磨损模型[10]为

(3)

式中：E为被切削材料的体积磨损量；m为单个颗粒的质量；v为磨损颗粒的撞击速度；θ为撞击角度；ψ为切削长度与深度比；p1为材料塑性流动应力；K为冲击应力的垂直和水平分量比.

文中采用磨损速率ve衡量磨损程度，与磨损程度成正比.ve的计算公式为

ve=E·N·mP，

(4)

式中：N为每秒撞击壁面的颗粒数量.

1.3 流体域建模

文中使用的深海扬矿电泵模型是中国“十一五”期间研制的2级提升电泵，其主要设计参数如下：当流量Q=420 m3/h、转速n=1 450 r/min时，单级扬程H=40 m；可通过的最大粒径dm=50 mm、最大体积分数φm=10.00%.表1为电泵模型的主要几何参数，表中，k为叶轮叶片数；D1，D2分别为叶轮入口、出口直径；B为出入口宽度；β1，β2分别为叶轮入口、出口安放角；ψ1，ψ2分别为叶轮、导叶包角；α1，α2分别为导叶入口、出口安放角.图1为泵内各过流部件命名示意图.

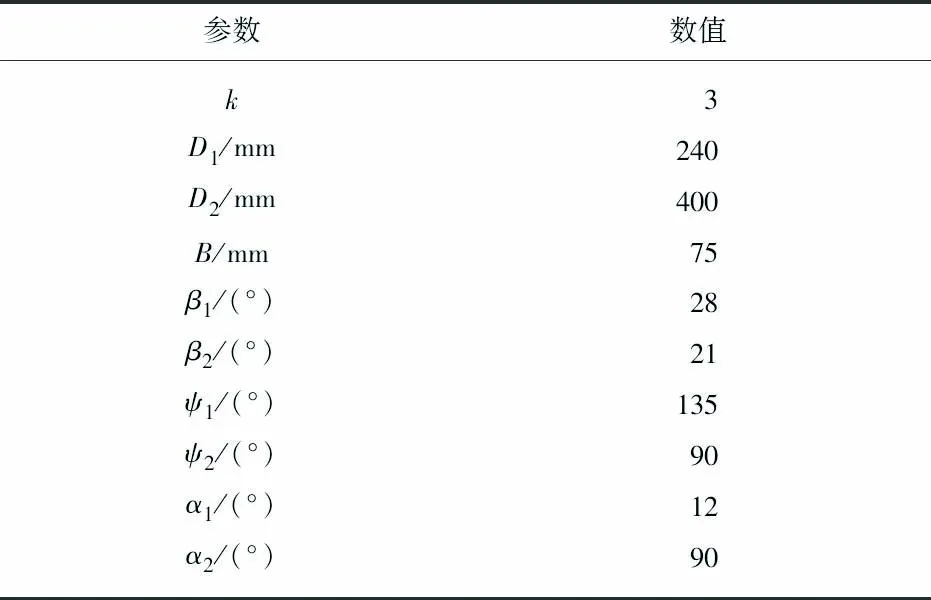
表1 模型主要几何参数Tab.1 Main geometric parameters of the model

图1 泵内各过流部件命名示意图Fig.1 Schematic diagram of hydraulic component names in pump

利用专业旋转机械造型软件BladeGen对叶轮和导叶造型，使用旋转机械网格划分工具Turbogrid进行全六面体结构网格划分，如图2所示，其中叶轮网格数1 537 920、导叶网格数1 932 000.将叶轮和导叶的网格导入CFX软件进行旋转复制组装.

图2 2级泵网格图Fig.2 Mesh of pump

1.4 边界条件设定

仿真采用开放式压力入口、入口静压101 325 Pa；固体颗粒的入射速度为无滑移入射，即在入口处液相和颗粒相的速度一致且入射位置随机，粒径d的配比与文献[11]中一致，如图3[12]所示，图中ω为质量分数,采用集矿机破碎后的结核粒径组成；采用质量流量出口；叶片、轮毂以及泵体边界均为无滑移边界，壁面粗糙度0.02 mm；叶轮域与导叶域采用普通连接(general connection)中的网格连接，连接方式为普通网格界面(general grid interface，GGI).

图3 颗粒粒径组成Fig.3 Particle size composition

2 试验验证

为了验证仿真的准确性，将仿真数据与文献[11]提供的中国“十一五”期间研制的2级电泵试验数据进行对比，如图4所示，图中H为扬程，P为功率，Q为流量.由图4可知，CFD仿真扬程存在一定的波动，这主要是由于颗粒入射位置与颗粒粒径分布均存在随机性，但仿真扬程的最大相对误差为8.9%，这对固液两相流计算是可以接受的.与试验数据相比，仿真扬程更高，可能是由于模拟颗粒并不完全是球体，输送过程中损失的能量更多；仿真的功率更低，可能是因为仿真计算中未充分考虑机械损失与容积水力损失.这说明本次仿真试验使用的计算模型能准确预测泵的性能，再根据文献[12]对相关研究的总结，可知其也能准确模拟泵内的固液两相流动.

图4 仿真与试验的性能曲线对比Fig.4 Comparison of numerical simulation and experimental hydraulic characteristic curves

3 结果分析

3.1 磨损与流量的关系

图5为当转速n=1 450 r/min、输送颗粒体积分数φ=5.14%时，泵在不同流量下过流部件的磨损速率.从图5可知，随着流量的增大，叶轮各过流部件的磨损速率增大，而导叶磨损速率的变化并不明显.

图5 泵的过流部件在不同流量下的磨损速率Fig.5 Wear rate of pump hydraulic components at different flow rates

随着流量的增大，由于单位时间内通过叶轮的颗粒增多，因此叶轮各过流部件的磨损速率增大，而导叶内的轴向速度也增大.由文献[13]的研究可知，输送同一体积分数、同一粒径配比的渣浆时，随着流速的增大，颗粒相的滑移速度减小，跟随性也更好，所以颗粒相通过导叶内部的时间越短，其与导叶碰撞的概率越小，从而导叶的磨损速率随着流量变化的改变并不明显.加之深海扬矿泵采用空间导叶式的压水室，不同于蜗壳式的压水室.随着流量的增大，蜗壳式压水室的颗粒相在出口处的径向速度增大，颗粒与蜗壳的碰撞概率和碰撞速度也增大，所以其蜗壳磨损速率增大；但导叶式渣浆泵的导叶磨损速率随着流量变化的改变并不明显.图6为泵内流场颗粒轨迹分布，图中v为颗粒运动速度.从图6中可知，随着流量的增大，颗粒的轴面速度增大，其在叶轮出口处速度角增大，颗粒与导叶叶片的碰撞点也从导叶头部向尾部移动，且颗粒与导叶叶片背面的碰撞次数增多.

由于受到重力与离心力的作用，颗粒与叶轮上盖板以及叶片的碰撞概率以及碰撞速度变得更大.由图5可知，颗粒粒径越大，受到的重力与科式力越大.由5b可知，随着流量的增大，颗粒入射时的轴向速度变大，其与叶轮下盖板碰撞的概率也变大.如图6，7所示，叶轮叶片的压力面受磨损比较严重，应加强保护.

图6 泵内流场颗粒轨迹分布Fig.6 Particle trajectory distribution of pump flow field

图7Q=600 m3/h时叶轮的吸力面与压力面的磨损速率对比
Fig.7 Comparison of wear rate on blade pressure surface and suction surface at a flow rate of 600 m3/h

3.2 磨损与转速的关系

图8为当流量Q=432 m3/h，φ=5.14%时，泵各过流部件在不同转速下的磨损速率.从图8可知，叶轮和导叶的各过流部件磨损速率均随着泵转速的增大而增大.这是由于随着泵转速的增大，颗粒在叶轮内受到的牵连加速度更大，颗粒与过流部件的碰撞速度和碰撞概率更大，从而导致磨损速率增大，如图9所示.导叶的作用主要是将液体的速度能转换为压力能，而液体与颗粒通过导叶时轴面速度变化不大，牵连速度从叶轮出口到导叶出口逐渐减小(由最大降至约为0)；转速越大、颗粒在叶轮出口处的牵连速度越大，其与导叶过流部件的碰撞速度就越大，从而转速越大，因此导叶各过流部件的磨损速率也越大.转速越大，颗粒所受的离心力越大，其与叶轮上盖板的撞击速度更大，并且会有更多颗粒撞击叶轮上盖板，致使其磨损更严重.从图9中可知，叶轮叶片的压力面和导叶叶片的正面仍是磨损严重的部位.

3.3 磨损与颗粒浓度的关系

图10为当Q=432 m3/h，n=1 450 r/min时，泵内各过流部件输送不同固相体积分数颗粒的磨损速率.从图10可知，随着固相体积分数的增大，泵内各过流部件的磨损速率也增大.这是因为随着体积分数的增大，单位时间内通过泵内的颗粒增多，颗粒与泵过流部件的碰撞更频繁，导致过流部件的磨损速率更大.

图8 泵各过流部件在不同转速下的磨损速率Fig.8 Wear rate of pump hydraulic components at different rotating speeds

图9 泵内流场颗粒轨迹分布图Fig.9 Particle trajectory distribution of pump flow field

图10 泵各过流部件输送不同固相体积分数颗粒时的磨损速率Fig.10 Wear rate of pump hydraulic components when transmitting particles with different volume fractions

4 结 论

1) 随着流量的增大，叶轮过流部件的磨损速率明显增大，但导叶过流部件的磨损速率变化并不明显.这不同于蜗壳式渣浆泵,原因可能是随着流量的增大，颗粒的随流性更好，与导叶的碰撞概率减小，并且颗粒的轴向速度增大，通过导叶的时间更短，与导叶碰撞的次数减少.

2) 随着转速或颗粒体积分数的增大，叶轮与导叶过流部件的磨损速率均明显增大.如果希望减少磨损，可以降低转速或输送颗粒的体积分数.

3) 根据等寿命设计原则，叶轮过流部件应选用比导叶过流部件更耐磨损的材料.

4) 叶轮叶片的压力面与导叶叶片的正面是磨损严重部位，应加强这2个部位的抗磨损性能.