岩石分数阶蠕变损伤本构模型研究
2020-06-22张向东周林林
苏 彦,张向东,周林林
(1. 天津华铁工程咨询有限公司,天津 300202;2. 辽宁工程技术大学 土木工程学院,辽宁 阜新 123000)
随着我国西部地区基建设施的不断完善,岩石的蠕变力学性能得到了学者广泛关注。在原岩应力状态下,岩体随着时间发展其变形不断累积,蠕变分衰减、稳定和加速蠕变阶段,衰减蠕变阶段是蠕变过程的开端,稳定蠕变阶段是长期保持的过程,当岩体应力状态达到屈服条件时,稳定蠕变阶段结束,进入加速蠕变阶段,岩体破坏。边坡工程、水利水电工程、采矿工程等工程实践中的灾害发生常与岩体蠕变有关。
岩石蠕变模型是描述应力、应变及时间之间关系的状态方程,研究岩石蠕变模型对于岩石蠕变发展过程的认识与控制具有重要作用。关于岩石蠕变模型的研究,目前已有大量成果,蒋春祥等[1]以深部岩石为研究对象,在传统西原模型的基础上,将黏塑性扩展为n个,建立一种新的广义模型;张树光等[2]通过引入过应力差和时间乘积的概念,构建考虑时效性和应力状态的损伤模型;周倩瑶等[3]引用了裂隙压密体元件,对岩石蠕变过程中的瞬时塑性变形进行描述,将该元件与Poyting-Thomson模型进行串联得到可较好描述岩石蠕变裂隙压密的本构模型;周宏伟、王春萍等[4-5]以盐岩为研究对象,构建了一种新的流变元件分数阶Abel粘壶,将其代替经典西原模型中Newton黏壶,从而得到新的分数阶导数模型。
为了描述岩石在不同应力状态下的蠕变变形全过程,本文基于损伤力学理论对Young模量进行改进,基于分数阶微积分反映黏弹性应变和黏塑性应变,并引入SN元件对描述黏弹性应变的软体元件进行改进,最终得到一个非线性的岩石分数阶蠕变损伤本构模型。相比传统参数定常的线性蠕变本构模型,本文模型为具备非线性特征的参数非定常蠕变模型,能从某种意义上表征岩石蠕变的损伤发展过程。
1 岩石蠕变损伤分析
1.1 损伤变量定义
根据损伤力学理论,损伤变量的定义主要有两种方法:(1)几何损伤中通过结构有效承载面积定义;(2)能量损伤中依据Young模量变化定义。由于几何损伤难以测定,故本文采用第二种方法定义损伤变量。
大量试验发现,蠕变过程中岩石的Young模量和黏滞系数通常随时间的增长而减小[6],文献[4]进行软岩单轴压缩蠕变试验,得到蠕变过程中不同时刻的Young模量,如表1和图1所示。
依据图1通过能量损伤的方法进行损伤变量定义,首先作如下定义:(1)当t=0时,损伤变量D=0;(2)当t→∞时,损伤变量D=1;(3)随着时间的逐渐增长,损伤变量D逐渐趋于1。
由此建立如下损伤演化方程:
D(t)=1-e-bt
(1)
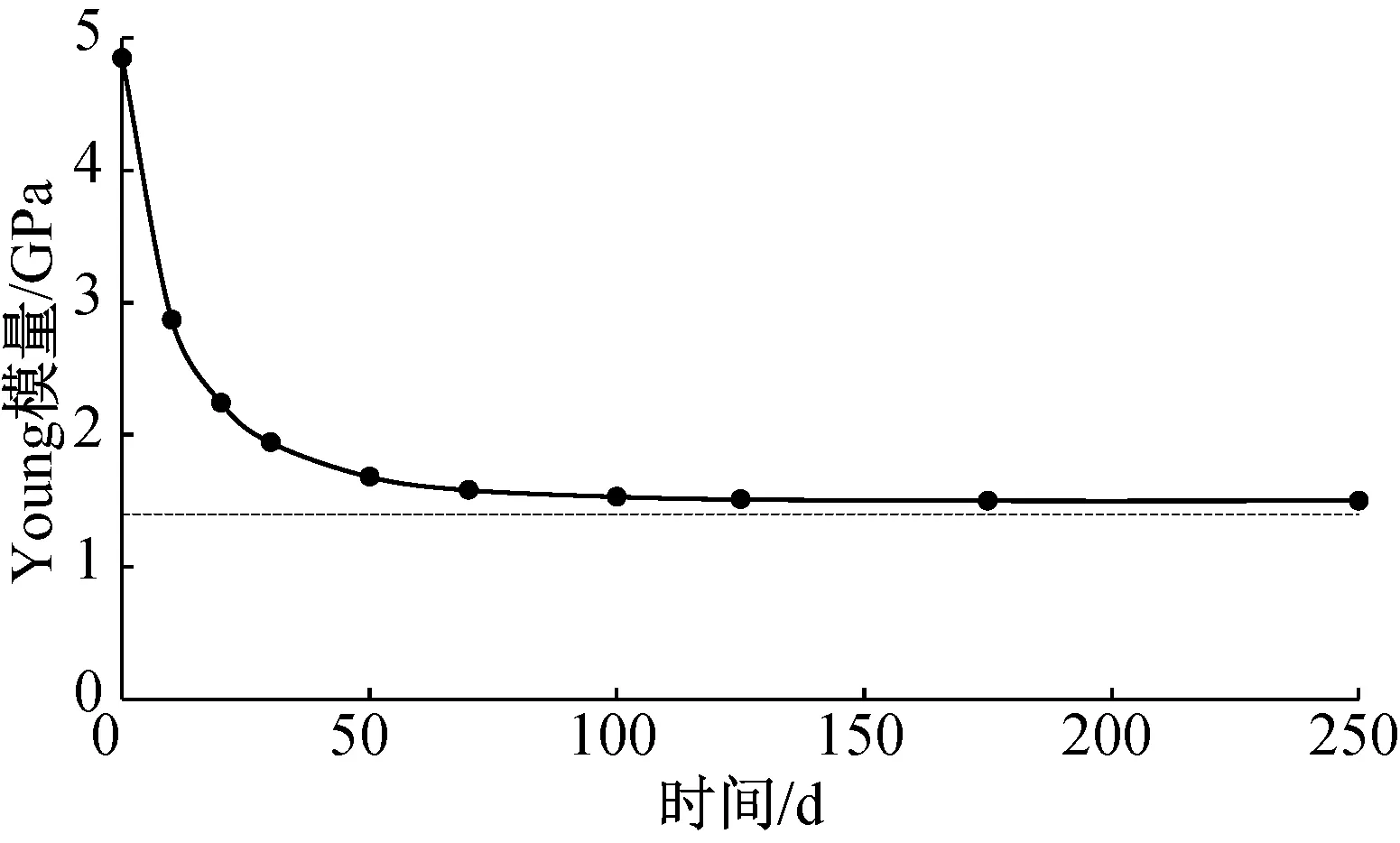
图1 Young模量衰减曲线Fig.1 Decay curve of Young modulus
式中:b为与材料损伤程度相关的参数。
1.2 考虑损伤的弹性体
假设岩石材料为各向同性损伤,则Young模量的损伤过程可表示为
E(t)=E0[1-D(t)]
(2)
式中:E0为初始Young模量。
当应力超过屈服应力时,此时损伤急剧累积,岩石进入加速蠕变阶段。无损状态的岩石,用Hooke体描述其弹性应变
(3)
式中:εe为弹性应变,σ为初始应力。
当应力超过屈服应力时,通过Lemitre应变等效原理可得
(4)
式(4)即为考虑损伤的弹性体的状态方程。取E0=4.85 GPa,b=0.05,可得表1和图1试验值的拟合曲线,如图2所示。
2 分数阶黏滞体和黏塑性体
2.1 Riemann-Liouville型分数阶微积分
分数阶微积分在非线性动力系统中应用广泛,在解决非线性非局部问题中具有独到的优势[7]。
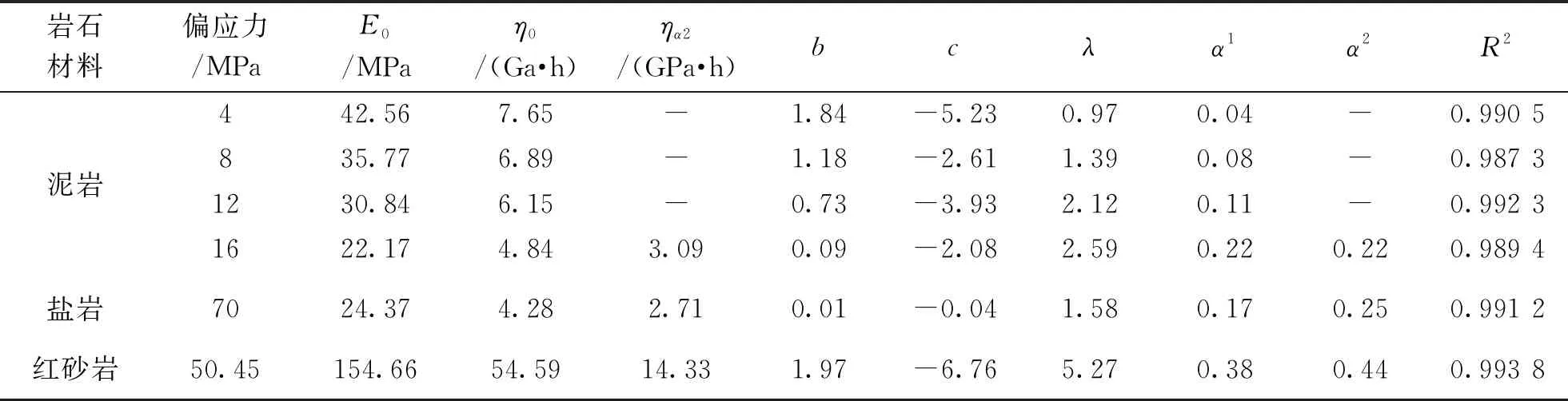
表1 蠕变损伤本构模型参数

图2 Young模量拟合曲线Fig.2 Fitting curve of Young modulus
本文引入Riemann-Liouville型微积分,函数f(t)在可积区间[0,t]的α阶Riemann-Liouville积分定义为
(5)
式中:t为时间,f(t)为在可积区间[0,t]的某一函数,Γ(α)为伽马函数,a为大于0的分数阶数,S为用于拉普拉斯变换的某一自变量。
相应地,函数f(t)的α阶微分定义为
(6)
式(5)—(6)中,α>0,n=[α],Γ(α)为Gamma函数,其定义为
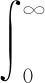
(7)
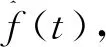
(8)
2.2 基于分数阶微积分的软体元件
岩石是一种非均质非线性的地质材料,被认为介于理想固体和理想流体之间,引入描述该状态的软体元件[5],如图3。
图3 软体元件Fig.3 Software component
该软体元件的状态方程为
(9)
式中:σ为应力,εve为应变,t为时间,ηα为该软体元件中的黏滞系数。
在同一级荷载作用下,通过Riemann-Liouville分数阶微积分算子理论,对式(9)进行分数阶积分得
(10)
式(10)即为基于分数阶微积分的软体元件。
2.3 基于分数阶微积分的变参数黏滞体
由于式(10)中黏滞系数是一个定值,ηα在某一层面上可反映岩石衰减、稳定蠕变阶段的蠕变应变累积,而实际岩石蠕变长期发展过程是一个非线性变化过程,用一个定值定义黏滞系数存在不合理的地方,文献[8]提出一种与时间和应力有关的SN元件,该元件的状态方程为
(11)
式中:η0,λ,c为与蠕变特性相关的黏滞参数。
将式(11)代入式(10)即可得改进后的分数阶变参数黏滞体,其状态方程为
(12)
2.4 分数阶黏塑性体
当应力超过屈服应力σp时,岩石材料进入加速蠕变阶段,此时产生黏塑性应变。利用黏塑性体来描述黏塑性应变εvp。该黏塑性体的总应力可表示为
σ=σu+σv
(13)
式中:σv代表黏滞体中的应力,σu定义为
(14)
当σ≥σp时,黏塑性体中的总应力为:
(15)
式中:ηα2为黏塑性体中的黏滞系数。
利用Riemann-Liouville型分数阶微积分,对式(15)进行积分可得
(16)
式(16)即为本文用于描述黏塑性应变的分数阶黏塑性体。
3 本构模型的建立及模型验证分析
3.1 本构模型的建立
将考虑时效损伤的弹性体、分数阶变参数黏滞体和黏塑性体串联,建立一个基于分数阶微积分的岩石蠕变损伤本构模型(图4)。
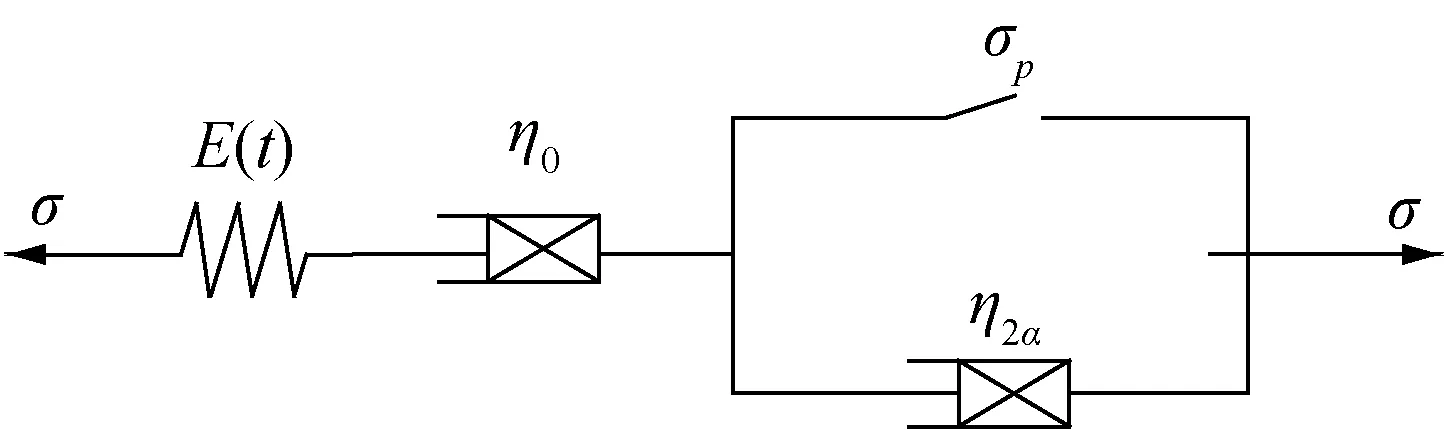
图4 蠕变损伤模型Fig.4 Creep damage model
根据图4中模型结构特点,结合式(3)、(4)、(12)和(16)可得本文蠕变本构方程
(17)
式(17)即为本文新建的分数阶蠕变损伤模型。
3.2 三轴压缩蠕变试验
本文采用RLW-2000三轴流变试验系统(图5),该系统由轴向加载系统、围压加载系统、孔压加载系统、伺服系统、控制系统、数据采集和自动绘图系统等部分组成。轴向加载系统和围压加载系统的控制部分采用全数字伺服控制器(EDC),设备最大加载围压70 MPa,最大轴向荷载2 000 kN。开展三轴压缩蠕变试验,试验对象为红层泥岩,侏罗系中统沙溪庙组地层,紫红色层状结构,取自四川某红层边坡滑带附近,该边坡具有显著的蠕滑现象。将试样加工成Φ50 mm×100 mm的圆柱样,根据滑带深度,将围压设置为2 MPa,常规三轴压缩试验测得三轴抗压强度为20.14 MPa,本文假定三轴抗压强度的80%为长期强度,故偏应力水平分别设为4、8、12和16 MPa。

图5 岩石三轴流变试验系统Fig.5 Triaxial rheological test system of rock
3.3 蠕变试验结果
由于三轴流变试验系统中的蠕变试验数据是逐级增量加载的形式,为了便于开展研究和模型验证,基于Boltzmann线性叠加原理[3]处理原始数据可得分别加载形式的曲线,如图6所示。
由图6可看出,前3级偏应力水平下,蠕变曲线较为相似,首先在加载瞬间变现出瞬时弹性应变,接着进入衰减蠕变阶段,该阶段历时较短,然后进入稳定蠕变阶段,应变量值的累积速度逐渐放缓。当达到破坏应力水平时,岩石表现出加速蠕变阶段,随即岩石屈服破坏。
3.4 模型验证
利用本文所建模型,通过数学分析软件1stOpt,基于BFGS算法和通用全局优化法对本文试验数据进行辨识,结果如图7所示,模型参数如表1所列。

图7 拟合对比图Fig.7 Fitting contrast chart
由图7可看出,本文所建模型拟合效果较好,平均R2为0.989 9,能较为准确地反映红层泥岩的三轴蠕变力学特性。为了验证本文模型的适用性,引用文献[9]中的盐岩和文献[10]中的红砂岩的蠕变试验数据,由于不同岩石材料的蠕变特性的差异主要体现在破坏偏应力水平的完整蠕变三阶段,故只引用盐岩和红砂岩最后一级加载的蠕变试验数据。图8为盐岩和红砂岩的拟合对比图,表2为相应的模型参数。
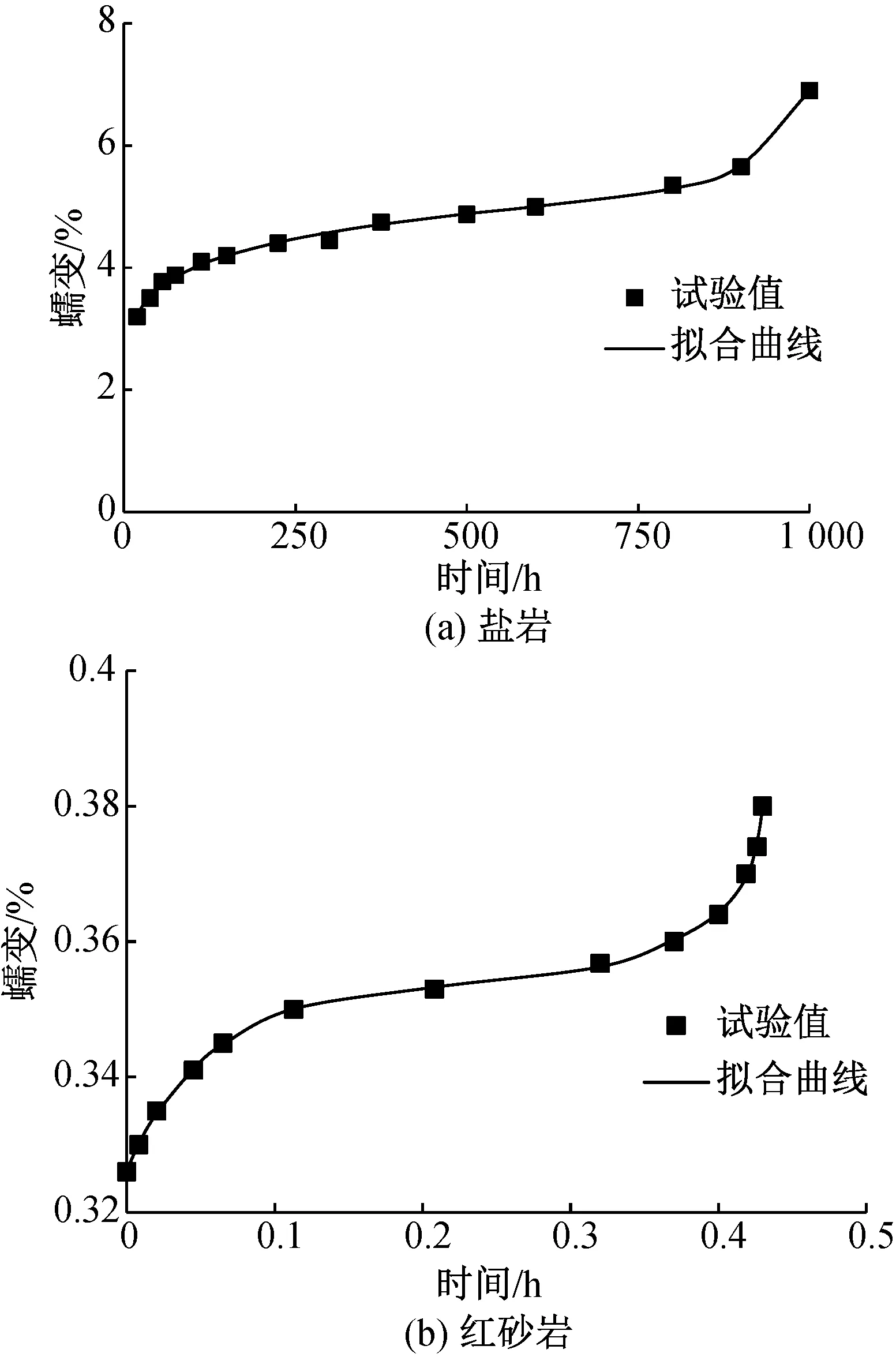
图8 拟合对比图Fig.8 Fitting contrast chart
综合图7、图8可看出,本文所建模型对岩石蠕变曲线的辨识能力较好,能描述不同曲线形态的加速蠕变阶段,克服常规元件模型难以表征加速蠕变阶段的困难,总体而言本文模型能较为准确地反映岩石的蠕变特性。
4 结论
1)本文基于损伤力学理论对Young模量进行改进,基于分数阶微积分反映黏弹性应变和黏塑性应变,并引入SN元件对描述黏弹性应变的软体元件进行改进,最终得到一个非线性的岩石分数阶蠕变损伤本构模型。
2)开展红层泥岩三轴压缩蠕变试验,并引用盐岩和红砂岩典型蠕变试验数据,利用BFGS算法和通用全局优化法识别蠕变试验曲线,求解模型参数,验证了模型的合理性和正确性。
3)本文所建模型对于不同形态的岩石蠕变曲线有较好的识别能力,克服传统蠕变本构模型难以较好辨识加速蠕变阶段的困难,所建模型可为工程实践中岩体长期稳定性研究提供一定参考。
