三面围合盾构隧道底板注浆对地下通道结构的影响

2020-06-22覃涛，冯云，郭健，杨潇，黄沛

河北工程大学学报(自然科学版) 2020年1期

覃涛，冯云，郭健，杨潇，黄沛

(1. 同济大学地下建筑与工程系，上海 200092；2. 上海市隧道工程轨道交通设计研究院，上海 200235；3. 武汉地铁集团有限公司，湖北武汉 430030；4. 长安大学土木工程学院，陕西西安 710061)

随着城市地下空间不断开发利用，盾构隧道的近接施工日益增多，近年来更是出现了隧道与地下通道平行叠置的工程。此时，盾构隧道处于地下通道底板和两侧围护墙体的三面围合中，隧道施工对周围环境的影响与半无限空间相比，有较大的差别。盾构隧道施工过程中，在掌子面后方，地下道路底板与下方土体接触松弛乃至脱空，引起地下道路结构的附加应力和变形。此时，对地下道路底板下方的空隙进行注浆，可以起到填充空隙加固土体的作用，以减少附加应力和变形。但是注浆过程会对底板产生一定的压力，当该压力达到一定程度时，可能引起底板结构局部变形过大乃至开裂。因此底板注浆对地下通道底板的影响规律及如何选取合适的注浆压力是急需研究的问题。

在盾构隧道注浆领域，已有很多学者从数值模拟[1]、理论推导[2-5]、现场数据分析[6-7]、实验[8]等方面进行研究，但是这些研究主要集中于半无限空间中的盾构隧道和盾尾注浆领域。关于隧道与地下通道上下叠置领域，杨潇[9]、李本[10]等学者已进行相关研究，但其主要从整体来研究盾构施工引起的相关力学行为，未关注与注浆相关的领域，对关于三面围合空间中地下通道底板注浆对结构的影响，鲜有学者进行相关的研究。因此，对地下道路底板注浆引起的地下道路结构和盾构隧道结构的变形进行计算研究是十分必要的。

1 注浆压力分布和地下通道结构内力计算

1.1 注浆压力计算的理论推导

本文借鉴叶飞等人[10-11]的研究方法对地下道路底板下方的注浆问题进行分析。假设注浆浆液在地下道路底板下方脱空影响区域沿与底板表面平行的方向四周均匀扩散，其中脱空影响区域的厚度也按照浆液注入率进行确定。

由于地下道路底板与下方土体接触松弛并局部脱空，造成一定范围内的土体孔隙率要大于土体原始孔隙率，则在浆液扩散厚度范围内的土体等效孔隙率为

(1)

式中，n为土体原始孔隙率，r为经过注浆时间t后浆液的扩散半径，d为底板脱空厚度，λj为浆液注入率。

根据达西定律，有注浆量

(2)

式中，Kg为浆液在扩散厚度范围内土体中的渗透系数，K为水在浆液扩散厚度范围内土体中的渗透系数，β为浆液黏度与水的黏度之比，A为浆液渗透过程中经过的任意圆柱面积，有A=2πrλjd，t为注浆时间。

假设注浆孔半径为r0，根据边界条件，在r0处，浆液压力为注浆压力pg，在r处，浆液压力为pr，则

(3)

考虑到注浆量Q可以由Q=πr2λjdn′计算得到，结合式(1)，则任意半径r处的注浆压力为

(4)

1.2 地下通道结构计算模型分析

盾构施工致使底板与土体的接触变得松弛，甚至在局部区段发生脱空。在隧道中轴线上方土体沉降最大(乃至脱空)并向两侧逐渐减小，远离隧道中轴线底板与土体的接触逐渐变得紧密。土体对底板向上的支承力与二者之间接触的紧密程度有关，故表现出相同的分布规律。本文假定，土体对底板的支承力随着距离隧道中轴线长度的增加呈现线性增加的趋势，并在底板与土体的脱空区段取值为0，如图1所示。

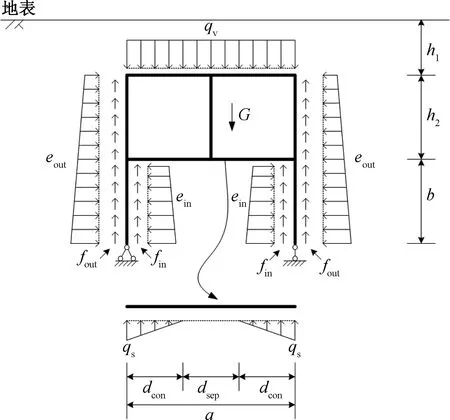
图1 地下道路结构受力分析模型Fig.1 Load model of underground road structure

根据现场监测数据，施工过程中侧墙基本不发生侧移，因而本文假定在整个过程中侧墙受到静止土压力作用，由此可建立地下道路结构的受力分析模型如图1所示。图中，qv表示地下道路顶板以上覆土重力，G为地下道路结构自重，ein、eout分别为围护墙内外两侧的土压力。fin、fout分别为围护墙内外两侧的侧摩阻力，fin=einψ，fout=eoutψ，ψ为侧摩阻力系数，根据许宏发等[14]的研究取0.25。qs表示作用于底板上的土体支承力。土体脱空宽度dsep根据现场施工监测经验进行取值，然后根据地下道路在竖直方向的静力平衡条件可确定底板下方土体支承力qs的分布。

由结构竖向受力平衡，得

(5)

式中，G为地下道路结构自重，Γwall为侧摩阻力的积分域，dcon表示底板一端与土体接触宽度，满足dcon=(a-dsep)/2。

根据图1平面刚架结构，在确定了各部分荷载之后即可求取地下道路结构的内力和变形。

2 注浆压力对底板影响的计算

2.1 计算模型选取

本文以上海地铁10号线同济大学站—四平路站区间盾构隧道与地下通道上下叠置工程为背景，为简化计算，选取上海地区典型软黏土，土层参数如表1所示，掌子面附加推力qj=30 kPa，盾尾注浆压力pj=278 kPa，进行三面围合下盾构隧道施工的变形计算。隧道与地下道路的尺寸及空间布置如图2所示，其中地下道路结构采用C35混凝土(弹性模量3.15e4 MPa，泊松比0.2)，隧道管片采用C50混凝土(弹性模量3.45e4 MPa，泊松比0.2)，注浆体弹性模量为1e3 MPa，泊松比0.2。地下道路底板脱空区域发生在中隔墙下方且关于中隔墙对称，底板上的注浆孔布置如图2所示，dg表示注浆孔中心到中隔墙轴线的横向距离。选取掌子面后方30 m内的地下道路作为一个整体计算底板注浆对道路结构的变形影响，沿地下道路纵向每3 m在中隔墙两侧的底板上布设2个注浆孔。

表1 上海地区典型软黏土力学参数

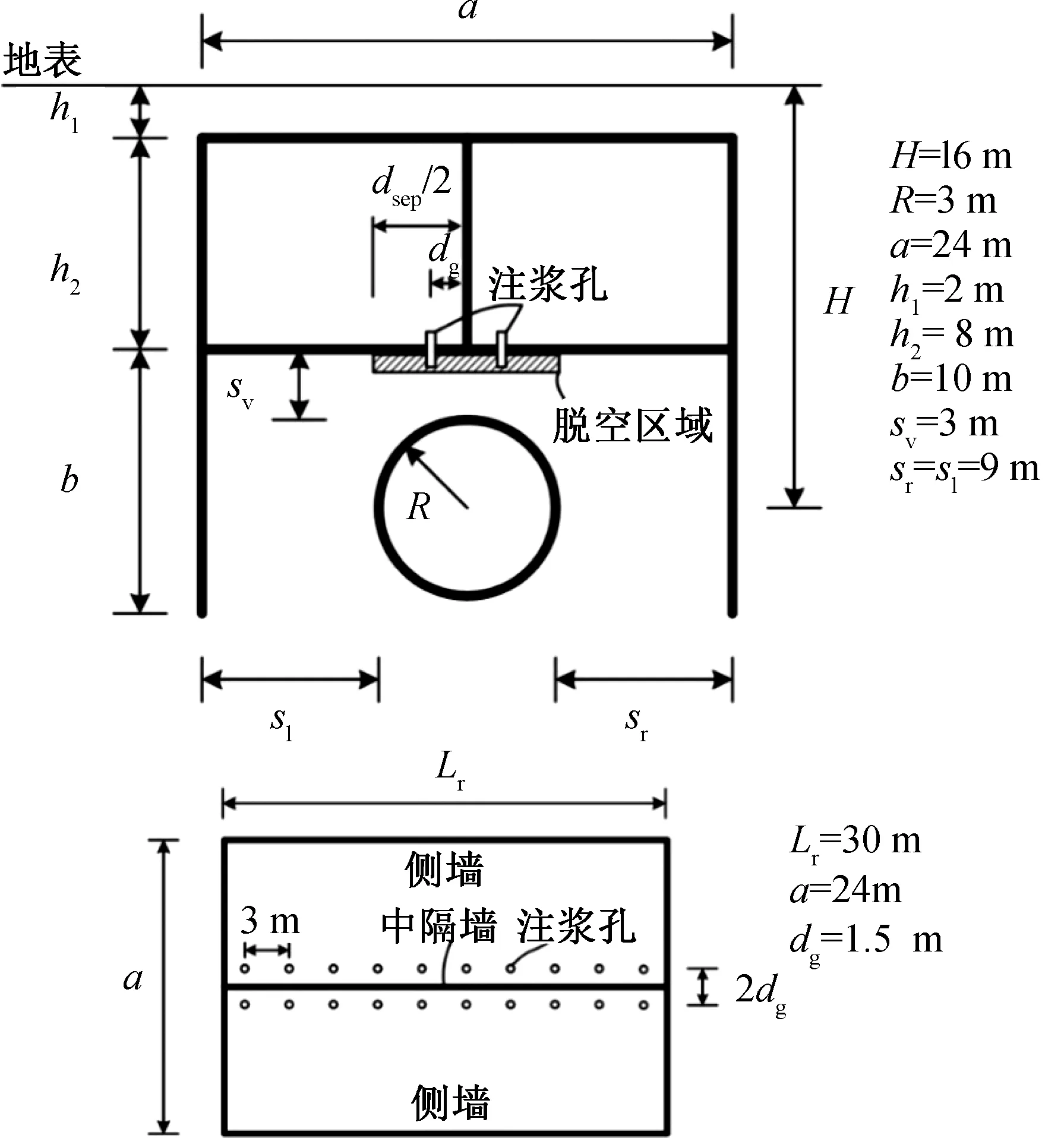
图2 地下道路底板注浆孔布置图Fig.2 Layout of grouting holes in underground road floor

2.2 注浆压力的确定

根据施工现场测量数据发现，当土体损失率ηl=1‰～10‰时，地下道路底板脱空宽度dsep的值很小，不超过1.5 m，此时底板弯矩的增加量也不大，此时底板脱空对地下道路结构的影响不大，因而底板注浆的作用并不明显。只有当土体损失率取值较大(ηl=15‰，dsep=2.5 m；ηl=20‰，dsep=4 m)时，研究底板注浆对地下结构的影响才更有意义。考虑到工程实际，地下道路中隔墙厚度为0.6 m，根据上海地铁10号线与地下通道叠置工程，底板注浆孔外径为325 mm，孔壁厚11 mm，图中dg的取值范围是0.5～1.8 m。

底板注浆的目的是填充底板与下方土体的脱空区域，使底板下方密实以承受上方荷载。然而，过大的浆液压力会引起地下道路底板和盾构隧道结构发生新的附加变形，因此从地下通道结构的设计弯矩出发，确定底板注浆压力的上限。以底板埋深处土体的自重应力σbase为对照，通过不断试算来确定底板脱空区域浆液压力的最大值。

根据《上海城市轨道交通设计规范》[13]的要求，地下钢筋混凝土结构的最大裂缝控制宽度为0.2 mm，其它结构为0.3 mm。依据地下道路底板的截面尺寸和配筋情况可以计算得到底板的系列控制弯矩：①混凝土开裂弯矩Mcr、②裂缝发展至0.2 mm的弯矩M0.2、③裂缝发展至0.3 mm的弯矩M0.3、④极限承载力弯矩Mu。经过不断试算后发现，当底板脱空区域浆液压力达到1.2σbase(216 kPa)时，除去底板两端局部离散点外，底板的最大弯矩恰好不超过0.2 mm裂缝控制弯矩M0.2，如图3所示。此时，地下道路顶板的最大弯矩也不超过M0.2，如图4。因此确定底板下方的浆液分布压力不得超过1.0σbase，即180 kPa。

图3 地下道路底板弯矩Fig.3 Bending moment of underground road floor

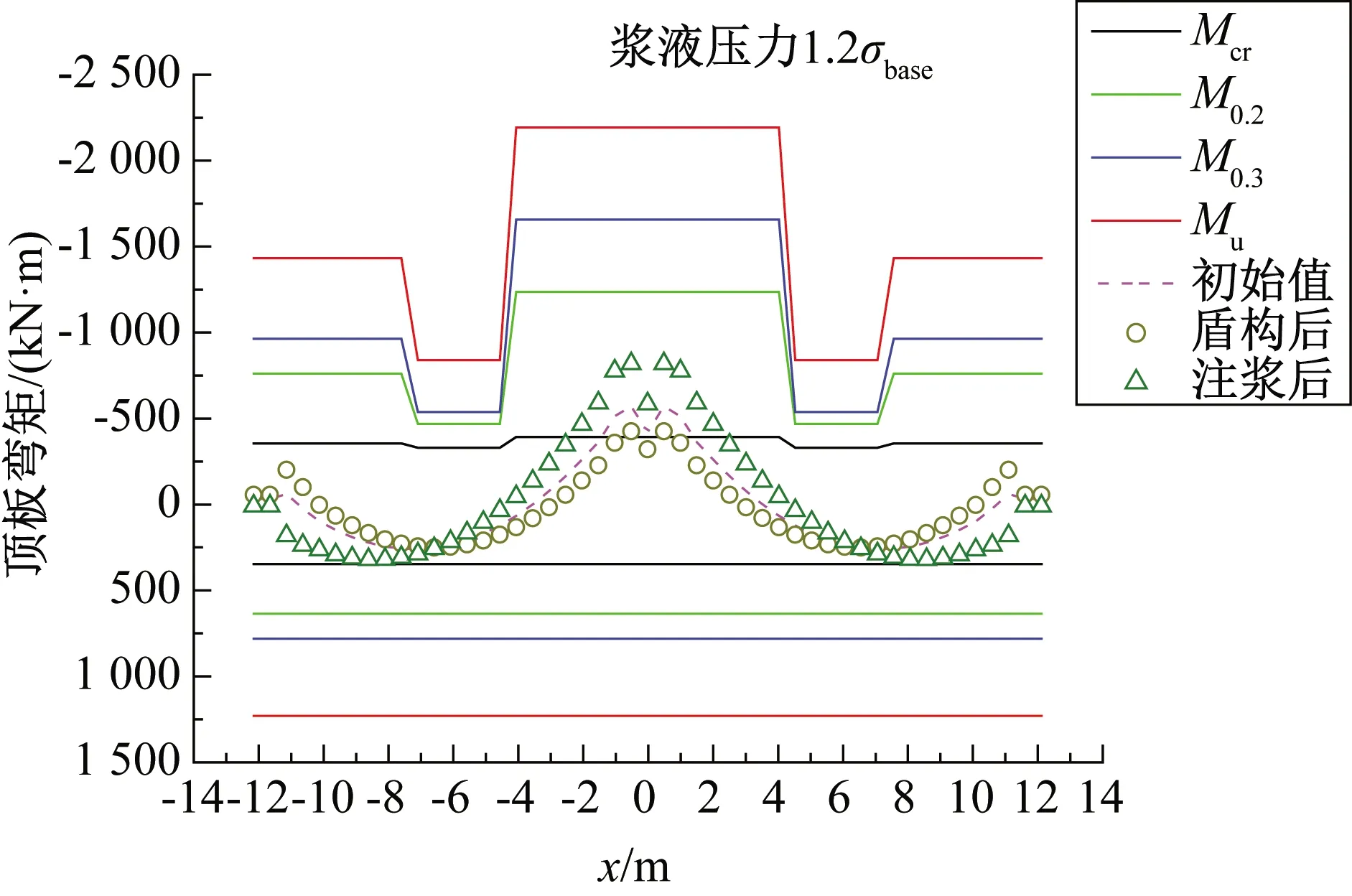
图4 地下道路顶板弯矩Fig.4 Bending moment of underground road roof

根据图2中dg的取值范围是0.5～1.8 m，依次取dg=0.5 m、1.0 m和1.5 m，以180 kPa为注浆压力分别计算注浆后的底板浆液压力。

取底板下方土体孔隙率n=0.2，浆液黏度和水的黏度比β=4，浆液扩散厚度范围内土体中的渗透系数K=5×10-4m/s，浆液注入率λj=1.5。通过计算得到注浆后底板下方形成的浆液压力分布如图5。注浆后30 min，dg取值越大，即注浆孔距离中隔墙越远，底板下方形成的注浆压力越小，但浆液的扩散范围越大，注浆压力在底板下方的分布更加均匀。当dg=1.5 m时，浆液在x=-2～2 m范围内对底板形成比较均匀的压力，压力值在180 kPa左右。当延长注浆时间至60 min后，底板下浆液压力分布的均匀性变差，表现为中隔墙附近压力剧增，远大于其他区域的浆液压力。

为形成对结构受力比较有利的压力分布，取注浆时间为30 min，dg=1.5 m，按照荷载结构法将压力加于地下通道上，计算地下通道内力及变形。此时注浆压力分布于底板横向-5～5 m的范围内，注浆压力对侧墙几乎不产生压力，但侧墙的约束作用仍对地下通道结构的内力存在影响。

图5 底板下方注浆压力的横向分布Fig.5 Lateral distribution of grouting pressure under the floor

3 计算结果分析

通过计算得到土体损失率ηl为15‰时不同底板注浆压力pg下的地下道路顶板和底板的变形情况，包括板件初始变形、盾构施工后变形和底板注浆后变形(图6—图7)。相对于板件初始变形，盾构施工导致的板底脱空，引起了地下道路顶板在中隔墙附近隆起变形减小，顶板在跨中附近下沉变形增大，同时引起地下道路底板的隆起变形全部减小。而底板注浆对板件变形的影响作用与底板脱空正好相反，即注浆压力引起了与底板脱空相反方向的板件附加变形。当注浆压力pg取值为0.5σbase时，由注浆引起的附加变形和由底板脱空引起的附加变形基本抵消，板件的变形值大致回归到初始值。当pg超过0.5σbase后，底板注浆不仅抵消了底板脱空引起的附加变形，还使得板件产生了反方向新的附加变形。以中隔墙处板件变形为例，表2统计了ηl为15‰时底板注浆给板件带来的附加变形相对于初始变形值的变化比例。

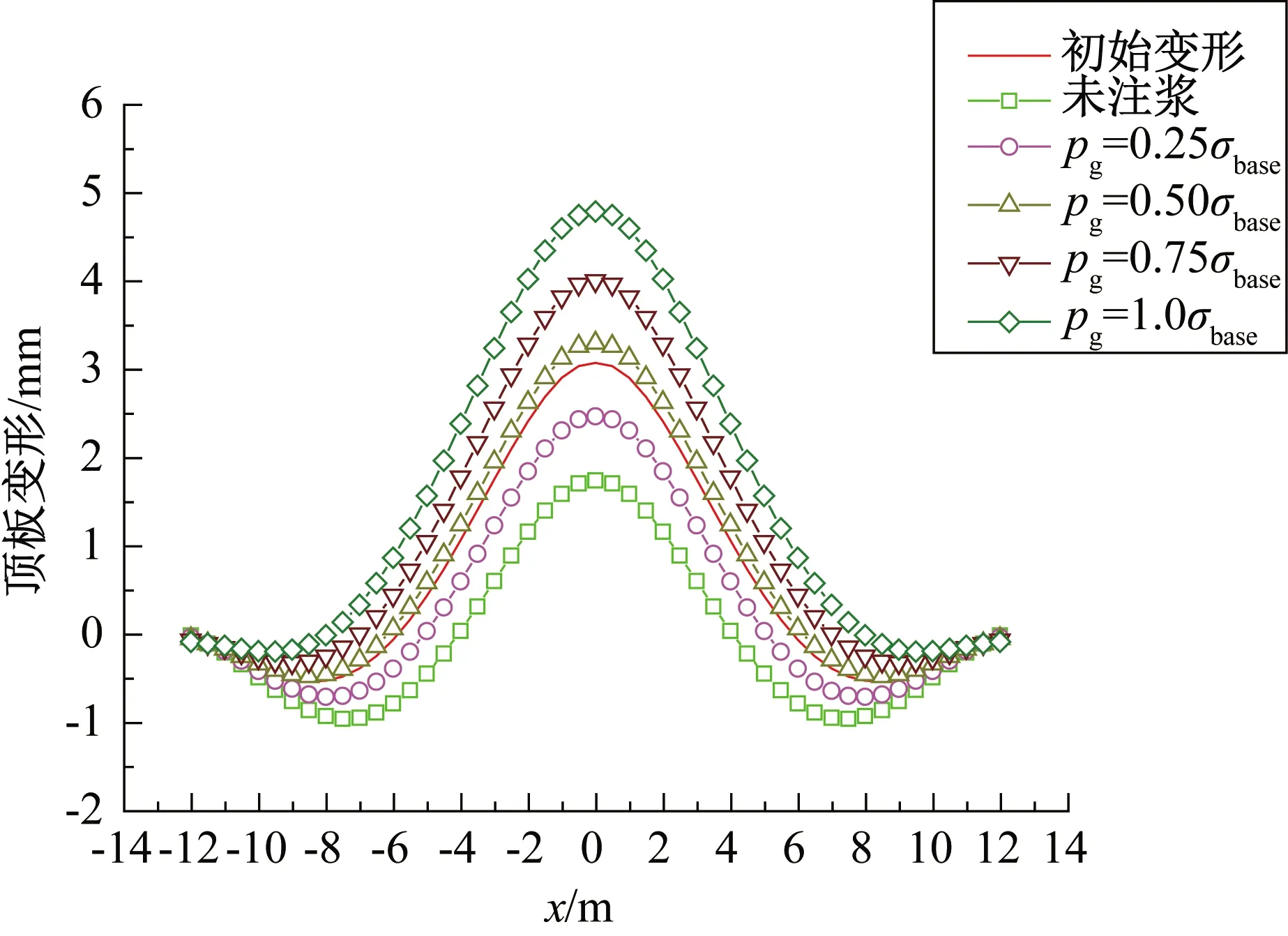
图6 底板注浆引起的顶板变形(ηl=15‰)Fig.6 Deformation of the roof induced by grouting(ηl=15‰)

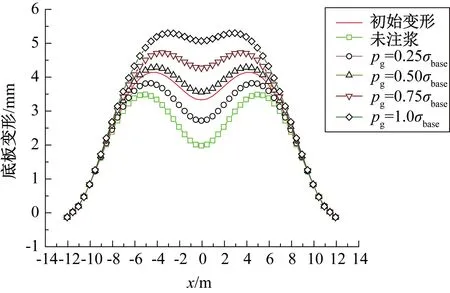
图7 底板注浆对底板变形的影响(ηl=15‰)Fig.7 Deformation of the floor induced by grouting(ηl=15‰)

图8和图9为土体损失率ηl为20‰时顶板和底板的变形曲线。根据中隔墙处板件变形的变化比例，由于土体损失率的增加，盾构施工引起的底板脱空对板件变形的影响作用增强。底板下方脱空宽度的增加，需注入更多的浆液来填充脱空区域，由此也加强了注浆对板件变形的影响。表3统计了中隔墙处板件附加变形相对初始变形的变化比例，ηl=20‰时底板脱空和底板注浆引起的板件附加变形比例约为ηl=15‰时的2倍。

表2 注浆引起的板件附加变形比例(ηl=15‰)

图8 底板注浆引起的顶板变形(ηl=20‰)Fig.8 Deformation of the roof induced by grouting(ηl=20‰)

图9 底板注浆引起的底板变形(ηl=20‰)Fig.9 Deformation of the floor induced by grouting(ηl=20‰)

根据地下道路顶板和底板在不同工况下的弯曲变形，计算得到相应的弯矩，图10—图11为ηl=15‰时的板件弯矩分布情况，盾构施工和底板注浆主要对中隔墙附近的板件弯矩引起了较大的变化，底板脱空使得中隔墙附近的顶板负弯矩(上边受拉)减小了11.38%，使得中隔墙附近的底板正弯矩(下边受拉)增加了36.94%；不同注浆压力导致中隔墙附近的顶板负弯矩(上边受拉)依次增加了-5.18%、1.77%、7.89%、14.52%，导致中隔墙附近的底板正弯矩(下边受拉)依次减小了-16.59%、4.96%、25.08%、46.10%，即底板脱空和底板注浆对地下道路底板弯矩的影响程度比顶板更剧烈。

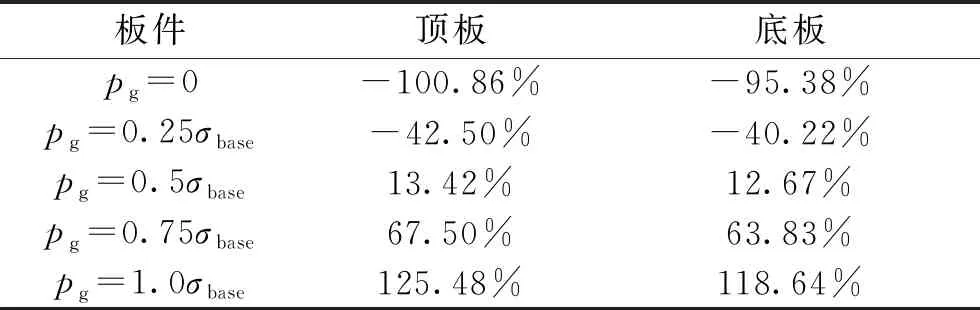
表3 注浆引起的板件附加变形比例(ηl=20‰)

图10 底板注浆引起顶板弯矩(ηl=15‰)Fig.10 Bending moment of the roof induced by grouting(ηl=15‰)

当土体损失率ηl=20‰时，地下道路顶板和底板弯矩分布如图12—图13所示，ηl=20‰时底板脱空和底板注浆对板件弯矩的影响方向和ηl=15‰时相同，但是影响效应有所增强。当ηl=20‰时，底板脱空和底板注浆除了对中隔墙处的板件产生较大影响，还在板件其他位置产生了明显的附加弯矩，附加弯矩的分布范围大大增加。和ηl=15‰时的情况相同，当pg取值0.5σbase时，底板注浆在地下道路顶板和底板上几乎不产生附加弯矩，浆液压力对板件弯矩的影响最小。