立式储罐储液晃动波面振动分析
2020-06-22周利剑卢召红顾孝宋
周利剑, 许 田, 卢召红,2*, 顾孝宋
(1.东北石油大学 土木建筑工程学院, 黑龙江 大庆 163318;2.中国石油管道科技研究中心中国石油天然气集团公司油气储运重点实验室,河北 廊坊 065000;3.中石油昆仑能源有限公司,安徽 合肥 230000)
随着世界经济的发展,各个国家对石油的依赖越来越大,立式储罐作为石油化工重要的储存容器,其在地震作用下的安全性至关重要,而在地震作用下过大的晃动波高是造成储罐破坏的主要原因之一。立式储罐的晃动研究始于二十世纪五六十年代,Housner[1]对储液进行了质量简化,将液体与罐壁部分同步运动的液体质量称为“刚体质量”,相对罐壁晃动的液体部分称为“对流质量”,并通过边界元方法对两质点力学模型进行了理论周期和波高的推导。其中的晃动周期公式被中、美、欧、日等国规范所采用;在Housner理论模型的基础上,Abramson[2-5]等人对罐壁和储液耦合又进行了深入研究,并推导出考虑弹性罐壁的理论波高公式。其中Harou-Housne的晃动波高公式被我国储罐抗震规范[6-7]所采用。中国储罐抗震规范的波高公式是在理论公式基础上并应用于反应谱的形式给出的,其规范波高公式的计算只考量了一阶晃动的参与,并没有考虑多阶振型的叠加,而且规范计算波高对实际工程设计波高的代表性有很大不确定性。因此,本文利用储罐行业常用的有限元软件ADINA对一万方立式储罐作地震作用下的晃动分析。通过不同地震动的输入,来探究立式储罐的晃动形态,并分析了激励波高与储液比及地震动峰值加速度的相关性,其结果对实际工程的波高设计具有一定的价值。
1 有限元模型的建立及地震波的选取
大型立式储罐结构特点是容积大、罐壁薄、高径比小,其在地震作用下结构响应包含许多非线性特征,例如储液和罐壁耦合振动、罐底和基础的相互作用以及储液自身的非线性晃动等都表现出复杂的动力特性。特别是在大型立式储罐试验和规范计算中,因理论规范的假设和试验振动台对输入地震动极限位移的限制,导致很难在不“失真”的情况下研究立式储罐的晃动效应及形态。工程界对于这方面的研究方法有很多,其中有限元模拟是最为有效的方法之一。有限元软件ADINA在液固耦合和非线性方面具有强大的计算能力,国内学者孙建刚等人[8]已证明ADINA对储罐抗震计算的合理性。因此本文采用大型有限元软件ADINA进行一万方立式储罐的晃动数值模拟,来探究晃动形态的特征以及晃动效应与地震动的关系。
1.1 有限元模型的建立
立式储罐根据罐顶形式的不同分为穹顶罐和浮顶罐,大型立式储罐为了安全性以及减少损耗常以浮顶罐的形式建造。而本文目的是研究储罐晃动形态以及地震动频谱特性和激励波高的关系,因此采用敞口罐的形式进行有限元模型的建立。大型立式储罐常采用填砂的环梁基础进行浮放,本文为了便于运行模型并进行大量地震动激励波高的研究,选择采用实体基础进行有限元模型的建立,基础的几何尺寸为直径34 m、高度1 m;储罐储存介质用水来代替石油,从而更接近理论假设的理想流体的状态;一万方立式储罐罐型参数为:罐高17.5 m、罐直径28.3 m、储液高度14 m,储罐罐壁采用4节点壳单元,储液采用等参8节点流体单元,罐底和基础采用接触单元,建立的有限元模型如图1示。

图1 一万方立式储罐ADINA有限元模型Fig.1 ADINA Finite element model of 1×104 m3 vertical storage tank
1.2 地震波的选取
ADINA有限元软件在使用势流体模块进行储罐的地震动时程分析时,需要对储罐以加速度的形式进行地震动输入,也符合规范反应谱法以加速度谱进行地震响应计算的特性。储罐属于特殊设防类别的乙类结构,相关标准规定在进行储罐抗震计算时应采用弹性时程分析进行地震作用下的补充计算。规范反应谱是大量地震动“统计意义”上的加速度拟合平均谱,不能完全反应真实地震动下的结构效应,也不能反应真实地震动下结构的“效应叠加”,特别是反应谱在长周期段的谱值拟合,存在较大争议[9-15]。反应谱长周期段的谱值能不能有效地对长周期地震动响应进行设防,是工程界较为关心的问题,因此时程分析以小样本容量的地震动响应计算来补充结构的抗震计算,这对结构的抗震设防尤为重要。GB 50011《建筑抗震设计规范》[16]中规定时程分析中地震波要依据地震动三要素进行选取,即有效峰值、持续时间和频谱特性。
1.2.1 有效峰值
有效峰值即是图2中的地震峰值加速度,也可用地震影响系数最大值amax除以动力放大系数βmax(一般取2.25)得到。我国的规范计算地震作用时常采用多遇地震进行弹性计算,同构造措施共同满足中震设防的要求,所以在反应谱计算地震响应时运用多遇地震地面峰值加速度进行承载力计算。在时程分析补充计算时,对地震波峰值加速度以设防地震(中震)加速度进行赋值,地震波加速度调整方法如式(1)所示。
(1)
1.2.2 持续时间
一般情况下每条地震波的记录时间都不同。规范规定选波持续时间为从开始到达最大峰值10%的点算起,到最后一次到达峰值10%的点为止;不论是实际强震记录还是合成人工波,有效持时一般按照基本自振周期(5~10)倍,即控制结构顶点位移按基本周期往复(5~10)次;一般的地震波记录持时都能满足持时的要求,对于特长持时的地震波,工程中为加快计算速度,常对长持时地震波进行“抽点”处理,在不改变其频谱特性前提下,尽可能反映真实地震动对结构激励的动态响应。
1.2.3 频谱特性
地震波的频谱特性可用规范给出的地震影响系数曲线表征。设计加速度谱的制定是依据阻尼比0.05,并在大量地震动反应谱曲线拟合的基础上得来的,因此选择地震动的反应谱越接近规范谱,越能贴合规范对结构响应的计算;中国规范中绝对加速度反应谱,由地震影响系数曲线乘以重力加速度即可获得,图3为9度区、第一组的四类场地绝对加速度设计反应谱;我们选取本文所用地震波中的EL波、兰州波、TCU052波和人工波进行反应谱生成,地震波峰值加速度取0.4 g,并与第三类场地设计谱进行对比,如图4所示。从图4可以看出,除了TCU052与反应谱拟合不协调,这也与TCU052为长周期地震动有关,其他三条地震动加速度谱与设计谱拟合就较为合理。
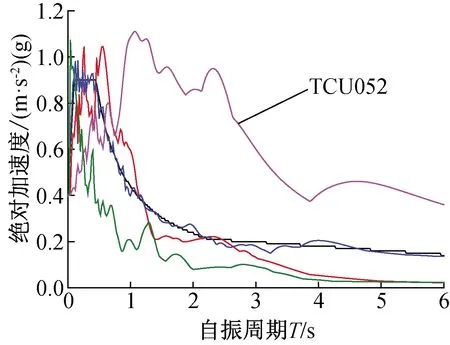
图4 地震波反应谱和设计谱对比Fig.4 Comparison of seismic response spectrum and design spectrum
2 立式储罐的晃动响应分析
2.1 地震动加速度峰值对晃动波高的影响
本节利用有限元软件ADINA对一万方立式储罐作在不同峰值加速度地震动作用下的晃动响应分析,以探究大型立式储罐波高和峰值加速度之间的关系。地震波选取了EL波、兰州波、上海波、TCU052波和人工波,地震波加速度时程如图5所示,每条地震波赋予0.05、0.1、0.2、0.3、0.4 g的地面峰值加速度,得到的晃动波高与加速度峰值如表1所示,并对五条地震波激励波高做与加速度峰值的趋势图,如图6所示。
由图6可知,晃动波高随烈度增加成线性增加。且在相同峰值加速度下,出现从兰州波—EL波—上海波—人工波—TCU波增长的趋势。从表1中可以看出峰值加速度由0.1~0.4 g变化过程中,兰州波的波高变化范围为226~651 mm,即峰值加速度每增加0.1 g,波高增加约为141.7 mm,波高随加速度变化最为缓慢;而TCU波,峰值加速度由0.1~0.4 g变化过程中,波高变化范围为1 517~6 381 mm,即峰值加速度每增加0.1 g,波高增加约为1 621.3 mm,波高随加速度变化最为迅速。输入地震动中TCU052的卓越周期为2.3 s,且含有丰富长周期成分,对储罐的激励波高最大,且激励波高和峰值加速度的变化率也最大。其他四条中短周期波的激励波高相对较小,且仿真中不同峰值加速度和激励波高的关系较试验更加线性化。为探究地震波相邻峰值加速度对应波高的关系,我们对相邻烈度的波高作比值,如表2所示。

图5 输入地震波加速度时程曲线Fig.5 Acceleration time history curve of input seismic wave
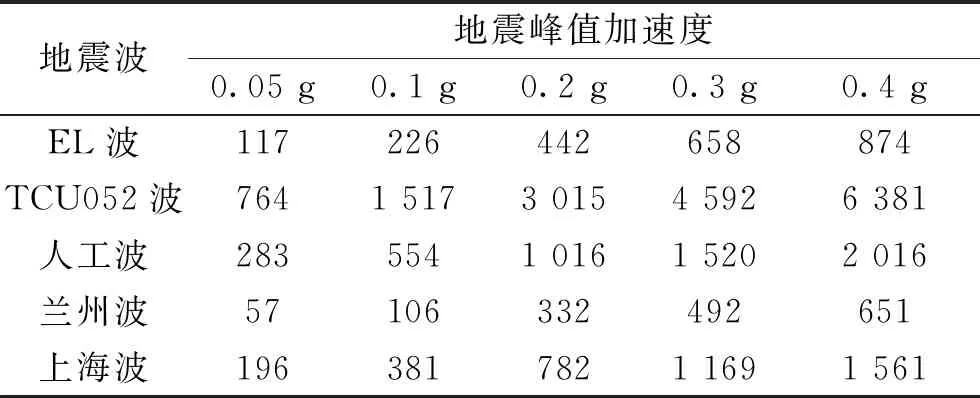
表1 仿真波高 (单位:mm)

图6 波高与峰值加速度趋势关系图Fig.6 Trend graph of wave height and peak acceleration

表2 相邻峰值加速度激励波高比值
注:比例均值=高峰值波高/低峰值波高。
由表2所示,五条地震波在不同加速度对应波高比值和两加速度之间倍数近似相同。即加速度由0.05~0.1 g,0.1~0.2 g,加速度倍数为2,其对应的波高比值也接近于2倍;加速度由0.2~0.3 g, 加速度倍数为1.5,其对应波高比值也为1.5倍;加速度由0.3~0.4 g, 加速度倍数为1.33,其对应波高比值也为1.33倍。在中国储罐规范中波高计算值和影响系数a成一定的关系,而影响系数又通过amax与地震烈度对应加速度成一定的线性关系,这种关系与仿真和试验的关系一致。因此我们可以确定,地震作用下立式储罐的晃动波高随烈度变化而成线性变化,波高的比值和两峰值加速度比值相等。
2.2 不同储液比对晃动的影响
不同国家对立式储罐液位到罐壁上沿的预留空间规定不同,预留空间的大小会影响储罐的储液比,那么不同储液比对晃动是否有较大的影响仍然需要确定。在储罐规范和理论研究中储液比的考虑只体现在了晃动周期公式中,而波高公式中只通过晃动周期考量了储液比。通过计算可知储液比在规范波高计算中影响较小,而在实际地震中,储液比对晃动的影响仍然需要探究。因此,本节利用有限元软件对一万方立式储罐作不同储液比下的晃动模拟,储罐储液比分别为60%、80%和100%,以观察在接近真实地震环境下不同储液比对晃动波高的影响。
输入地震波选择2.1节中的五条地震波,峰值加速度为0.2 g,有限元软件对一万方立式储罐作模态分析和地震激励下晃动仿真,提取的一阶晃动周期和不同地震动激励波高如表3所示。
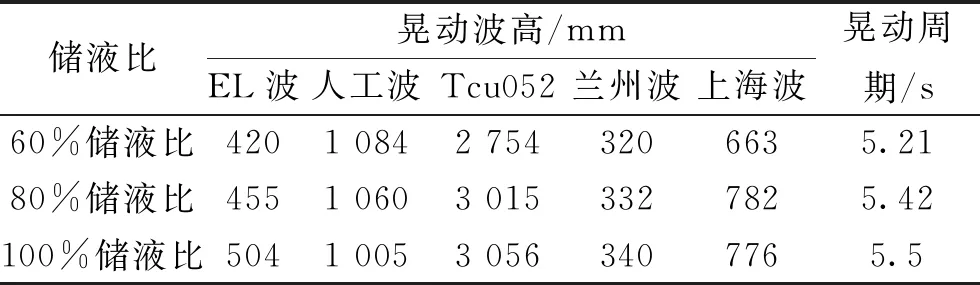
表3 不同储液比的晃动波高和一阶晃动周期
注:储液比=储液高度/储罐高度。
由表3可知,随着储液比的增大,立式储罐晃动波高变化并不明显,晃动周期逐渐增大,但增长幅度较小,从储罐晃动周期的理论公式中可知,储液比对晃动周期的影响由tanh(Hw/D)来体现。通过对tanh(Hw/D)计算可知,储液比的变化占公式计算结果的权重很小,因此从仿真和理论公式中可以得出储液比对晃动周期影响微乎其微的结论;由不同储液比对应的晃动波高值可知,储液比对晃动的影响也较小,每条波对应的三个储液比波高的比率保持在20%以下,平均最大比率为8%,因此储液比的改变对储液晃动波高和储液自振周期的影响都很小,进而在后续的晃动研究中,我们只针对一种储液比进行晃动研究。
2.3 立式储罐储液晃动波面振动分析
地震激励下立式储罐的晃动形态研究一直是晃动控制研究重要的内容,理论的波高简化公式是假设储液一阶晃动,即认为罐壁处晃动波高最大,极值点以类简谐波的形式,做波谷和波峰之间变幅度的往复运动。因此在真实地震动模拟下储罐的晃动形态是否有高阶参与,罐壁处波高是否最大等问题是大幅非线性晃动研究的重要课题。因试验采集设备的限制,液面记录只对特定点进行了时程观测,而对全液面的观测尚不能实现,因此本节借助有限元软件ADINA进行波面振动分析,以探讨地震作用下液面真实晃动形态。提取2.2节中0.2 g各地震动激励下波面径向各点的极值点波高,用于确定波面极值点位置,径向各点极值波高如图7所示。
由图7可以看出不同地震动作用下液面极值点位置不同,5条径向极值波高曲线中EL波和上海波的晃动最大极值点靠近液面中心,即在径向位置15 m左右处达到最大值;兰州波和人工波波高最大极值点在罐壁附近,即在径向位置2.5~5 m和25~27.5 m之间达到最大值;TCU052波的波高极值点在罐壁处,即在0 m和30 m处达到最大值。因此我们可以知道储液晃动是无规律的晃荡,液面晃动极值点的位置也并非在理论假定的罐壁处。我们提取各罐壁处点的波高时程,并对波高时程做傅里叶变化,生成波高频谱图,如图8所示。
由图8可以看出,地震激励下储液晃动是无规律性的,液面晃动极值点越靠近罐壁处,罐壁处液面晃动时程曲线越光滑,这同时也说明一阶振型参与度越大;从频域中可以看出五个频域卓越周期都接近一阶晃动周期5.42 s,可以说明罐壁处液体晃动以一阶晃动为主,但每个频域图主要的频带宽度不同,特别是液面晃动极值在液面中心位置的EL波和上海波最宽,其宽度约为2个卓越周期;其次是液面极值波高稍靠近罐心的人工波和兰州波,其宽度约为1.5个卓越周期;频段最小的是极值点在罐壁处的TCU052波,且频带宽度保持在一个卓越周期的频域附近。因此可以说明储罐晃动为多阶振型的非线性晃动,液面晃动极值点越靠近液面中心,罐壁波高频域宽度越宽,参与叠加振型越多。

图7 液面径向各点极值波高Fig.7 Extreme wave height of radial points of liquid level
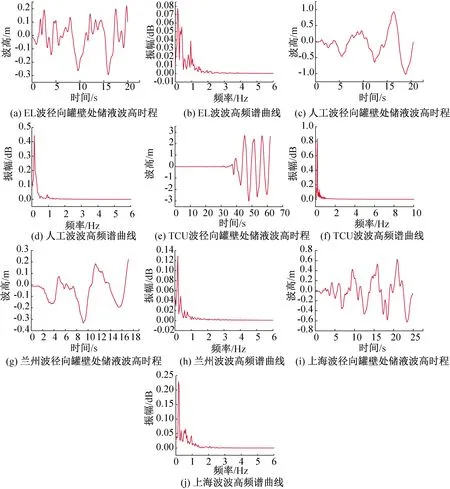
图8 不同地震波激励下罐壁处波高时域和频域Fig.8 Time domain and frequency domain of wave height at tank wall under different seismic wave excitation
3 结论
1)立式储罐在地震激励下的波高与峰值加速度成线性增长,波高增长率约等于峰值加速度的比值,结论与规范、试验相一致;立式储罐的储液比对晃动波高和晃动周期的影响较小,比较贴近理论公式中储液比权重较小的结果。
2)提取一万方立式储罐在五条不同地震波激励下的波高数据,不同地震波激励下,储液波面晃动极值点的位置不同,并非全如理论假设的在罐壁处;储液的晃动是非线性晃动,极值点越靠近罐壁处,叠加振型越少,越靠近罐心处,晃动叠加振型越多,并且极值点在罐心附近的点,其储液晃动形态明显是由高阶振型和一阶振型叠加的结果。
