偏心率对CFRP钢管约束混凝土柱力学性能的影响

李 文，谷长霖，梅宝瑞

(东北石油大学，黑龙江 大庆 163318)

钢管混凝土结构是用钢管包裹混凝土的一种组合结构，从力学性能上看，混凝土与钢管一起承压可以充分发挥混凝土的受压性能和钢管的受拉性能，钢管约束混凝土不但提高了混凝土的抗压强度，也提高了其塑性变形能力和韧性性能。另一方面钢管也可以充当施工模板，节省模板费用。纤维增强复合材料(Fiber Reinforced Polymer, FRP)[1-2]具有自重轻、抗拉强度高、抗疲劳性能优良等特点，随着碳纤维复合材料[3-10]在工程领域越来越多的应用，该结构形式的纤维材料约束钢管混凝土组合柱的探索与研究也成为了一项重要课题。

目前，有关FRP应用于加固方面的研究较多[11-14]，但有关将FRP与钢管组合为复合管约束混凝土的相关研究相对较少。同时，在实际工程中的构件柱通常受轴力和弯矩的共同作用，故可以等效为一个偏心的轴向力，因此研究偏心率对构件的影响显得尤为重要。本文研究CFRP钢管约束混凝土柱力学性能，分析偏心率对CFRP钢管约束混凝土柱的影响规律，为实际工程应用提供理论依据。

1 有限元模型

1.1 有限元模型的建立

CFRP为各向异性材料，其在达到极限拉应变之前定义为理想线弹性材料，当超过极限拉应变时材料发生破坏，承载力下降为0。根据简化计算需要，钢材采用的是双线性随动强化模型，屈服准则采用Von Mises屈服准则[15-16]。混凝土采用塑性损伤模型。

混凝土定义为八节点缩减积分格式的三维实体单元C3D8R，钢管定义为壳单元S4，CFRP布定义为膜单元M3D4[17]。端板定义为三维实体单元，其厚度为20 mm。网格的密度划分对试验结果有一定的影响，经过不断调整网格大小，取两次分析结果相差较小的网格大小，对组合柱和刚性端头进行网格划分，设置全局单元尺寸为0.1。划分网格后的CFRP与核心混凝土部分(图1)。

图1 网格划分Fig.1 The diagram of gridding

本文借鉴文献[18]的方法，在柱上下底面分别施加两个刚性垫板，在两端刚性垫块上创建两个偏心参考点，通过施加位移荷载来施加偏心荷载，将参考点与刚性垫块进行耦合，对柱顶参考点约束X、Y方向位移，在参考点上施加Z方向位移荷载，对柱底参考点约束X、Y、Z三个方向位移(铰接)，如图2所示。

图2 边界条件Fig.2 The diagram of the boundary conditions

1.2 试件设计参数

根据相关规定，本文钢管厚度取6 mm，钢管外径取500 mm，柱高取800 mm；采用一层加固CFRP布，其具体参数如下：理论厚度为0.167 mm，弹性模量为2.3×105N/mm2，密度为1.8 g/cm3，泊松比为0.17。

两组长细比分别为22.4、28。A组及B组偏心率都分别为0.3、0.6、0.9、1.2。钢管材料性能参数及所需模拟的试件参数见表1和表2。

表1 钢材性能

表2 构件分组

1.3 模型验证

将参考文献[7]试验数据与有限元模拟结果对比，表3给出了试件在ABAQUS计算所得承载力与试验所得承载力，可以看出模拟极限承载力与试验承载力比值介于0.83～1.04之间，平均值为0.96，均方差为0.06，误差在可接受的范围内，说明模拟与试验结果比较吻合，因此可进行接下来的模拟运算工作。

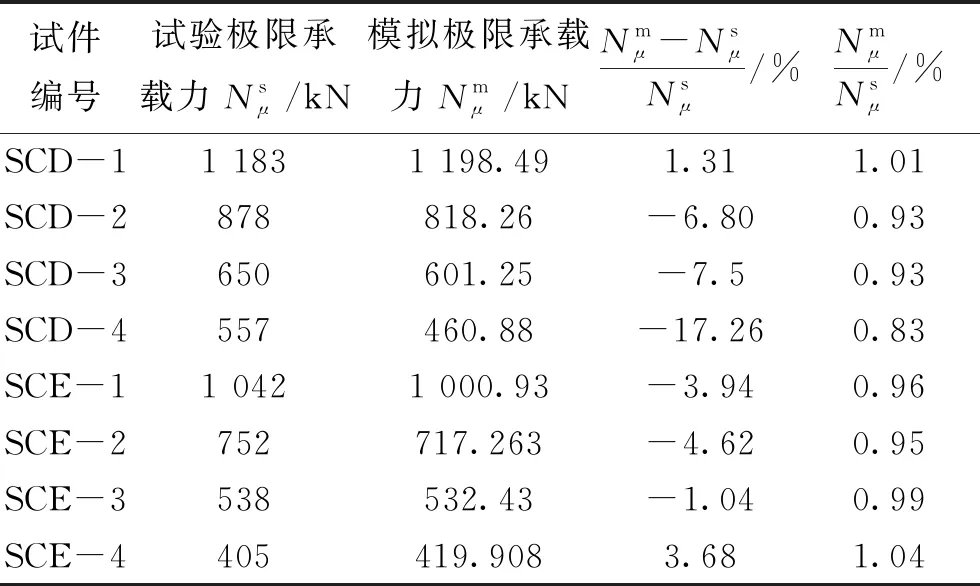
表3 模拟对比验证数据

2 有限元分析结果

2.1 不同偏心率作用下构件的等效应力云图分析

图3为不同偏心率作用下极限承载力下各部件的应力云图。环向CFRP的最大等效应力均达到极限强度1 265 MPa，随着偏心距的增大，达到极限应力的区域向柱中区域缩小，环向CFRP的紧箍力减小。钢管均达到了屈服强度，钢管的等效应力转变为向柱中距荷载较远一侧扩大，柱中两侧最大应力分布相差越来越小。主要原因是偏心率较小时，柱子距荷载较远一侧因弯矩产生的拉力较小，当偏心率增大时，相同荷载产生的弯矩增大，对钢管另一侧的拉应力也相应增大。对于混凝土区域，当偏心率为0.3、0.6、0.9、1.2时，最大压应力值分别为88.2、75.9、72.0、70.3 MPa，最大拉应力值分别为32.5、41.7、45.5、43.1 MPa，可以看出最大压应力值随着偏心率增高而降低。最大拉应力在偏心率0.3～0.9之间随着偏心率增大而增大，在偏心率0.9～1.2之间略有下降。随着偏心率的增大，受拉区域相对于受压区域有所增大。

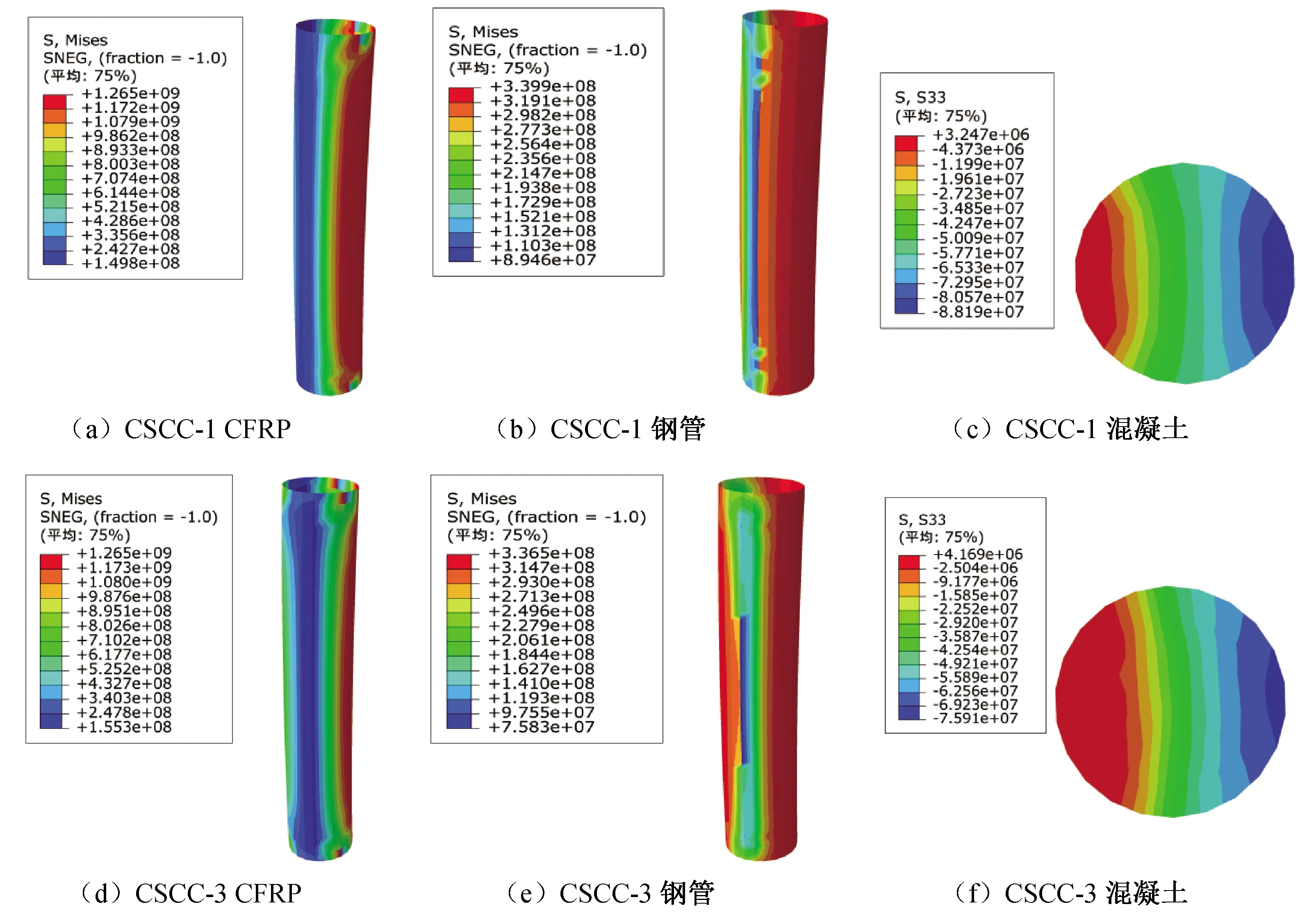
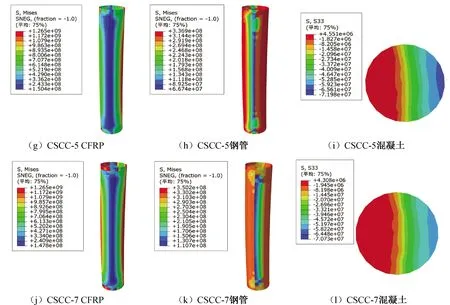
图3 不同偏心率下试件应力云图Fig.3 The diagram of stress nephograms of specimens with different eccentricity

偏压柱到达极限承载力时，截面上出现不同程度的塑性变形，随着偏心距的增大受压区减小，压区塑性应变也相应变小，塑性变形变小，导致被动约束紧箍力也就减小，即随着偏心距的增大，被动约束的紧箍力减小。由于横截面受压区应力越靠近受压侧边缘应力值越大，塑性变形越大，因此对于同一截面上的紧箍力是不均匀的。

2.2 荷载-挠度曲线

荷载-挠度曲线如图4所示，可以看出偏心率对柱的荷载-挠度曲线形状有较大的影响，偏心率大的构件极限力较小，上升段整体斜率及极限承载力对应的挠度较小，即刚度较小。如图4(a)所示，在长细比为22.4，偏心率为0.3时，随着极限承载力的增加，挠度呈近似线性变化，当极限承载力达到9 900.87 kN时，曲线呈下降趋势；当长细比为22.4，偏心率为0.6，极限承载力仅达到6 341.55 kN时，曲线即开始下降。当长细比一定时，随着偏心率的增加，荷载-挠度曲线整体呈下降的趋势。主要原因是随着偏心率增加，截面的受拉区及受压区应力分布发生了改变，受拉区相对受压区增大，在较小的荷载下受拉区混凝土就已经开裂，导致其极限承载力降低。

2.3 极限承载力对比

由表4可知偏心率对极限承载力有较大的影响，A组试件CSCC-3比CSCC-1降低了35.9%，CSCC-5比CSCC-3降低了32.7%，CSCC-7比CSCC-5降低了27.7%；对比B组数据的极限承载力有着同样的降低趋势，可知随着偏心率的增大柱的承载力降低，且降低幅度减小；偏心率对不同长细比的构件影响不同，长细比为28时，试件的承载力相应地整体降低。

图4 不同偏心率下荷载-挠度曲线Fig.4 The diagram of load-deflection curves at different eccentricity

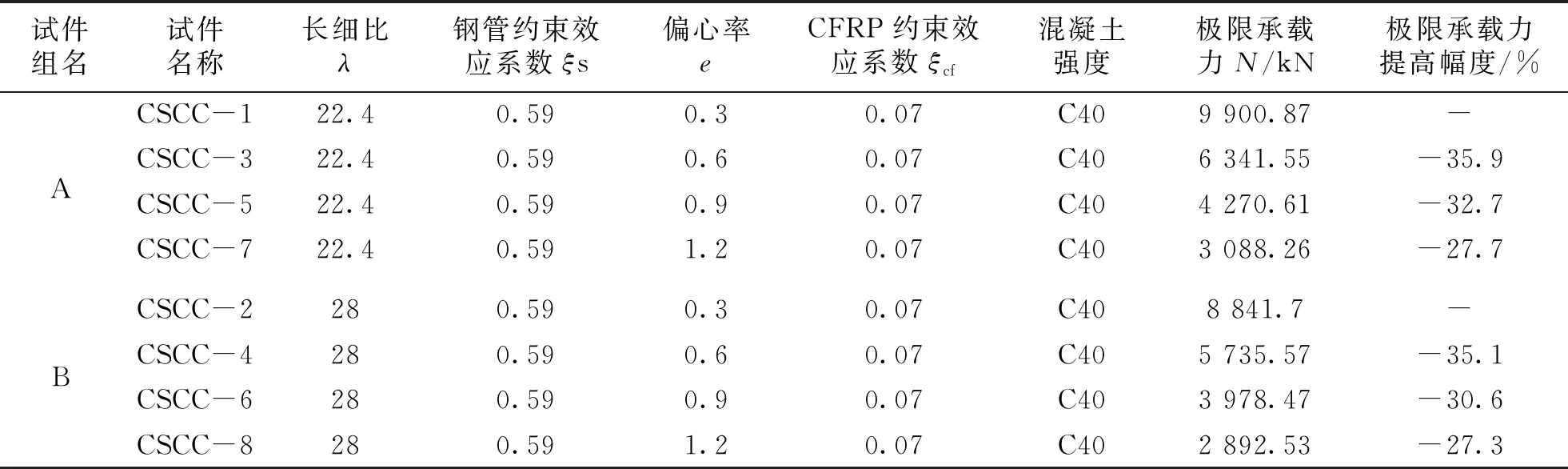
试件组名试件名称长细比λ钢管约束效应系数ξs偏心率eCFRP约束效应系数ξcf混凝土强度极限承载力N/kN极限承载力提高幅度/%ACSCC-122.40.590.30.07C409 900.87-CSCC-322.40.590.60.07C406 341.55-35.9CSCC-522.40.590.90.07C404 270.61-32.7CSCC-722.40.591.20.07C403 088.26-27.7BCSCC-2280.590.30.07C408 841.7-CSCC-4280.590.60.07C405 735.57-35.1CSCC-6280.590.90.07C403 978.47-30.6CSCC-8280.591.20.07C402 892.53-27.3

根据图5可以看出随着偏心率的增大，曲线斜率的绝对值逐渐减小，即随着偏心率的增大，极限承载力的降低幅度变小。

图5 偏心率e-极限承载力N关系曲线Fig.5 The diagram of eccentricity e-ultimate bearing capacity N relation curve

3 结论

1)随着偏心率的增大，受压区减小，压应力整体减小，其受压区塑性应变也就越小，导致被动约束紧箍力也就减小，即随着偏心率的增大紧箍力减小。

2)由于截面受压区应力越靠近受压侧边缘应力值越大，塑性变形越大，紧箍力在同一个截面上是不均匀的。

3)随着偏心率的增大，受拉区域相对于受压区域有所增大，构件的极限承载力降低，且降低幅度减小，偏心率与极限承载力呈非线性关系。

4)极限承载力随着长细比的增大而整体减小。