PKPCA-LRM在滚动轴承性能退化评估中的应用

王 萌，王奉涛

（大连理工大学机械工程学院，辽宁 大连 116023）

1 引言

滚动轴承是旋转机械设备最重要的零部件之一，它的运行状态直接影响到整个机械设备的状态。据不完全统计，机械设备故障中，约有30%是由滚动轴承故障引起的。因此，对滚动轴承的运行状态进行监测，建立滚动轴承的可靠性曲线是非常有必要的。

基于状态监测的滚动轴承寿命理论是当前的重点研究方向[1]，且寿命预测模型中比例故障模型和Logistic回归模型应用最广泛。文献[2]以均方根值和峭度值作为威布尔比例故障模型的协变量对铁路机车轮对滚动轴承的可靠性进行了评估。文献[3]利用全寿命数据通过混合威布尔比例故障模型，来预测含有多个失效形式的机械系统的剩余寿命。文献[4]采用数据驱动的方法研究了基于威布尔和人工神经网络的轴承寿命预测。文献[5]研究了基于设备比例故障模型和支持向量机的机械性能退化评估。Logistic回归模型相较于威布尔比例故障模型估计参数少，准确率高，因此，选取参数估计较少的Logistic回归模型对滚动轴承进行可靠性评估。

在以往研究中，Logistic回归模型的协变量往往都是时域的几个特征值。但是单一的评价指标并不能完全表征轴承的退化过程。提出应用概率核主成分分析（Probabilistic kernel principal component analysis，PKPCA）的方法综合时域、频域和时频域的特征值，混合域特征值更能表征轴承的退化状态，并通过试验验证了该方法的有效性。

2 理论基础

2.1 概率核主成分分析

概率核主成分分析（PKPCA）将数据通过核函数映射到高维空间，在高维空间中重新推导PPCA算法，克服了PCA缺少概率模型和缺失高阶统计量的不足[6]，具体算法如下：

（1）假设｛x1，x2，x3，…，xn｝为数据空间 Rd中的训练数据，通过映射函数φ将训练数据映射到高维数据空间Rf，得到高维数据集 φ=［φ1，…，φn］，其中 f>d。则高维数据协方差矩阵为：

其中，k=1，2，…，N

（2）定义矩阵 K∈RN×N，使 K=φφT。

（3）在高维空间中重新推导PPCA算法，隐变量模型为：

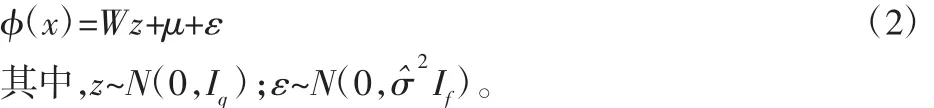
（4）则随隐变量z变化的高维空间数据φ（x）的随机概率分布为：

可得训练数据φ（x）的最大似然函数为：

（5）由最大似然估计可以得到μ，W和σ2的估计值，将其作为参数初始值，用EM迭代算法可获得模型精确值。

2.2 Logistic回归模型

Logistic回归模型中，yt取0、1表示事件仅有的两种独立情表示协变量，m 为协变量个数，t=1，2，…，n为时间坐标。则事件不发生（yt=1）的条件概率为：

式中：β0—截距（或称常数项）；βj—协变量xj（t）对应的回归系数；

exp（.）—以自然对数（2.71828）为底的指数。

由极大似然估计方法求出 β0，β1，β2，…，βm后，滚动轴承的可靠度函数可表示为：

3 方法步骤

（1）特征参数选取：提取表征轴承退化状态的时域、频域和时频域的特征值组建高维混合域特征集。

（2）求取相对特征值：求取高维混合域特征集对应的相对特征，组成高维混合域相对特征集。

（3）归一化处理：对高维混合域相对特征集进行最小--最大标准化的方法来消除不同指标之间的量纲影响。

（4）概率核主成分分析：对经过归一化之后的高维混合域相对特征集进行概率核主成分分析，选取累计贡献率超过90%的主元作为Logistic回归模型的协变量。

（5）可靠性评估：根据概率核主成分分析得到的主元对Logistic回归模型参数进行估计，建立Logistic回归模型，对轴承的可靠性进行评估。算法流程图，如图1所示。

图1 算法流程图Fig.1 The Flow Chart of the Proposed Method

4 试验验证

4.1 滚动轴承试验台介绍

图2 试验装置Fig.2 Test Bench

该试验共进行了三次，选取实验一轴承3的数据进行分析，停机时轴承3内圈发生严重故障，如图3所示。实验一轴承3全寿命振动信号，如图4所示。从图中可以看出在轴承严重故障时期振动信号的幅值明显增大。

图3 实验一轴承3内圈严重故障Fig.3 Inner Race Defect in Bearing 3 Test_1

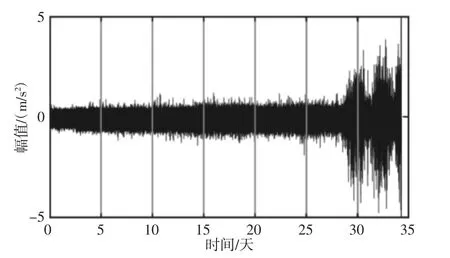
图4 轴承全寿命振动信号Fig.4 Full Life Vibration Signal of Bearing

4.2 协变量选取方法研究

根据滚动轴承振动信号的特征，提取能反映滚动轴承退化状态的13个时域特征值，2个频域特征值和1个时频域特征值。

时域特征：均方根值、峰值、峭度、标准差、方差、绝对均值、平均功率、方根幅值、峰值指标、脉冲指标、裕度指标、峭度指标、THIKAT。

频域特征：重心频率，均方频率。

时频域特征：三层小波包分解后归一化能量最大子带的样本熵。

1.2.1 pH的测定 称取10.0 g制备好的土壤，置于50 mL的高脚烧杯中，加入25 mL无二氧化碳水。将容器密封后于磁力搅拌器上搅拌5 min，静置1 h后，用校正好的pH计进行测定。

并求取相对特征值[9]来降低轴承的个体差异，轴承全寿命数据相对特征值，如图5所示。

图5 滚动轴承全寿命相对特征值Fig.5 Relative Characteristics of Whole Lifetime

采用概率核主成分分析的方法对挑选的混合域相对特征集进行降维。结果，如表1所示。

表1 概率核主成分分析分析结果Tab.1 The Result of PKPCA

由表1可以看出，高维混合域相对特征集经过PKPCA降维后前二个主元的贡献率已经达到了90%以上，因此选择前二个主元作为Logistic回归模型的协变量。将前两个主元投影到二维空间效果，如图6所示。

图6 第1，2主元滚动轴承状态图Fig.6 The Top Two Principal Components

从图6第一主元可以看出轴承运行过程中的不同时期（正常期、早期故障、中期故障、严重故障）从小到大依次排列，间隔明显，反映了轴承的退化趋势。从第二主元上，可以看出早期故障的趋势特别明显，这是因为峭度值，峰值等特征指标对早期故障特别敏感。

为进一步验证PKPCA对滚动轴承退化状态表征的优越性，以美国凯斯西储大学轴承外圈故障信号为例，用电火花在轴承表面加工损伤直径为0.1778mm、0.3556mm、0.5334mm的单点损伤模拟轴承早期故障状态、中期故障状态和严重故障状态[10]，分别选取各个故障状态和正常状态的信号各30组，提取其时域、频域和时频域的特征值，组成（16×120）的高维混合域特征集。采用PKPCA和PCA的方法，对高维样本数据进行处理，选取能够表征轴承退化状态的前两个主元绘制二维图形，如图7所示。

图7 PCA和PKPCA分类结果Fig.7 The Classification Result of PCA and PKPCA

图中：各个线分别对应轴承的正常、早期故障、中期故障和严重故障阶段。

从PCA和PKPCA的对比中可以发现，PKPCA对于轴承不同退化状态的故障具有明显的分类效果，类间样本的距离较远，而PCA分类中正常期和中期故障状态重叠在一起，且类间样本的距离较近，不利于区分轴承的不同退化阶段。

将PKPCA降维得到的前两个主元作为Logistic回归模型的协变量与将峭度值和均方根值作为Logistic回归模型协变量得到的可靠性曲线进行对比分析，如图8所示。

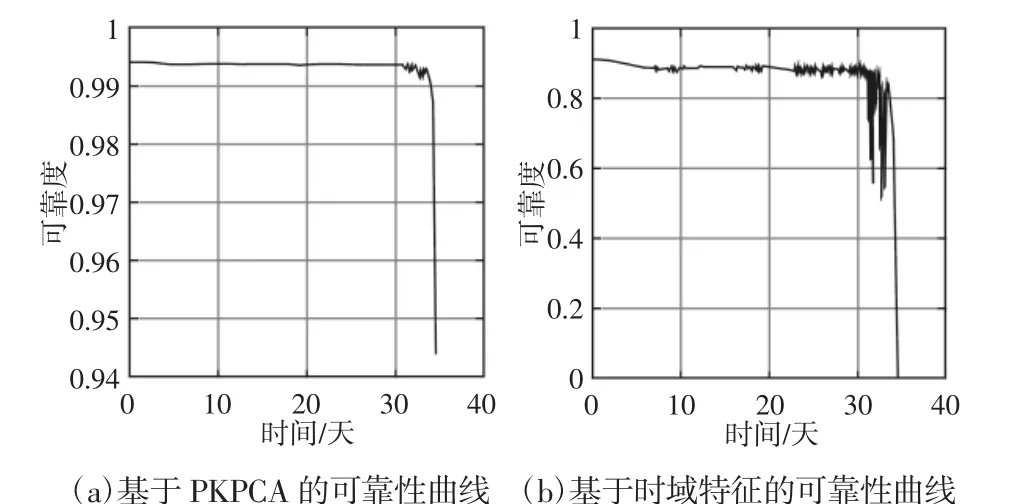
图8 基于PKPCA和时域特征值的Logistic回归模型可靠度曲线Fig.8 Reliability Curve of LRM Based on PKPCA and Time-Domain Characteristics

图中：各个线分别对应轴承的正常期、早期故障、中期故障和严重故障阶段。

从图8中可以看出基于PKPCA的轴承可靠性曲线比基于时域特征的轴承可靠性曲线更能反映轴承的实际退化趋势。在轴承正常运行阶段，基于PKPCA和基于时域特征的轴承可靠性曲线变化比较平稳，能够体现出轴承发生缓慢退化的过程。

在轴承早期故障阶段，基于PKPCA的轴承可靠性曲线稳定平缓下降，而基于时域特征的轴承可靠性曲线，则出现剧烈的波动，这是由于时域特征的峭度值对于轴承的早期故障比较敏感，导致可靠性曲线出现较大波折。在轴承中期故障阶段，轴承的性能显著退化，基于PKPCA的可靠性曲线要比基于时域特征的可靠性曲线更加稳定。在轴承严重故障阶段，基于PKPCA和基于时域特征的可靠性曲线都急剧下降。综上所述，基于PKPCA的轴承可靠性曲线融合了轴承时域、频域和时频域的特征，更能表征轴承的实际退化趋势。而基于时域特征的轴承可靠性曲线，受单一特征指标的影响，在表征轴承退化趋势的过程中存在一定的局限性。

5 结论

通过试验验证了PKPCA-LRM方法在滚动轴承可靠性评估中的有效性，得到如下结论：（1）PKPCA相较于PCA，可以更好的区分轴承不同退化阶段的故障状态，具有更好的类间散度，聚类效果好。（2）相对特征值可以降低轴承制造、安装和实际工况差异的影响，使得轴承之间的各体差异对混合域特征集构建的影响大大降低。（3）将基于混合域特征值的概率核主成分分析与Logistic回归模型结合，建立了滚动轴承的可靠性曲线，可以更加全面的表征轴承的退化状态。