新一代GPS 下的平行度误差投影迭代评定法

王世强，郑 鹏

（郑州大学机械工程学院，河南 郑州 450001）

1 引言

位置误差是几何误差的重要组成部分，它主要包括平行度、垂直度、同轴度、倾斜度等。位置误差不同于单一要素引起的方向误差，它由多个关联要素（基准要素、被测要素）所确定[1]。在评定位置误差的时，首先需要确定基准要素，然后以基准要素为约束来对被测要素进行评估，最后的结果就是所求的位置误差值。

平行度属于位置误差，在我们的日常生活、工业应用中具有十分重要的作用。平行度是指被测要素相对于具有确定方向的理想要素的变动量，它主要包括有：线对线的平行度、线对面的平行度、面对线的平行度、面对面的平行度[2]。其中面对面的平行度是其中最复杂的，我们如果掌握了面对面的平行度检测方法就会很容易的推理出来其他三种的检验方法；同时面对面平行度也是我们在实际应用中最常见的类型。综合两种情况，主要介绍的面对面平行度的研究。

平行度检测原则主要是定向最小区域原则：首先确定基准面，然后以基准面为标准建立两个平行于基准面的平面，此时如果两平行平面全包括被测要素的所有点，那么它们之间的最小距离就是我们所求的平行度。在这里根据已知条件（过被测点且平行于基准面）可以构建一系列平面特征方程，然后找出能够包括所有检测点的两个平行平面，这两平行平面的距离就是所求的平行度误差。为了减少计算量，在迭代的基础上引入了投影法，将三维的空间平面转化成二维的平面上的直线来解决，这一方法减少了计算量，增加了计算速度。

2 新一代GPS下平行度的评定过程

在新一代GPS下评定误差的过程中，特引入操作、操作算子这一概念，从而能明确的定义和规范产品几何技术规范这一概念。因此在新一代GPS条件下对形位误差的检测过程中，首先要确定它的操作算子构建，然后以此为基础进行数学建模求解。操作是以计量学为单位的新一代GPS中为体现要素、获取规范值和特征值，面对表面模型或实际工件表面而进行的一种特别的处理方法。操作主要包括要素操作和评估。要素操作包括：分离、提取、滤波、拟合、集成、构建。评估操作是要素操作后所获得的值是否能够达到几何要素要求的过程。位置误差是有多个要素相互影响的误差形式，在评定其过程中首先应该定义评定的基准，然后再对被测要素进行评定。平行度是位置误差中的一种，其评定过程主要有两个过程：基准的建立和平行度的评定。

2.1 基准的建立

2.1.1 分离

从被测零件中找出基准面，然后把基准面从被测零部件分离出来，以被分离出的该面为基准展开研究，如图1所示。

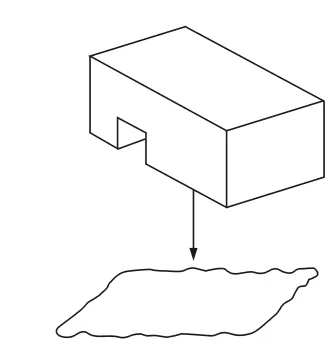
图1 基准面的分离操作Fig.1 Separate Operation of Reference Surface

2.1.2 提取

提取是从上一步分离出的平面中按照一定的方法提取若干个点Ai（xi，yi，zi）的操作过程。我们通过提取的这些点来表达所分离的平面，以便计算机进行数据处理。提取操作，如图2所示。

图2 提取操作Fig.2 Extraction Operation

2.1.3 拟合操作

拟合是用提取的点通过一定的准则来表达理想要素的过程。通过这个操作过程能够达到对基准要素的表达替换，如图3所示。

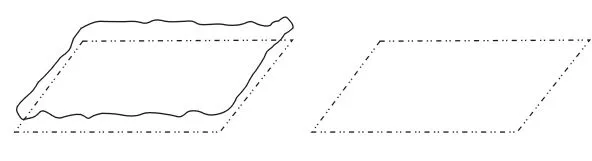
图3 拟合操作Fig.3 Association Operation

设Ai（xi，yi，zi）为本次操作过程中所提取的点的集合，通过最小二乘法所拟合的方程设为：Axi+Byi+Czi+D=0

2.2 平行度的评定

平行度就是以基准平面为条件来约束被测要素，从被测要素中分离出来一个平面，然后通过提取、滤波、拟合、组合、构建、评估等过程来判断被测要素相对于基准要素的平行度是不是达标。被测要素操作算子的构建步骤如下。

2.2.1 分离

从被测要素中分离出要研究的要素，从而确定被测要素的组成要素及其测量界限。分离操作，如图4所示。

图4 分离操作Fig.4 Separate Operation

2.2.2 提取

用一定的方法从第一步分离出的平面，提取是从第一步分理出的被测平面中提取到一定的点Bj（xj，yj，zj）。提取操作，如图5所示。

图5 提取操作Fig.5 Extraction Operation

2.2.3 拟合

拟合是以基准面为标准来求解被提取的平面相对于该基准面的平行度。拟合操作是操作算子构建一个十分重要的环节，不同的拟合方法直接决定了平行度的准确性和精确性。拟合方法大致有以下几种：最大内切法、最小外接法、最小二乘法、最小区域法等。平行度误差是是位置误差中的一种，在拟合方法上本论文采用定向最小区域法。设Bj（xj，yj，zj）为被测平面上任意一点，设被测平面方程为：A1x+B1y+C1z+D1=0。

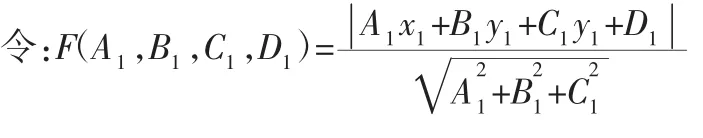
上式即为点Bj（xj，yj，zj）到A1x+B1y+C1z+D1=0的距离，利用最小区域法构建被测平面的优化拟合函数如下：

E=Min（F（A1，B1，C1，D1）Max-F（A1，B1，C1，D1）Min）

拟合操作，如图6所示。

图6 拟合操作Fig.6 Association Operation

2.2.4 评估操作

评估就是以基准为参照对被测要素进行评估，如下如所示，通过上式给出的拟合函数来求解，最后求出的平行于基准面的两平行平面的距离就是我们所要求的数据。评估操作，如图7所示。

图7 评估操作Fig.7 Evaluation Operation

通过上一步知道拟合出的函数为：

E=Min（F（A1，B1，C1，D1）Max-F（A1，B1，C1，D1）Min）

根据被测平面平行于基准平面以及Bj（xj，yj，zj），可求出E即为我们所求得到的平行度，然后与该零件要求的平行度作对比得出该零件是否合格的结论。

3 投影迭代法

3.1 迭代法

迭代法又称为辗转法点，是一种不断用变量的旧值替换新值的过程[5]。迭代的本质是一种重复性的反馈活动，其目的是获得新值并使新值不断逼近最终结果。在迭代的过程中以初始值为计算量得到一个结果，如果这个结果能够用满足我们限定条件的要求，那么将这个结果替代初始值重新展开计算，这就是一个迭代过程。

在运用迭代法计算过程中主要经过一下三步骤：

（1）确定迭代变量；

（2）建立迭代方程；

（3）迭代计算，求出结果。

根据迭代法的思想，现在利用迭代法求解平面度误差的大小。

3.1.1 基准面的求解

已知被测基准点为Ai（xi，yi，zi），其中i=0，1，2，…，n-1。设基准平面为：z=Ax+By+C，则基准点到空间平面的距离为：

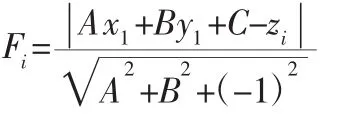
用最小二乘法求解，即：

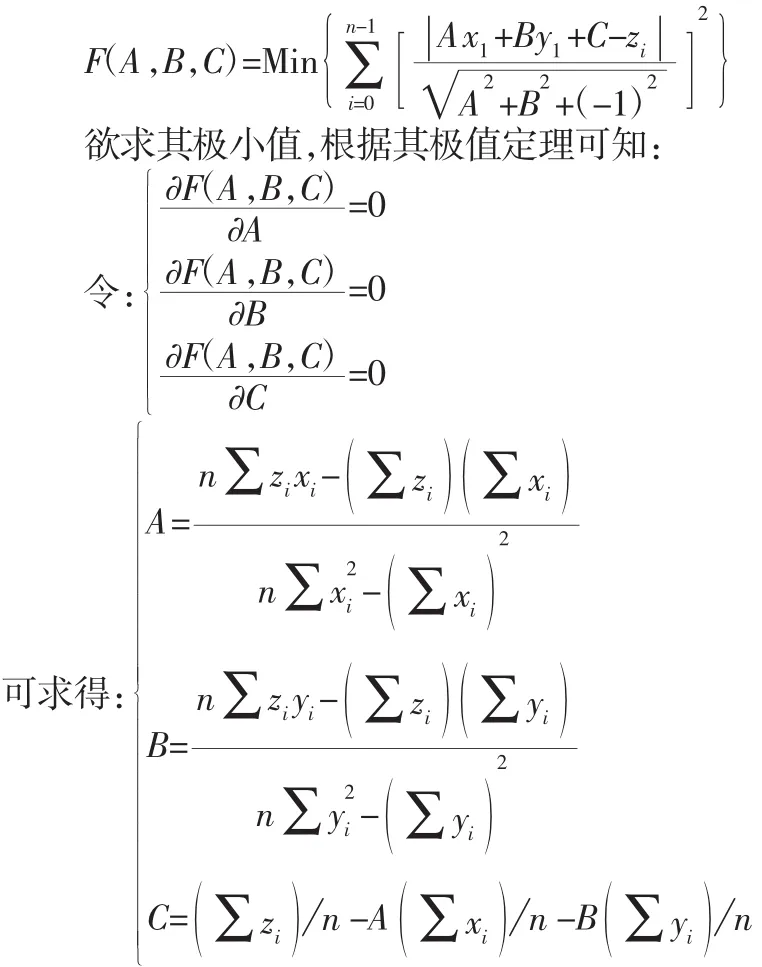
在数据测量的时候，我们难以避免会出现粗大误差，所以在处理数据的时候可能会有粗大误差的数据，此时我们需要将粗大误差的数据剔除，然后用剩下的数据再次求解。

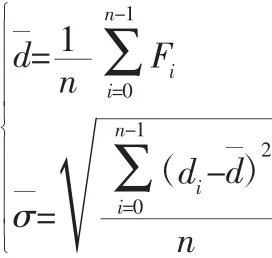
如果Fi>3，则该点是异常点，需作为粗大误差进行剔除，然后用剩下的数据求出A，B，C。通过以上公式可以求出基准平面方程，在此基础上对被测平面进行迭代计算。

3.1.2 用迭代法求解平行度

通过3.1.1中我们求得了基准平面，下面我们需要建立迭代公式来计算出被测平面相对于基准面的平行度，如图8所示。

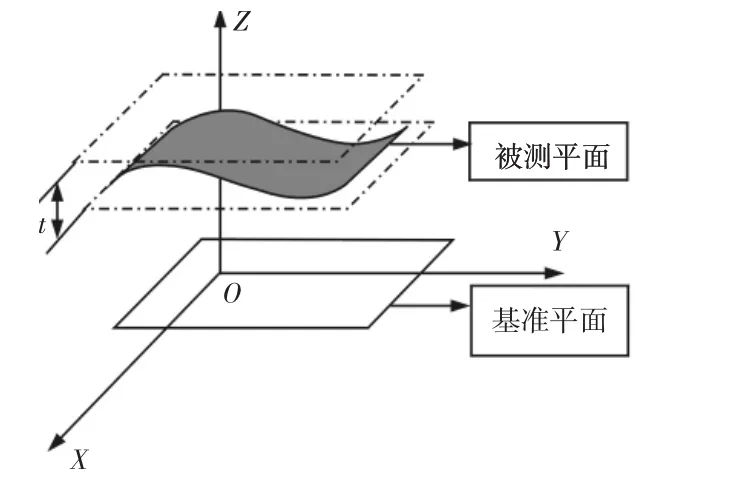
图8 平行度误差示意图Fig.8 Parallelism Error Schematic Diagram

我们需要找到平行于基准平面的两个平面，使其能够全部包括被测平面上的点。平行于基准平面，包括所有点且它们之间的距离最小，此时两平行面之间的距离就是我们所求的平行度误差。要想找到这两个平面，可以通过被测点做一系列平面。找到距离最大两个平行平面，它们之间的距离就是我们所要求的值。

由于通过被测点Ai（xi，yi，zi）的平面平行于基准平面，设通过被测点且平行于基准平面的平面方程为：z=Ax+By+D

点Ai（xi，yi，zi）通过该直线z=Ax+By+D，带入可以求得D的值：

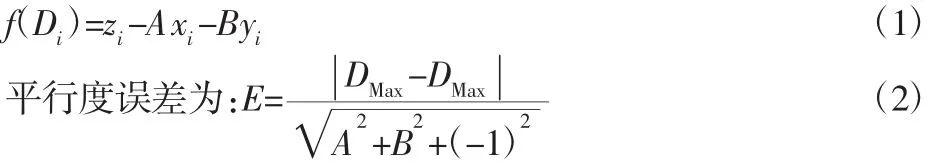
对已知的Ai（xi，yi，zi），首先选取两个点，例如A1、A1可求出D1、D2。比较 D1和 D2，取大值为 Dmax，取小值为 Dmin。

令 D1=DMax，D2=DMin代入公式（2），可求得一个值 E1。

代入 Ai，求得 Di。比较 D1、D2、Di，如果 D3≥D1，则令 Di取代了D1，即Di成了最大值进行下一个数值运算。

如果Di≤D2，则令 Di取代了 D2，即Di成了最小值进行下一个数值运算。

如果 D2≤Di≤D1，则保持 DMax、DMin数值不变，进行下一个数值运算。

以此类推经过计算n个数值的迭代运算我们可以求出最终的DMax、DMin，最后即可求出平行度误差的大小。

3.2 投影迭代法

通过上面的迭代法可以很精确的求出平行度的误差大小但是通过这一方法，当n值很大的时候要经过很多的计算量，计算过程比较复杂。为了解决这个问题，现引入投影法，结合迭代思想组合成投影迭代法这一概念。顾名思义就是为了避免出现三维空间的计算复杂这一情况，我们将三维的平行度投影到一个平面上，使其转变为在二维平面内计算，这样子可以减少计算量、便于计算，并且还可以保持精确性。平行度投影示意图，如图9所示。平行度投影结果图，如图10所示。

图9 平行度投影示意图Fig.9 Parallelism Projection Diagram

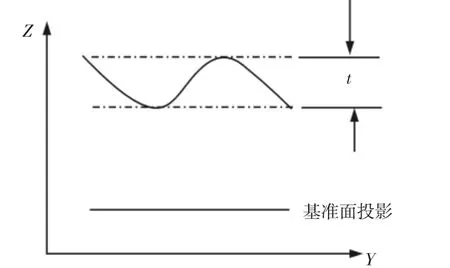
图10 平行度投影结果图Fig.10 Parallel Projection Results

基准平面的求解过程和前面所求的过程一样，在此就不一一叙述，根据以上的内容可以知道基准面的平面方程为：

z=Ax+By+C

基准面到YOZ平面的投影直线为：

点Ai（xi，yi，zi）到YOZ的投影是bj：（yj，zj）；j=0，1，2，，m-1，其中n≥m。

现求平行于z=By+C的两平行线，使其能够平行于该平行直线的两条直线并包括所有点的集合。

欲求这两条直线，同样可以过 bj：（yj，zj）；j=0，1，2，，m-1 做出一些列的平行于基准面投影线的直线，找出距离最远的两直线的即可。

这一系列直线可表述为：zj=Byj+Cj

欲求 CMax、CMin，先给 j以一个初值：C0、C1。比较 C0、C1，例如：若 C0≥C1，令 CMax=C0、CMin=C1。

对其他各个点求出 Cj，比较 CMax、CMin、Cj。

若 Cj≥CMax，则令 CMax=Cj；

若 Cj≤CMin，则令 CMin=Cj；

若 CMin≤Cj≤CMax，则保持 CMax、CMin的数值不变。

以此类推迭代，计算出CMax、CMin的值，最后带入E中求出它的大小即为我们所求的平面度的大小。

4 实例验算

为验证迭代法以及迭代投影法的可行性，特用VB编程对以上算法进行计算分析。本实验采用打表法对实际工件进行测量来获得数据，被测零件放置与以水平平面上，分别沿基准要素和被测要素的X轴每间隔10mm、Y轴每隔20mm测得一个数据，并在每个方向测量3个点，如此测量分别得到基准要素和被测要素各有9个点。根据要求在空间建立坐标系，设定各个点的坐标。如下表所示为所测得的部件所得到的数据，如图11所示。测量数据，如表1所示。用VB编程处理得到的数据，分别用迭代法和投影迭代法处理数据得到平面度误差分别为：59.0532μm和57.0620μm，具体所求得的平面度误差分别，如表2所示。对比迭代法和投影迭代法可知，迭代法和投影迭代法可以准确的求出平面度误差，其中投影迭代法由于它是通过投影法之后再迭代，减少了数据的计算，这样子也减少了数据中可能出现的误差，可以有效地提高精度。

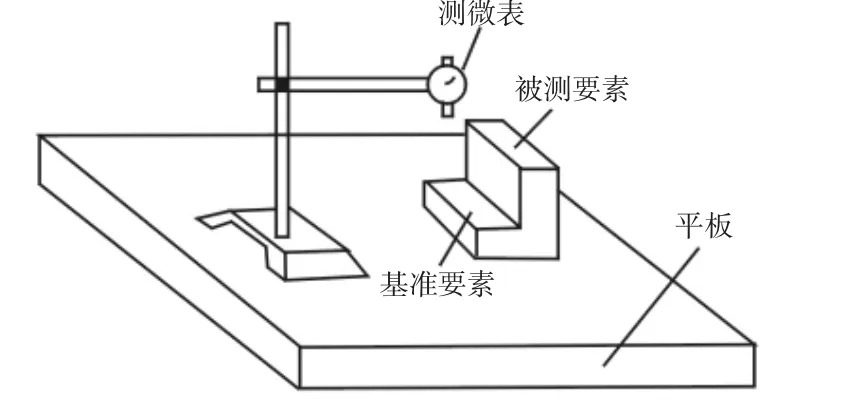
图11 测量示意图Fig.11 Schematic Diagram of Measurement

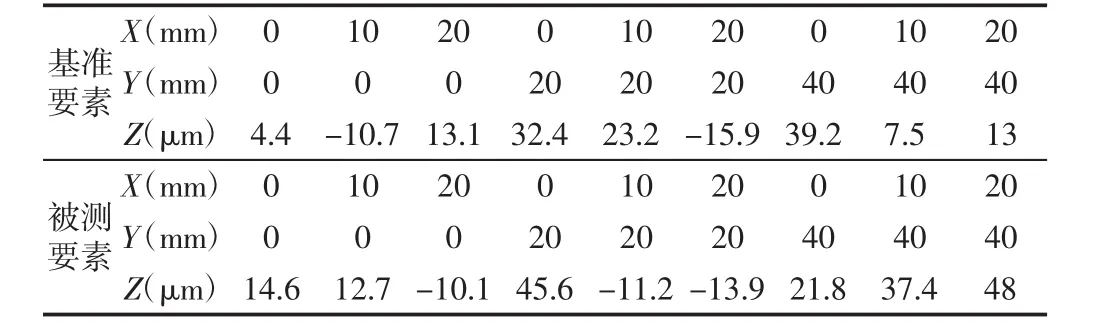
表1 测量数据Tab.1 Measured Data

表2 计算结果Tab.2 Solution Result

5 结论

给出了基于新一代GPS平面度误差检测过程中操作算子的构建过程。同时在此基础上给出了平面度误差求解的一种新方法：迭代法。最后还用迭代法和投影法相结合组成投影迭代法优化了迭代法的求解过程。最后利用实验数据分别用迭代法和投影迭代法求得的平面度大小为59.0532μm和57.0620μm，从而验证了它的正确性。