采用粒子群算法的AGV路径跟踪控制研究

彭慕蓉，肖本贤

（1.合肥工业大学工业与装备技术研究院，安徽 合肥 230009；2.合肥工业大学电气与自动化工程学院，安徽 合肥 230009）

1 引言

近年来，随着自动化智能化技术的提高，自动导引小车（AutomatedGuided Vehicle，AGV）在各个领域得到了广泛应用。例如在仓库和码头等场所，用自动导引叉车代替传统的人工驾驶叉车，不但节约了人力和成本，而且提高了运输效率[1]。常见的导引方式有激光导引，磁带导引[2]等，其中自由路径导引方式，定位精确，路径可变换，灵活性高，能适用各种场合。由于这种导引方式下的指令路径是一条虚拟路径，车辆在行驶中容易受到外界因素干扰而与理想路径之间出现偏差，严重时可能导致车辆偏离航线。当车辆偏离路径时如何快速稳定的回归航线，以及在正常行驶时保持对指定路径的跟踪具有重要的意义。

目前大多数自动导引车辆均采用PID控制策略，PID控制具有控制方法简单易操作的特点，但是PID控制算法依赖于参数的精确性，在复杂情况下参数难以整定，存在适应性差和精确度低等缺点。文献[3]设计了基于线性二次型最的最优控制器，该控制器需要把控制对象简化为线性系统，在控制模型精确的情况下控制精度较高，但在外接干扰情况下鲁棒性较差，稳定度不高。文献[4]采用遗传算法实现了路径跟踪的效果，具有抗干扰强，检测速度快等特点，但遗传算法编程实现比较复杂，计算量大，算法搜索速度慢等缺点。粒子群算法与遗传算法相似，和遗传算法相比[5]，没有交叉和变异等步骤，参数较少，计算速度快，易于实现。

文献[6]采用粒子群算法实现了AGV的路径跟踪，但稳定性差，收敛速度慢，误差较大，没有考虑到粒子迭代过程中搜索能力强弱的问题。文献[7]采用粒子群算法与模糊控制相结合的方法提高了收敛速度，根据时间乘误差绝对值积分准则（Integral time absolute error，ITAE）建立了适应度函数，但忽略了车辆行驶中角度偏差与横向偏差的比例大小，只能在偏差小的情况下消除误差，无法应对各种工况，路径跟踪能力不足。

针对上述问题，建立了AGV行驶全局坐标系和局部坐标系，在简化车辆运动模型的基础上，以消除角度偏差和横向距离偏差为目的，采用粒子群算法设计控制系统。考虑到粒子搜索能力的问题和适应度函数对算法的影响，采用线性递减惯性权重粒子群算法，能在更新过程中改变粒子搜索能力，能有效加强粒子搜索能力，提高收敛速度，设计一种随角度偏差与横向距离偏差所占比重变化而变化的适应度函数，提高车辆回归理想路径的速度和稳定度。

2 AGV路径跟踪系统

研究的AGV共有四个车轮，其中前轮分别由两个电机驱动控制，后轮为万向轮。AGV通过改变速度与方向角即可实现转弯等运动，对于采用差速驱动的AGV，通过调节左右驱动轮的轮速便可实现车辆各种运动方式。

AGV路径跟踪系统结构，如图1所示。该系统包括粒子群算法控制模块，左右轮驱动模块，AGV运动模块。对指定路径进行跟踪，实质是消除小车在行驶过程中与指定路径的角度偏差和横向距离偏差，所以将这两者作为控制系统的输入，将能够驱动电机消除偏差的电压模拟量作为系统输出；经过驱动系统得到AGV的轮速，AGV在轮速调节下向目标路径行驶。

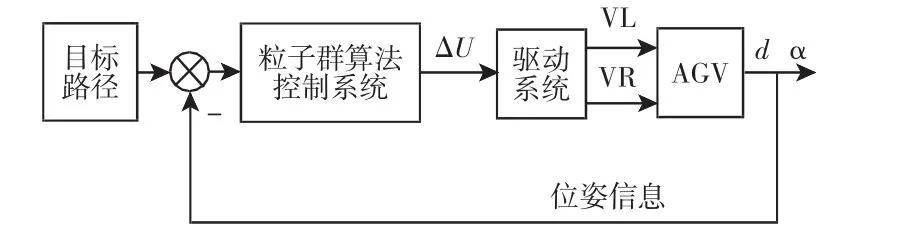
图1 AGV控制系统框图Fig.1 AGV Control System Block Diagram

3 车辆运动系统模型

为了确定AGV的位姿，建立车辆与全局平面之间的联系，简化运动模型，如图2所示。

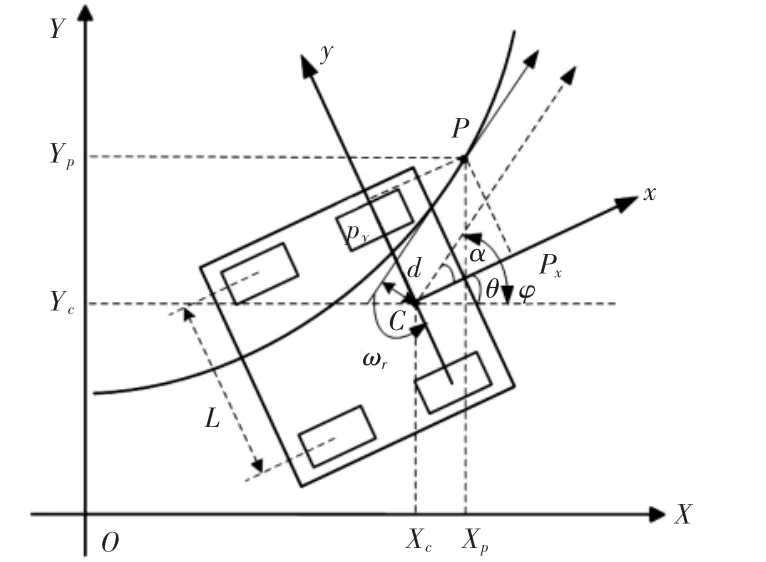
图2 差速驱动AGV简化运动模型Fig.2 Simplified Motion Model of Differential Drive AGV

建立全局坐标系XOY，以车辆中轴线为x轴，驱动轮中点C为原点，建立局部坐标系xCy。车辆在全局坐标系的位姿为（Xc，Yc，θ），图中曲线为跟踪的路径，P（XP，YP）点为车辆跟踪目标点，为x轴与P点切线方向的夹角，d为C点到切线的距离。P点在xCy坐标系中的坐标表示为：

由图2可知，路径跟踪实际上是车辆追赶目标点的过程，就是是要消除与目标点之间的角度偏差α与横向距离偏差d。在坐标系xCy中分析AGV行驶偏差，根据车辆结构和运动学可知：

式中：L—左右轮距；ωr—车辆角速度；VL和VR—左右驱动轮速度。

经过时间Δt，车辆的角度改变量Δα和横向距离偏差改变量Δd为：

设两驱动轮速度差为ΔV，得到：

要实现车辆自动行驶，还应知道AGV驱动模块如何运转，并建立能反映系统驱动特性的模型，但AGV驱动环节较多，各部件的性能参数难以确定，所以难以用解析法推导出其数学模型。采用系统辨识的方法，即通过测量系统输入输出量，根据相应规则，估算出能反映系统属性的数学模型。现引入控制速度的纠偏电压ΔU作为辨识系统的输入，根据文献[8]，选择调整时间和周期信号，采用最小二乘法进行系统辨识，通过Matlab软件编程并进行降阶处理后得到传递函。

微分方程为：

式中：ΔV—纠偏速度。

将电压模拟量作为输入量，驱动轮速度做状态变量，输出为角度偏差和横向距离偏差，车辆控制框图，如图3所示。

图3 运动控制系统框图Fig.3 Motion Control System Block Diagram

整个系统状态方程为：

4 改进粒子群算法优化的控制系统

现阶段对车辆行驶稳定性，安全性，快速响应提出了更高的要求，用传统的控制方法进行轨迹跟踪，往往具有较大的误差，无法满足性能要求，粒子群算法（Particle Swarm Optimization）是一种基于种群的智能优化算法[9]，具有快速收敛，计算简单，精度高等优点，应用于轨迹跟踪时能快速有效的达到减小误差的目的。

4.1 改进的粒子群位置更新方法

AGV行驶环境复杂，稳定性要求高，在轨迹跟踪中需要有快速响应的性能。基本粒子群算法中的粒子更新时，其惯性权重系数ω是一个常数，在面对复杂问题时，后期容易陷入局部极值，无法满足快速收敛的要求，采用线性递减的惯性权重系数对上述缺点进行改进。惯性权重ω是粒子群算法中的重要参数，可以用来控制算法的探索能力。有研究表明，较大的ω能有效提高全局搜索能力，增加种群多样性，能够跳出局部极值，较小的ω能提高算法的局部搜索能力，加快收敛速度。线性递减的惯性权重系数，根据种群更新次数对ω进行动态调节，在算法前期ω取较大值，确保种群粒子更加丰富，搜索区域更加广泛，随着迭代次数增加，逐渐减小ω值，使算法后期具有较强局部搜索能力，能够快速的找到最优解。

式中：ωmax—最大惯性权重；ωmin—最小惯性权重；Tmax—种群最大更新次数；t—当前种群更新次数。

设计的路径跟踪粒子群控制方案中，求解问题为消除行驶偏差，问题的解为能够驱动左右轮消除偏差的电压。将问题的解集抽象为一个种群［x1，x2，…，xm］，种群中的每个粒子代表一组电压值。每个粒子的位置用矢量 xi=（xi1，xi2，…，xiD）表示，每个粒子的速度用矢量 vi=（vi1，vi2，…，viD）表示。粒子 i到目前经历的最好位置为 pbesti=（pbesti1，pbesti2，…，pbestiD），种群目前搜索到的最优位置为 gbest=（gbest1，gbest2，…，gbestD）。粒子的速度和位置更新公式如下：

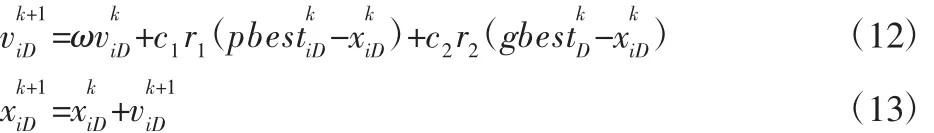
式中：i=1，2，…，m；ω—惯性权重；c1和 c2—学习因子；r1和 r2—［0，1］之间的随机数；D—粒子的维数；k—当前迭代次数。

4.2 适应度函数的建立

为了判断粒子每次迭代后的位置优劣，需要一个评判标准，故建立适应度函数。由于ITAE准则[10]设计的系统具有超调量小，动态性能好等特点，所以采用角度偏差和横向距离偏差的ITAE之和作为目标函数。

式中：ω1和ω2—比例系数，决定角度偏差和距离偏差在控制过程中所占的比重；α（t）和 d（t）—t时刻的航向偏差和距离偏差。

在车辆行驶过程中，横向偏差和航向角度偏差不断地发生变化，常规的适应度函数中两种偏差采用固定比重，这种调节方式无法适应各种工况，针对这一问题，对目标函数进行改进，设计一种根据两种行驶偏差实时改变比重系数的动态目标函数。在t时刻车辆的横向偏差为dt，角度偏差为αt，车辆行驶允许的横向偏差和角度偏差为 αC和αC，设 k1=dt/dC，k2=αt/αC，分别表示 t时刻的位置偏差dt和αt角度偏差与允许的位置偏差与角度偏差的比，则该时刻的目标函数中加权系数为：

由于f反应的是车辆与理想路径的偏差，所以f越小，则说明该粒子越优。

5 系统仿真及结果

为了验证上文提出的改进粒子群算法对路径跟踪的纠偏效果，在Matlab/simulink模块进行仿真实验。选取粒子种群规模m=30，粒子最大迭代次数T=100，学习因子C1=C2=2，车辆轮距L=1.8m，车辆行驶速度为1m/s。首先进行惯性权重对算法的影响对比，车辆与理想路径的初始角度偏差为10°，初始横向偏差距离为10cm。设标准粒子群算法的惯性权重系数为ω=0.9，改进后惯性权重最大值为ωmax=0.9，惯性权重最小值为ωmin=0.4，在不同的惯性权重影响下，目标函数的适应度值变化曲线，如图4所示。

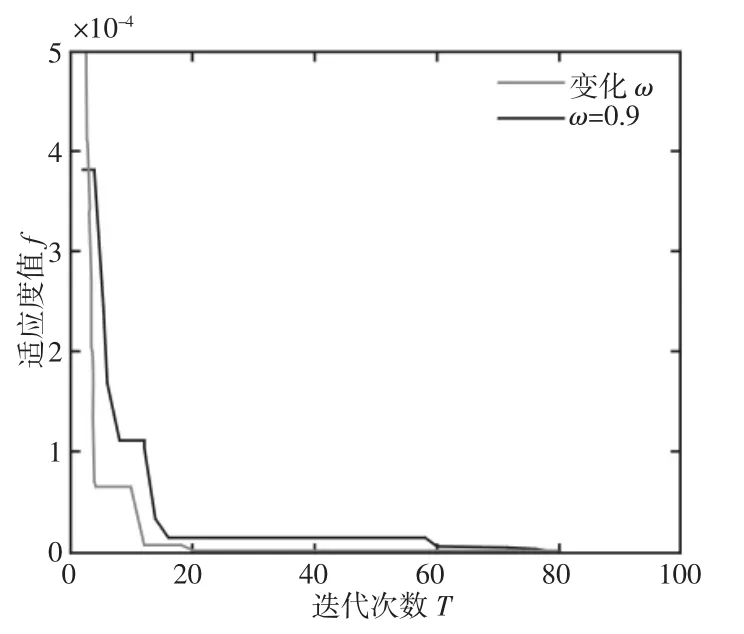
图4 适应度值曲线Fig.4 Fitness Curve

图中：ω=0.9的情况下，种群迭代第17次开始，适应度值长时间没有变化，随着迭代次数的增加，迟迟不能跳出局部极值，直到迭代第60次时才摆脱这个困境而收敛。在ω随迭代次数线性变化的情况下，种群迭代至20次时收敛，大大减少了种群迭代次数。仿真结果表明，变化的惯性权重系数可以提高粒子的搜索能力，防止粒子陷入早熟。其次在上文的基础上，对采用固定适应度函数和改进适应度函数时，车辆消除横向偏差与航向偏差的能力进行仿真实验。设适应度函数比重系数ω1=0.7，ω2=0.3。车辆与理想路径的初始偏差为［10°，10cm］。两种适应度函数下车辆行驶横向距离偏差与角度偏差仿真图形，如图5所示。

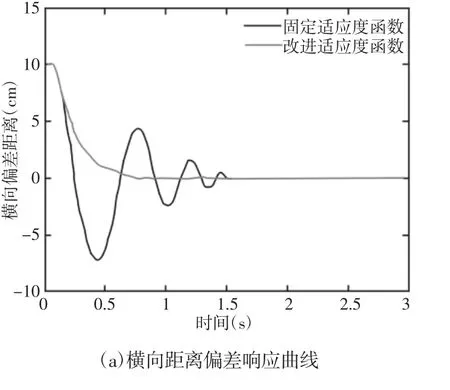
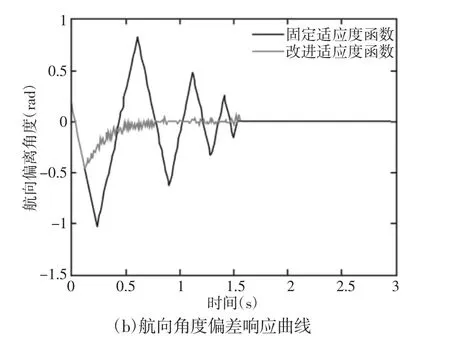
图5 距离偏差与航向偏差响应曲线Fig.5 Distance Deviation and Angle Deviation Response Curve

图5 （a）显示，在固定适应度函数调节下，横向偏差在［-7.2cm，10.4cm］范围内变化，车辆在回归航线的过程中出现了多次过度行驶，这使车辆在指定路径两侧进行反复调节，增加了车辆行驶路程，产生较大波动，消除横向偏差总共需要1.51s。在改进适应度函数后，横向偏差在［0cm，10.4cm］范围内变化，车辆消除横向偏差总共需要0.8s。虽然两种控制方法最终都达到了路径跟踪的目的，但是后者收敛时间更短，超调小，稳定性高，具有更好的响应特性。

图5（b）反映了车辆回归期望路径过程中航向角的变化情况，在固定适应度函数调节下，车辆的航向角在［-1rad，0.85rad］范围内变化，航向经历了9次左偏和右偏的改变，最大改变量为1.85rad，这会导致车辆左右摆动，行驶稳定性差，增加不安全的因素。在改进适应度函数后，航向角在［-0.47rad，0.17rad］范围内变化，并保持航向基本左偏，跟前者相比，具有调节时间短，收敛速度快，精度高的优点，保证车辆安全稳定行驶。

最后对AGV跟踪路径过程进行模拟，建立环境坐标系XOY，设理想路径为一条直线，车辆行驶起点为（0，0），现在以初始偏差为［10cm，10°］，车速1m/s跟踪理想路径，仿真结果，如图6所示。

将标准粒子群算法调节下和改进粒子群算法调节下AGV消除偏差的能力进行对比，通过改进的控制方案能够快速且稳定的消除行驶中的误差，具有较强的路径跟踪能力。

图6 模拟轨迹跟踪路径图Fig.6 Simulated Path Tracking Diagram

6 结论

对双轮驱动差速控制的AGV路径跟踪问题进行研究，基于横向偏差和航向偏差两者与速度关系建立运动模型，采用线性递减惯性权重系数对粒子群算法进行改进，并结合AGV运动特点，提出变化的适应度函数调节策略。仿真结果表明，采用粒子速度更新公式中惯性权重系数线性递减的方法，可以提高粒子搜索速度，避免陷入局部极值；采用随横向偏差和航向偏差动态变化的适应度函数调节方法，与固定比例系数适应度函数调节方法相比，调节时间段，超调量小，车辆行驶更加稳定，安全，对路径的跟踪能力更强。