淬硬钢模具型腔铣削稳定性分析

姜彦翠，仇 焱，刘献礼，崔 健

（哈尔滨理工大学机械动力工程学院，黑龙江 哈尔滨 150080）

1 引言

淬硬钢模具的加工和生产是机械制造业的重要环节，淬硬钢模具型腔形状复杂多变，在模具型腔刀具路径曲线曲率变化处的铣削加工过程中，动态切削厚度的大幅波动极易导致加工颤振的产生[1]，使得工件表面在加工过程中产生振纹，表面的粗糙度变高，影响加工精度，甚至可能会损坏刀具和机床，因此对淬硬钢型腔模具铣削加工过程中颤振的抑制，保证铣削过程的稳定性是十分必要的[2-4]。目前关于铣削稳定性和铣削动力学的研究主要针对平面铣削过程，对于型腔曲线的铣削过程动力学已有一部分学者进行了研究。文献[5]建立了圆弧铣削颤振稳定性的频域模型和数值模型。文献[6]针对型腔工件结合给定刀具路径的材料去除几何信息，提出一种基于频域的的铣削稳定性频域求解方法。文献[7]建立圆角铣削动力学模型，主要以直线铣削过程为基础，建立圆角铣削动力学模型。文献[8]是基于直线插补给出了刀具位置角、进给方向角的确定方法，考虑了刀具偏心跳动对切削厚度的影响，建立了变曲率曲线铣削动力学模型。文献[9]考虑模具拐角处铣削加工切削厚度的变化，建立拐角处的瞬时铣削力模型。以上研究主要针对工件圆角的铣削加工过程，重点研究圆角铣削的切削厚度和刀具工件切触区域，建立铣削力模型和铣削动力学模型[10]。

针对淬硬钢模具型腔曲线路径进行铣削动力学建模和铣削稳定性分析，建立模具型腔加工过程中的未变形动态切削厚度以及刀具-工件接触区域修正模型，引入到铣削动力学模型中，运用全离散法进行铣削稳定性分析，获得模具型腔特征参数和铣削工艺参数对铣削稳定性的影响规律。

2 铣削动力学建模

当刀具铣削淬硬钢模具型腔时，如图1所示。刀具的刚性远小于淬硬钢模具工件的刚性，刀具系统为柔性，铣刀及约束简化成弹簧阻尼系统，并建立以铣刀中心作为原点的全局坐标系，如图2所示。在实际铣削情况中，切削厚度并非一个定值，而是动态变化的。模具型腔曲线路径的铣削可以简化为2自由度振动系统，动态切削厚度可以表示为静态切削厚度与相邻两刀齿由于振动引起的瞬时动态切削厚度的和，即：式中：h（t）—指切削厚度；hNj（t）—指静态切削厚度；uj、uj0—指刀具在前后两个刀齿周期与工件接触点的位置；g（φj（t））—指判断刀齿是否处于切削区的单位阶跃函数。

静态未变形切削厚度：

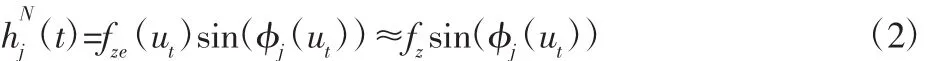
式中：ut—t时刻刀具中心位置对应的参数化曲线参数；fze（ut）—刀具中心位于ut时实际每齿进给量；φj（ut）—指切削微元在坐标系中的位置角。瞬时动态切削厚度：

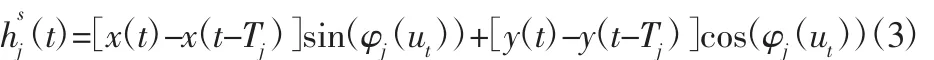
式中：（x（t），y（t））—t时的振动位移相应；Tj—再生时滞。

图1 模具型腔铣削实例Fig.1 An Example of Mold Cavity Milling

图2 动态铣削过程动力学模型Fig.2 Dynamic Milling Process Dynamics Model

因为该系统的动态响应以刀具的模态为主，Z方向的模态与X、Y两个方向的相差较大，故暂时忽略，则该系统在X、Y两个方向上铣削动力学模型表达式为：

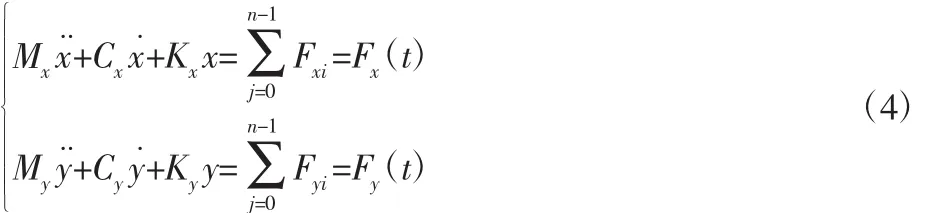
式中：Mx、My、Cx、Cy、Kx、Ky—系统在 X、Y 方向上的模态质量、模态阻尼和模态刚度。

基于线性切削力模型，若不考虑螺旋角，设轴向切削深度为ap，则作用在第j个刀齿上的切向力和径向力，与hj（t）存在着线性关系如下所示：

式中：Kt、Kr—切向铣削力系数和径向铣削力系数；g（φj（t））—一个阶跃函数如下：

式中：φst、φex—刀具的径向切入角和径向切出角，并且受到径向切削深度ae和铣削方式的影响。

将式（5）中的径向力和切向力变换成在旋转坐标系的X、Y方向的铣削力合力的大小，则：

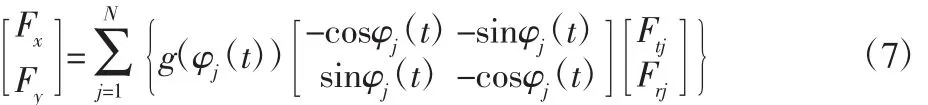
3 未变形动态切厚计算

未变形动态切屑厚度的计算可以通过等效进给量、微元在随动坐标系中的位置角进行计算。实际每齿进给量示意图，如图3所示。在图3中，当刀具运行到B点时，该点的切线方向即为刀具进给方向，图中：DE—实际每齿进给量。

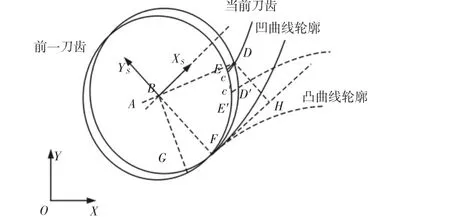
图3 实际每齿进给量示意图Fig.3 Diagram of Actual Feed Per Tooth

利用图3中的几何关系，列出D、E（xe、ye）的坐标求解方程组点坐标可以通过下式求解：

式中：（x（tu），y（tu））、（xω（u），yω（u））—加工前轮廓曲线和刀具路径曲线；则，刀具中心位于B点时实际每齿进给量fz（eu）b：

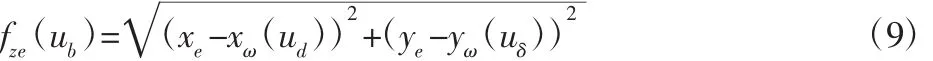
当刀具中心位置对应参数u时，微元（i，j）的瞬时未变形切削厚度为：

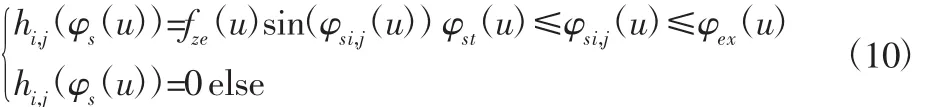
式中：φst（u）、φex（u）—刀具位于参数u时在坐标系中的瞬时切入角和切出角。

4 刀具-工件接触区域确定

在模具型腔曲线路径铣削过程中，曲率的变化使得径向切深不断变化，刀具位于不同位置和在不同曲率曲线路径时具有不同的径向切深。径向切削深度直接影响刀具-工件接触区域，即切入角和切出角。

图3中DH即为刀具位于B点时的实际径向切深，根据点到直线距离的计算公式，刀具位于B点的实际径向切深为：

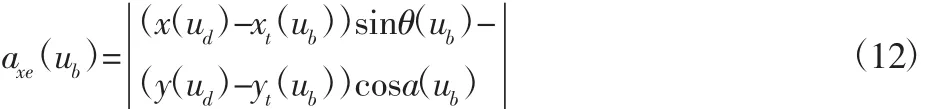
式中：axe（ub）—刀具位于B点时的实际径向切深。

由实际径向切深可计算出切入角与切出角为：

5 模具型腔铣削稳定性影响分析

将以上针对模具型腔铣削时的未变形动态切厚和刀具-工件接触区域的修正形式引入到铣削动力学模型，即式（4）中，应用全离散法，进行模具型腔曲线铣削稳定性预测，具体运算步骤见文献[11-12]。选择径向切深ae=4mm为时，主轴转速选择范围是（3000～7000）r/min，每齿进给量 fz=0.025mm/r时，选择模具型腔曲线曲率半径R分别为400mm、500mm、600mm进行仿真，如图4所示。可以看出模具型腔曲线路径曲率半径的变化影响铣削颤振稳定极限曲线上下位置的变化，左右位置的变化并不明显，即影响极限轴向铣削深度。随着模具型腔曲线路径曲率半径的降低，极限轴向铣削深度逐渐增加。选择径向切深为ae=4mm时，主轴转速n选择范围是（3000～7000）r/min，每齿进给量 fz=0.025mm/r时，选择两直线间夹角分别为 30°、60°、120°进行仿真计算，如图5所示。能够看出模具型腔曲线路径拐角处角度的变化使得铣削稳定极限曲线左右移动，上下移动并不明显，即随着模具型腔曲线路径拐角角度的增加，铣削稳定性变差。

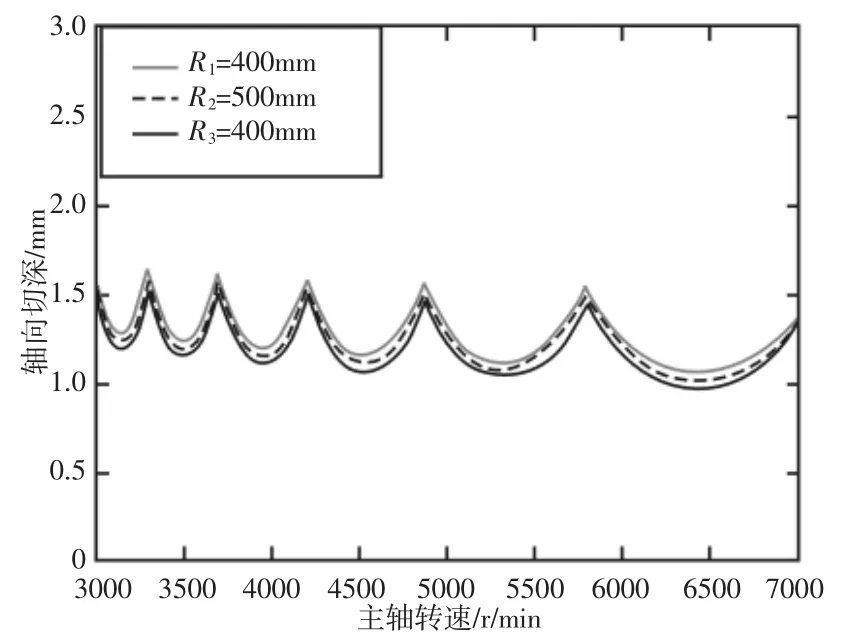
图4 模具型腔曲线曲率半径R对铣削稳定性的影响Fig.4 Effect of Curvature Radius of Die Cavity Curve on Milling Stability

图5 模具型腔拐角角度对铣削稳定性的影响Fig.5 Effect of Corner Angle of Die Cavity on Milling Stability

选择每齿进给量为fz=0.02mm/r，对径向切深（ae=0.5mm、1.5mm、3mm、4mm）进行仿真计算结果，如图6所示。可以看出，随径向切深的增大相同转速时临界轴向切深减小曲线下移，铣削稳定性减弱。

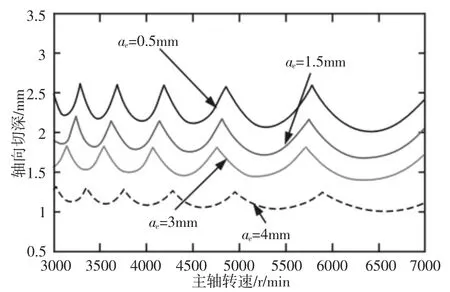
图6 径向切深对稳定性的影响Fig.6 The Influence of Radial Depth of Cut on Stability

在径向切深为ae=4mm时，改变刀齿数（N=2、3、4）进行仿真计算结果，如图7所示。可以看出，随铣刀刀齿数增加稳定性极限图左移，即临界轴向切深减少，铣削稳定性变差。由此可以看出铣削稳定性与刀齿数成反比。

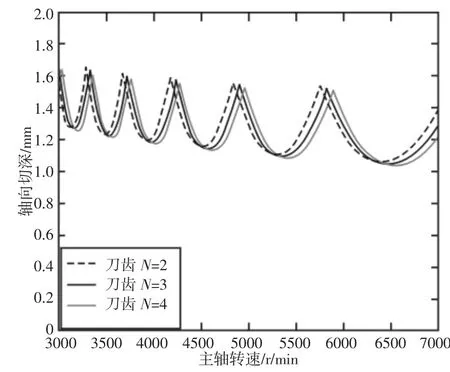
图7 铣刀齿数对颤振稳定性的影响Fig.7 The Influence of Milling Cutter Tooth Number on Flutter Stability

6 结论

（1）针对淬硬钢模具型腔曲线路径铣削过程，对未变形动态切削厚度、实际径向切深和切入、切出角进行修正，建立模具型腔曲线铣削动力学模型，并运用全离散法进行淬硬钢模具型腔曲线铣削稳定性预测。

（2）分析模具型腔形状特征参数对铣削稳定性的影响，模具型腔曲线路径曲率半径的变化影响铣削颤振稳定极限曲线上下位置的变化，左右位置的变化并不明显，即影响极限轴向铣削深度。随着模具型腔曲线路径曲率半径的降低，极限轴向铣削深度逐渐增加。模具型腔曲线路径拐角角度变化使铣削稳定极限曲线左右移动，上下移动并不明显，即随着拐角角度的增加，铣削稳定性变差。

（3）分析铣削工艺参数对淬硬钢模具型腔铣削稳定性的影响，随着径向切削深度的降低，极限轴向铣削深度逐渐增加[12]，铣削稳定性变好；随着铣刀刀齿数的增加，稳定性图形左移，极限轴向切深相对较小，铣削稳定性变差。