利用GS优化SM-SVM的滚动轴承故障诊断方法研究

周 超，曹春平，孙 宇

（南京理工大学机械工程学院，江苏 南京 210094）

1 引言

滚动轴承作为标准件，被广泛应用在众多机械设备中，也是机械设备中极容易损坏的零部件。据统计，在使用滚动轴承的旋转机械中，大约有三成的机械故障都是由轴承引起的[1]。轴承状态是否良好对机械设备工作性能有较大的影响[2]。处于故障状态时，滚动轴承转动会产生较大的振动和噪声，因此可以采用振动检测的方法来诊断轴承故障。滚动轴承故障模式识别一直是机械故障研究的热点之一[3]。

滚动轴承常见故障包括外圈故障、滚动体故障、保持架故障和内圈故障。当这些故障出现时，滚动轴承振动信号的时域统计量，如峭度指标、偏度系数和方均根值等，会有较大的波动和变化，同时信号的小波包分解节点能量分布不同。故可利用上述特征可以对滚动轴承的故障进行识别诊断和分类。

故障模式识别常用的方法有神经网络识别法、粗糙集识别法、模糊理论识别法和支持向量机（SVM）识别法等[4]。文献[5-7]于上世纪九十年代首先提出了支持向量机的机器学习方法，它在解决非线性、小样本及高维度模式识别问题中具有独特的优势，被广泛的应用于机械设备的故障诊断。文献[8]针对乘用电梯常见故障提出利用遗传算法优化最小二乘支持向量机（LS-SVM）的故障模式识别和诊断方法。文献[9]提出基于多层相关向量机分类器（Mulit-Layer RVM Classifier）的故障模式识别方法，并对电动机轴承故障进行诊断。文献[10]采用将瞬时能量熵和SVM相结合的方法进行滚动轴承故障诊断。文献[11]利用人工免疫算法优化支持向量机以进行电力变压器的故障诊断。文献[12]采用迁移学习和改进LS-SVM相结合的方法来诊断滚动轴承故障。

上述方法用于故障诊断时，存在对高维度大样本训练耗时多、模式识别正确率低、可能得不到全局最优解的缺点。因此，将网格搜索算法引入到序列最小支持向量机，通过GS算法对SMSVM的关键参数进行优化，利用优化后的方法对滚动轴承的故障进行识别和诊断，以提高故障识别的正确率和速度。最后将本方法与SM-SVM和LS-SVM方法进行了比较，结果表明，所提出方法能有效诊断滚动轴承故障并可提高滚动轴承故障模式识别正确率。

2 序列最小支持向量机

2.1 序列最小支持向量机

2.1.1 基本原理

在二值支持向量机中，设｛xi，yj｝为样本集，i、j∈｛1，2，3，…，n｝，n 是样本数，xi=（q1，q2，…qp）∈Rp是 p 维故障特征向量（数据点），yj∈｛-1，1｝是分类标签，则分类超平面可表示为：

式中：ω=（ω1，ω2，…，ωp）—权重系数；b—常数。

支持向量机分类时，依据所选的分类超平面使得样本各类之间的几何间隔最大化条件，并考虑到离群数据点对超平面建立的影响，构建如下目标函数：

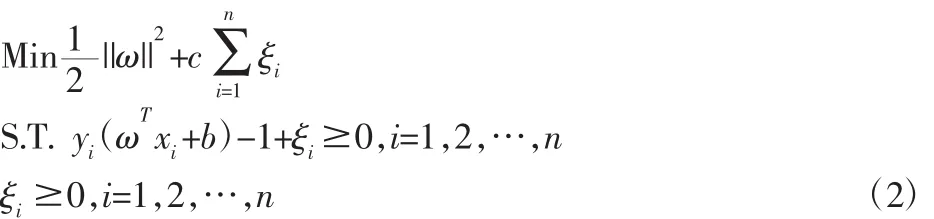
式中：ξi—松弛变量，该变量允许数据点偏移；c—惩罚因子，表示对误差的容忍度，该变量对目标函数的权重系数和松弛变量起控制作用。

利用拉格朗日乘子法，并考虑到KKT（Karush-Kuhn-Tucker）条件（非线性规划问题有最优解法的充要条件）将目标函数（2）变换成：

式中：αi、αj—拉格朗日乘子系数；

K（xi，xj）—核函数。

序列最小支持向量机在模式识别时，利用序列最小算法在拉格朗日乘子系数｛αi｝i=｛1，2，3，…，n｝上求解目标函数（3）。求αi，每次从乘子系数中任取两个，如αr和αs，并固定剩余的乘子系数，使得目标函数只与所取两个乘子系数有关。如此反复抽取，迭代求解子问题，最终目标函数得以求解。

2.1.2 核函数和分类策略选取

（1）SVM核函数

利用SVM对数据点类别预测时，若样本线性不可分，则需将低维数据点通过函数映射至高维空间，从而实现样本线性可分[14-15]。采用核函数可将低维数据点映射到高维空间，SVM常用的核函数有线性核（Linear Kernel）、多项式核（Polynomial Kernel）、高斯核（Radial Basic Function）和S核（Sigmoid Kernel）。其中高斯核是一种局部性强的核函数，能把样本点映射到更高维空间内。该核函数应用非常广，无论样本大小均有比较好的性能，而且其相对于多项式核函数的参数少，故选择高斯核函数，函数如下：

式中：γ（gamma）—可优化的核函数参数g，该参数对决定分类超平面的支持向量有重要影响。

（2）SVM分类策略选择

SVM本为二值分类器（Binary-Class Support Vector Machine，BSVM），对于多分类问题需将BSVM组合成多分类器（Multi-Class Support Vector Machines，MSVM）以实现多分类。常见的SVM多分类策略有一对一（o-v-o）、一对余（o-v-r）、DAG（有向无环图）和决策树等。进行K分类时，一对一分类策略需要K（K-1）/2个BSVM，有重叠分类，不存在不可分的情况。采用一对一的分类策略。

2.2 网格搜索法

网格搜索法是常用的参数优化方法，本方法用于模型参数寻优的基本思路为：将需要优化的参数在选定的空间内进行网格划分，通过遍历所有网格节点，即可获得使模型性能最佳的参数值（节点）。该算法具有简单方便、寻优速度快且不会陷入局部最优的特点，广泛用于支持向量机参数的寻优[15]。此算法参数寻优具体步骤如下：

（1）确定参数范围，在参数的空间中划分网格并形成网格节点Ni；

（2）选择合适的网格搜索步长，一般可选0.5，精细搜索可选0.1；

（3）计算每一网格节点Ni下的目标函数值并作图表示；

（4）若所有网格节点已搜索完毕，转到（5）；若所有网格节点搜索未完成，转到（2）；

（5）输出最优参数No。

3 基于GS优化SM-SVM的故障识别

GS优化SM-SVM的模式识别，如图1所示。首先，采集滚动轴承不同故障状态的振动信号并对信号进行预处理；然后，对预处理后的信号提取不同特征并将提取特征融合以构成特征向量（样本点）；其次，将样本点按一定比例分为训练集Tr和测试集Te，并把Tr送入SM-SVM，同时对GS算法和训练SM-SVM进行模型参数设置，包括核函数参数g、惩罚因子c、搜索步长g/cstep、K折交叉验证折数v、数据点归一化范围φ、PCA降维主成分Pca等；再次，利用Tr训练SM-SVM，计算不同网格节点（gi，ci）下的模式识别正确率ai，通过比较不同的（gi，ci，ai）以获得GS优化的参数（go，co）和最佳适应度VCAccracy，此时训练完毕的 SM-SVM即为测试SM-SVM；最后，将Te送入测试SM-SVM中进行模式识别并获得分类结果。

图1 GS优化SM-SVM的模式识别模型Fig.1 The Model of Pattern Recognition Using SM-SVM Optimized with GS Method

4 滚动轴承故障模式识别

4.1 振动信号数据获取

利用故障模拟试验台来采集滚动轴承的振动信号。实验中，首先，利用电火花分别在三只规格相同轴承的外圈、滚动体、内圈以某一直径加工出故障点；其次，将不同故障状态（包括轴承正常状态）的滚动轴承依次安装在电动机轴承座上，并设定电动机转速，施加载荷，启动电动机；最后，设置信号采集频率、电荷发放大系数等参数并将磁座加速度传感器吸附在轴承座上以采集不同故障状态下的滚动轴承振动信号。实验条件，如表1所示。对滚动轴承的四种故障状态，从中各截取30段振动数据，每段512点，利用所截取的数据提取故障特征。

表1 振动信号采集实验条件Tab.1 Experimental Conditions of Vibration Signal Acquisition

4.2 信号预处理

从现场采集的振动信号均含有环境噪声和干扰项，为提高信噪比，对原始信号进行预处理。五点三次平滑法可去除信号的高频噪声干扰，使得信号曲线变得光滑且信噪比提高；最小二乘法可去除信号中的趋势项以减弱信号的失真。采用上述方法对振动信号进行预处理，滚动轴承正常状态的原始和预处理振动信号，如图2所示。

图2 滚动轴承原始振动信号和预处理振动信号Fig.2 The Original Vibration Signals and Pre-Processed Vibration Signals of Rolling Bearing

4.3 特征提取

4.3.1 时域特征提取

时域统计量峭度指标对设备零部件早期特别故障敏感，零件故障时该指标将大于三；偏度系数在零部件故障时，其分布函数将偏离中心，不再对称。有效值（均方根值）能较好地反映振动信号的能量、稳定性、重复性，当该值超出允许范围较大时，表明出现故障。将对预处理后的信号分别提取峭度指标、偏度系数、方均根值、裕度指标和波形指标五项时域统计量Tds。

4.3.2 时频域特征提取

反映滚动轴承故障特性的特征向量的维数不能过少，否则特征向量不足以表征某类故障状态，且利用低维特征向量进行模式识别的正确率一般较低。

仅时域特征不足以反映滚动轴承故障的真实特性，还需要结合时频域特征。当滚动轴承出现不同故障时，其振动信号的小波包分解节点能量分布不同，利用该特征能够对故障进行识别分类。振动信号小波包分解节点能量提取流程，如图3所示。

图3 信号小波包分解节点能量提取流程Fig.3 The Flow Chart of Extraction Node Energy of Signal Wavelet Packet Decomposition

图中：S3j—信号小波包分解树第三层节点的重构信号，j=｛0、1、2、…、7｝；Ej—S3j对应的能量，E=［E0，…，E7］/E*，E*—重构信号S的总能量；E—信号小波包分解节点能量向量；db3小波基适合振动信号特征的提取。

将振动信号的时域统计量Tds，包括峭度指标Kur、偏度系数Ske、裕度指标 Mar、有效值 Rms、脉冲指标 Si，和时频域特征小波包分解节点能量向量E融合，则模式识别特征向量［Tds，E］可表示为［Kur，Ske，Mar，Rms，Si，E］。

4.4 SM-SVM参数优化

图4 GS优化参数图Fig.4 Parameter Map of GS Optimization

GS对SM-SVM参数寻优步骤为：（1）确定参数g和c的范围，并在g和c的空间中划分网格以形成网格节点（gi，ci）；（2）选择合适的网格搜索步长；（3）计算每一网格节点（gi，ci）下的K折交叉验证模式识别正确率ai，并作图表示（gi，ci，ai）；（4）若所有网格节点已搜索完毕，转到（5）；若所有网格节点搜索未完成，转到（2）；（5）输出最优参数（核函数参数、惩罚因子和模式识别正确率（go，co，ao））。模型参数设置，取核函数参数g和惩罚因子c均在［2-8，28］、核函数参数搜索步长gstep和惩罚因子搜索步长cstep为0.5、K折交叉验证折数v为10、数据归一化处理的范围φ为［-1，1］、特征向量PCA降维处理的主成分Pca为98%。取K折交叉验证的分类正确率作为适应度函数值CVAccuracy。利用MATLAB LIBSVM计算，获得最佳适应度CVAccuracy为93.75%，最优参数（go，co）为（0.088，4），GS优化参数，如图4 所示。

4.5 故障识别分类

取滚动轴承正常（Nor）、内圈故障（Inn）、滚动体故障（Bal）和外圈故障（Out）四种状态的样本（特征向量）各30个，共120个。其中，训练集Tr100个样本；测试集Te20个样本。SVM的输入样本参数及故障标签，如表2所示。三种SVM的滚动轴承故障模式识别正确率，Atr、Ate、Aal分别是训练集、测试集和总集（测试集和训练集）的模式识别正确率，其中，Aal是总集用于训练后的测试模式识别正确率，如表3所示。从表3可以看出，经过GS优化SM-SVM的滚动轴承故障模式识别正确率从训练集、测试集或者总集来说，均高于未进行参数优化的SM-SVM，前者的平均分类正确率比后者高出3.8%，分类结果，如图5所示。从图5可以看出，滚动轴承的正常状态（1）、内圈故障（2）和滚动体故障（3）均被完全正确地识别归类，而滚动轴承外圈（4）故障的两个样本被误分至内圈故障。这可能是因为滚动轴承内外圈故障类似，提取特征量的大小也接近，从而导致GSSM-SVM类别误分。可以寻找对滚动轴承故障更为敏感的特征以进一步提高滚动轴承的故障模式识别正确率。

表2 SVM输入样本参数Tab.2 Enter the Sample Parameters of SVM

表3 三种SVM的滚动轴承故障模式识别正确率Tab.3 Fault Pattern Recognition Accuracy of Three Types of SVM for Rolling Bearing

图5 GS SM-SVM测试分类结果Fig.5 Test Classification Results of GS SM-SVM

5 结论

针对一般方法在滚动轴承故障模式识别中分类正确率低、可能得不到全局最优解的缺点提出了利用GS优化SM-SVM的滚动轴承故障诊断方法。将提出的方法与LS-SVM和未优化的SM-SVM在滚动轴承故障模式识别正确率上进行了比较，结果表明，所提出的方法可以有效诊断滚动轴承故障且能够提高故障模式识别正确率。