关于高中数学建模教学的实践
2020-06-18林玉萍
林玉萍
(福建省莆田锦江中学 351115)
高中数学涉及很多模型,如函数模型、不等式模型、数列模型等.而建模是一种重要的数学能力,对学生的分析、解决问题的能力要求较高,因此,教学中,应注重围绕具体教学内容,积极开展数学建模教学活动,提高学生的建模能力,为学生数学成绩的提高奠定基础.
一、函数模型的构建教学
函数是高中数学的重点知识,贯穿整个高中阶段.为提高学生函数模型构建能力,教学中,一方面,为学生深入讲解高中数学中各种函数模型,使学生掌握不同函数的性质以及相关结论,为函数模型的构建做好铺垫.另一方面,依托具体例题讲解,使学生掌握不同函数模型特点,以及构建模型的技巧,如注意找到正确的定义域.
例如:某电脑生产商,生产一品牌电脑的成本为4500元/台.研究发现,当销售价为6000元/台时,月销售a台.如价格提高的百分率为x(0 为构建正确的函数模型,教学中应引导学生找到月利润与销售之间的关系,显然月利润=月销售量×(售价-成本).显然提价后每台电脑的价格为6000(1+x)元/台.对应的月销售量为a(1-x2)台.于是不难构建如下模型: y=a(1-x2)[6000(1+x)-4500]=1500a(-4x3-x2+4x+1)(0 不等式是高中数学的重要知识点,是高考的必考点.不等式模型构建教学中,一方面,引导学生认真读题,搞清楚参数间的关系,设出合理的参数,构建正确的模型.另一方面,求解不等式模型式模型时,需要注意定义域,看等号成立的条件是否在定义域内,如不在应运用函数单调性知识进行求解. 教学中要求学生认真阅读题干,搞清题意,找到参数间的关系.设总能耗为f(x),根据题干描述,可构建的不等式模型为: 高中数学涉及的数列模型为等差与等比数列模型,因数列知识较为抽象,学生构建数列模型出错率较高,因此,教学中,一方面,引导学生分析等差与等比数列模型的区别,认真审题,找到能体现出“等差”或“等比”模型的描述,确定数列的首项以及公差或公比.另一方面,数列是特殊的函数,因此,在求解数列模型时,虽然可以应用函数知识进行探讨,但需要注意数列的取值为正整数. 例如,在讲解数列知识后,为学生讲解如下例题:某学校向银行贷款500万元准备建设一座可容纳1000人的学生公寓.工程于2018年初动工,年底准备交付使用.为偿还贷款(年利率5%,按复利计算),准备将公寓所收费用去除水电费、物业管理费共计18万元后,剩余部分全部用于偿还贷款.若公寓按照每生每年800元的标准收费,则哪一年可以将贷款还完?(已知lg1.7343=0.2391,lg1.05=0.0212). 因题目中明确给出按照复利计算,因此,该题目需要创建等比数列模型.设n年还完贷款.公寓每年收取的总费用是固定的,即为1000×800=80万元,去除物业费、水电费费用为18万元,因此,每年偿还的数额为80-18=62万元.则要想满足题意,构建如下模型: 62[1+(1+5%)+(1+5%)2+…+(1+5%)n-1]≥500(1+5%)n+1. 综上所述,高中数学教学中,为提高学生的建模能力,除要深入数学基础知识外,还应围绕具体例题讲解,使学生感受不同数学模型的构建过程以及注意事项,并鼓励学生积极总结建模技巧与方法,做到灵活应用.二、不等式模型的构建教学
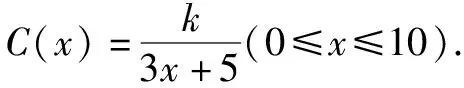
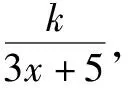
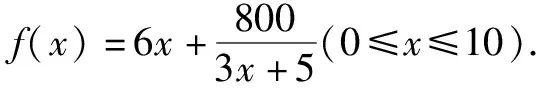
三、数列模型的构建教学

