10%+10%为什么等于0.11
2020-05-13章勤琼郭盼
章勤琼 郭盼

【摘 要】用手机计算器计算10%+10%,可以得到不同的计算结果,这是因为百分数有不同的意义。百分数在理论上具有与分数相同的各种意义,但考虑实际应用应该突出其表示两个量的比率关系的意义,这是百分数之所以产生的最大价值。在教学中,首先要加强对百分数意义的理解,特别是认识分数和百分数的异同。其次,将百分数的相关内容作为拓展资源,发展学生多方面的数学能力。
【关键词】百分数;百分率;意义;计算器
百分数的教学是小学数学教学中的一个重要内容,百分数在生活中的应用十分广泛。理解百分数的意义是学生学习百分数相关知识以及运用百分数解决有关实际问题的必备前提条件。[1]对于百分数参与运算的结果,存在不同意见。如10%+10%,大多数人认为可以转化成小数0.1+0.1,结果为0.2;也有人认为,百分数表示的是两个数的关系,不可以将其放在算式中进行运算,所以10%+10%没法计算。除这两种观点之外,利用手机计算器计算“10%+10%”,会出现不同的计算结果0.11。那么,10%+10%不同的计算结果指向小学阶段百分数的哪些意义?在教学中需要注意什么?我们应该对相关概念进行梳理,进而对教学有进一步的思考。
一、10%+10%为什么等于0.11
一般情况下,在进行有关百分数内容的计算时,需要先将百分数转化为分数或小数,再按照分数与小数的计算规则计算结果。如10%+10%=0.1+0.1=0.2,这样的计算并不存在什么难度,似乎也不应该有争议。然而,在用手机上的计算器对10%+10%进行计算时,却显示10%+10%=0.11。这样的结果显然是令人惊讶的。对于这个结果,该如何解释?
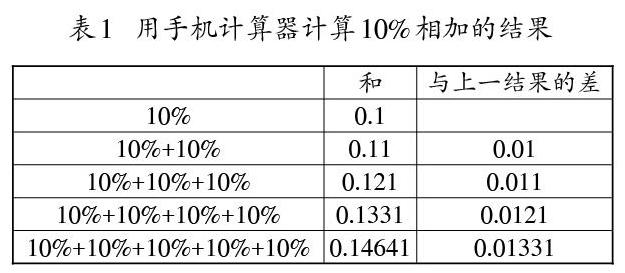
我们在计算时,按照小学数学四则运算的逻辑顺序,将10%看成[10100],也就是0.1,再做加减,结果为0.2。用计算器计算百分数的加法,之所以出现不同的结果,是因为百分号是个特殊的符号。百分数也叫百分率,这里的百分率是以哪个数为基数,也就是我们通常所说的单位“1”,即加上10%需要考虑的是加上哪个量的10%。计算出0.2的结果时,我们是将10%的单位“1”就当作数字1。然而,如果这里对10%的基数作不同的思考,就能得到10%+10%=0.11。如果继续加上10%,可以得到这样的结果:10%+10%+10%=0.121,10%+10%+10%+10%=0.1331;10%+10%+10%+10%+10%=0.14641……我们可以看出,后面所加的10%,都不是按照0.1的值来计算,每次加的10%的值分别是0.01,0.011,0.0121,0.01331,如果将增加的值与前面的和进行比较,可以得到如表1所示的结果。
通过对表1的观察,容易发现,每个算式与上一算式结果的差正好等于上一算式和的10%,即所加上的10%是以原来的加数作为基准量,即将原来的加数看作单位“1”,再加上这个数的10%。如10%+10%=10% ×(1+10%)=0.11,10%+10%+10%=(10%+10%)×(1+10%)=0.11×1.1=0.121……如果计算减法,也会得到类似的结果,如10%-10%=0.09,这是10%×(1-10%)的结果。而10%-10%-10%=(10%-10%)×(1-10%)=0.081。事实上,加上或减去一个百分数,可以这样计算:[a±b=a?(1±b%)],这里的[a]是指[±b%]之前所有的数的和。事实上,想利用手机计算器计算两个10%的数值的和,也是可以实现的。只需在10%外面分别加上括号就行,用手机计算器计算(10%)+(10%)的结果即为0.2,括号里面作为整体,自然不会以括号外面的结果作为基准进行百分率的计算。
因此,手机计算器的这种行为是对算法逻辑的不同选择,而不是计算错误。那为什么在手机计算器中一般要采用10%+10%=0.11这样的算法呢?最早的电子计算器并没有百分号“%”,后来加入之后,在一定程度上解决了计算场景中常有的难点。人们在日常生活中经常遇到计算小费、利息、折扣等场景,这样的计算逻辑会变得非常实用,而且更贴近人们的日常语言。例如,早餐8元,需要额外支付小费10%,利用计算器只需要输入“8+10%”,即可得到8.8元,而不需要输入“8+8×10%”或者“8×(1+10%)”,后面这两种输入,显然要烦琐得多,而且解释起来也更加复杂。这样的例子在生活中还有很多,如存入5000元,利息5%,到期所得只需输入“5000+5%”,就可算出5250元。减法也是如此,如某件商品500元,打八折销售,只需输入“500-20%”,就能得到400元。而讓计算器计算500-20%=499.8这样的算式,反倒没有什么实际意义。
如果用计算器来计算乘法和除法,跟我们习惯的运算结果没有差别,如10%×10%=0.01,10%÷10%=1。这是因为在乘除计算中,不需要涉及加上或减去哪个量的10%的问题,在生活中也不需要处理这样的场景。因此,如果了解百分数作为“百分率”的意义,并联系在生活中实际场景的实用价值,就能理解用手机计算器计算10%+10%为什么等于0.11。
二、小学阶段百分数的意义
百分数的英语为percentage,词根为“cent”,来自拉丁语centum(一百),percentage的意思为“每一百中的部分”。西方在15世纪就已经开始使用百分数的形式“per[co]”,在17世纪中叶的一本著作中,已经出现了用“per[oo]”的符号表示百分号,后来把前面的“per”也去掉了,而“%”这个符号的使用,则是现代的事了。[2]在数学辞海中,将“百分数”定义为一种特殊的分数,指分母是100的分数,或表示一个数是另一个数的百分之几的数。[3]之所以说百分数是特殊的分数,是因为百分数是分母为100的繁分数。当N是一个数时,繁分数[N100]通常读作百分之N,也写作N%。[4]这里的N可以是整数,也可以是小数和分数。跟平常一般需要将分数化简为分子分母为互质整数的最简分数不同,在百分数中,需要保证分母为100,至于分子是什么形式,并不重要。
