广义余弦函数及一类二阶抽象柯西问题研究

仓定帮，李庆庆，隋丽丽

(华北科技学院理学院，河北 三河 065201)

抽象空间中的算子微分方程初值问题是现代分析数学的一个重要的研究分支.其理论已经被广泛的应用于分布参数系统的研究.自Hille在1952年引入抽象柯西问题的概念后，众多的学者投身于该领域的研究.伴随着抽象柯西问题的研究不断深入，算子半群理论逐步成熟，强连续算子半群、积分半群等概念相继被提出，并在解决一阶抽象柯西问题中发挥着重要作用[1-7].在二阶抽象柯西问题方面，余弦函数理论起着类似作用[8-18].正如人们熟知，如下二阶抽象柯西问题：

(1)

(2)

及

(3)

系统(3)也被称为二阶广义参数分布系统，它比一般的参数分布系统应用范围更广，在复合热导体的温度分布、超导电路中的电压分布以及电缆系统中的信号传播等问题的研究中经常被设计.例如，考虑弹性奇异梁的振动问题，它的两个终端是固定的.这个问题的数学模型可以用下面的方程来描述：

(4)

其中，μ(t，x)∈Rn是位移向量，M(x)∈Rn×n是质量分布矩阵，通常为常数，是奇异的.f(x，t)是一个标量函数.方程(4)的边值边界条件为：

方程(4)可以用下面的Banach空间中的发展方程刻画，令

μ(t)∈H，Bμ(t)(x)=My(t，x)，

(5)

可以将(4)转化为(3)的形式.

本文借助算子半群相关理论，对抽象柯西问题(3)进行深入分析.实际上通过Laplace变换可得：

(6)

可以发现，要想通过Laplace变换解决问题(3)，可引入一类新的算子T(t)满足如下形式：

(7)

下文将该算子称为广义余弦函数，其生成元记为(A，B).本文第二部分给出了广义余弦函数的若干性质；第三部分讨论广义余弦函数扰动问题；第四部分和第五部分研究了广义余弦算子的遍历定理及问题(3)的适定性.

1 定义与性质

定义1B是Banach空间X中的有界线性算子，A是闭算子，ρ(B，A)={λ:λ∈C，(λ2B-A)-1}是X中的有界线性算子.令R(λ2B，A)=(λ2B-A)-1，将R(λ2B，A)称为广义正则集.

定义2B是Banach空间X中的有界线性算子，若有界线性算子{T(t):t≥0}满足T(-t)=T(t)且：

T(t+s)+T(t-s)=2T(t)BT(s)，t≥0，s≥0.

(8)

称T(t)为广义余弦函数.

例令

性质1设B是Banach空间X中的有界线性算子，A是闭算子，T(t)是广义算子半群，则

(9)

证明令Pλ=λ(λ2B-A)-1，则有

又有

同理

根据Laplace变换的唯一性，得证.

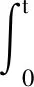
性质2假设T(t)是以(A，B)为生成元的广义余弦函数，若T(t)指数有界，则

证明因为

λ2R(λ2B，A)B=

R(λ2B，A)(λ2B-A+A)=I+R(λ2B，A)A，

性质3假设T(t)是以(A，B)为生成元的广义余弦函数，若T(t)指数有界，则

(10)

则

性质4假设T(t)是(A，B)以为生成元的广义余弦函数，则

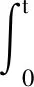
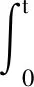
(11)

证明

又因为

再由Laplace变换的唯一性可以证得.

定理1设B是Banach空间X中的有界线性算子，A是闭算子，若存在常数M>0，使得

(12)

则存在一个广义余弦函数T(t)以(A，B)为生成元.

证明令ω′>ω，Γ=ω′+i∞，∀t≥0，定义

(13)

可以看出上面的积分在有限区间中是收敛的，再根据留数定理，可以得到：

得证.

2 逼近与扰动

定理2假设Tn(t)是以(An，Bn)为生成元的广义余弦函数，并且满足‖T(t)‖≤Meωt，若

证明因为

则据控制收敛定理可得

因为

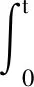
令x=(λ2B0-A0)-1y，则有

‖Tn(t)Bn(λ2Bn-An)-1y-

T0(t)B0(λ2B0-A0)-1y‖≤

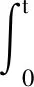
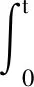
结合1)，2)以及

An(λ2Bn-An)-1=λ2(λ2Bn-An)-1Bn-I，

上式在n→∞时收敛于0，得证.

下面讨论广义余弦函数的扰动问题.假设T(t)是以(A1，B)为生成元的广义余弦函数，A2为线性算子并且满足

(14)

R(λ2B，A1+A2)=

(15)

证明因为T(t)是以(A1，B)为生成元的广义余弦函数，则

令Reμ>λ0，λ=λ0+ilmμ，则

R(μ2B，A1)=

R(λ2B，A1)[I+(μ2-λ2)BR(μ2B，A1)]，

且

再由定理(3)可得：

从而(A1+A2，B)也是某一余弦函数的生成元.

3 遍历定理

定义4假设T(t)是以(A，B)为生成元的广义余弦函数，定义

(16)

实际上可以证明P1=P2=P3.一方面，由

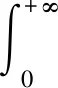
‖λ2R(λ2B，A)-P2‖=

定理5T(t)是以(A，B)为生成元的广义余弦函数，P是其阿贝尔遍历极限，则

1)PBx=BPx，P2Bx=Px;

2)N(A)⊆R(PB)，R(A)⊆N(PB)，

R(P)⊆N(A)，N(P)⊆P(A);

3)T(t)BPx=Px.

证明1)据AB=BA，有PB=BP，又∀x∈X，

2)另一方面，令x1∈N(A)，x2∈R(A)记x=x1+x2，存在y∈D(A)使得Ay=x2，进而

λ2(λ2B-A)-1Bx=

λ2(λ2B-A)-1B(x1+x2)=

λ2(λ2B-A)-1Bx1+λ2(λ2B-A)-1BAy=

(λ2B-A+A)(λ2B-A)-1x1+

λ2(λ2B-A)-1BAy=

x1+(λ2B-A)-1Ax1+

λ4(λ2B-A)-1B2y-λ2By→x1(λ→0)，

因为λ2A(λ2B-A)-1y=λ4(λ2B-A)-1By-λ2y,所以x∈D(A)且Ax=0，R(P)⊆N(A).进一步，∀x∈N(P)，有

-A(λ2B-1)-1x=

x-λ2B(λ2B-A)-1x→x，(λ→0)，

所以N(P)⊆R(A).

3) 根据定义3可得

4 抽象柯西问题

本节研究如下抽象柯西问题的适应性问题：

(17)

引理1[17]令Q，N，H为有界算子，对于如下抽象柯西问题：

定义R(λ2)∶=(λ2Q-λN-H)-1，若

则上述抽象柯西问题是适定的.

g(0)=0，y(0)=0,

则

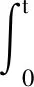
若Reλ>ω，

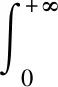
由Laplace变换的唯一性可得

y(t)=(λ2B-A)-1g(t)，y(t)∈D(A).

因而

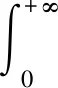
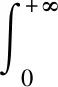
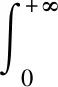
再由Laplace变换的唯一性可得

即问题(17)有解：

下面证明解的唯一性.假设μ1(t)，μ2(t)都是原问题的解，令υ(t)=μ1(t)-μ2(t)，则υ(t)满足：

再由引理1得到原问题有唯一零解，即μ1(t)=μ2(t).