面向输电线路的压缩感知图像去噪方法

王 娟，姜玉菡，陈泽昊，武明虎*，丁 畅，曾春艳，袁旭亮

(1.湖北工业大学湖北省能源互联网工程技术研究中心，武汉 430068;2.湖北工业大学太阳能高效利用及储能运行控制湖北省重点实验室，武汉 430068)

目前，由于图像采集设备分辨率和数据传输精准度的局限性，电力输电线路图像在采集与传输过程中难免受到噪声污染，导致当输电线路出现材料缺陷时检测不及时和识别率不高.在获取输电线路图像数据的流程中，人为操作、设备自身局限及复杂天气条件等因素都会导致各类噪声的出现.而高斯噪声在污染该类线路图像噪声中占比较高，因此对图像中的高斯噪声进行有效抑制，可改善高噪声下缺陷识别和定位的精确度较低的情况.

图像去噪作为压缩感知理论(compressive sensing)[1]应用主流方向，大致分为变换域滤波和空域滤波两个方面.空域滤波主要有非局部均值算法(NLM)[2]、三维块匹配(BM3D)[3]等方法对图像进行局部或非局部去噪；变换域滤波主要包括小波变换(wavelet)、Curvelet变换、Fourier变换[4]等.但多数传统算法无法在抑制噪声的同时使图像的细节获得较好的恢复，部分算法结合变换域滤波和空域滤波，仍存在算法复杂，运行占据较大内存，效率低等问题.而K-SVD算法[5]采用超完备字典[6-7]进行稀疏表达可有效利用图像结构信息，抑制高斯白噪声，减少算法复杂度，但含噪图像在采用超完备字典稀疏分解过程中，训练后的过完备字典下含有大量噪声原子，且容易造成图像平滑处边缘纹理缺失的问题.

为解决像素的噪音损坏程度取决于权重的自适应更新和高斯噪声问题，本文提出利用图像的非局部自相似性[8]信息作为正则化先验约束项，将其融入到K-SVD算法的稀疏表达中，从而建立输电线路图像噪声抑制模型.与传统滤波方法相比可以较好地保留边缘和纹理等重要信息，具有良好地自适应性[9]和更好的图像复原效果.

1 去噪模型的建立

1.1 K-SVD算法

K-SVD算法能够针对获取信号内容自适应训练字典原子获取超完备字典.由此建立起的噪声去除模型如下：

(1)

在非零元素约束下，稀疏表达阶段采取正交匹配追踪OMP(Orthonormal Matchin Pursuit)算法[10]，过度迭代选取字典原子：

(2)

其中，C为噪声增益，σ为噪声标准差，aij为稀疏表示系数.

字典学习过程中，算法迭代取决于全部残差与原子的内积.当该内积值小于某定值时，迭代过程将过早终止.为解决此类问题，本文提出使用分段弱共轭梯度追踪(Stagewise weak gradient pursuits，stWGP)算法[12-13].该算法中迭代定值选择原则符合弱选择特性，可选用为OMP算法框架下迭代终止的条件[11].该选择策略参考残差内积理论，构建内积极大值原子：

(3)

式中，0<α≤1，迭代阈值为

λk=αmaxjgk(j)|，

(4)

其中，λk为阈值，gk为残差卷积.在应用过程中，超完备字典的维数是无限的，而内积极大值原子却是有限的.两者的矛盾造成了迭代提前终止问题，本文使用的弱选择特性在该问题上表现良好.

传统K-SVD算法的样本训练时采用了大量噪声样本，导致训练的字典原子库中噪声原子占据了较大比例.若此时对噪声进行抑制，将会造成有用信号的提取障碍.因此，本文采用删减字典中噪音原子的策略，达到提升字典的目的.Bartlett M S在文献[14]中提出了Bartlett检验法.主要计算字典原子相异方向上的特征向量νi，并对相关性进行衡量：

(5)

噪声原子相异方向的相关性由于高斯噪声的随机分布趋近于为0.若满足Q<χ2(α:3)，则认定此单元完全为噪声，按照上述规则需要将其从字典库中删除.

1.2 输电线路图像的非局部自相似性

输电线路图像通常含有大量重复图像块，在局部区域中，图像块之间又存在若干相似块，被称为非局部自相似性先验(NSS)知识[15].考虑到图像块可作为多元变量向量样本采集，可将非局部自相似性先验训练图像块组，并应用于基于稀疏表达的字典学习当中.其中BUADES A等人提出图像噪声抑制方法利用了图像块的非局部相似特性[16]，为最大限度还原图像局部细节特征，对图像中冗余信息进行提取，并加权平均与该冗余具有相似邻域结构的像素，估计当前像素值.同时该像素点特征由待去噪像素点的邻域表征，以达到复原图像细节的目的.

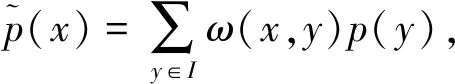
(6)

式中，权值ω(x，y)表示像素点x和y间的相似度，它的值由以x、y为中心的矩形邻域D(x)、D(y)间的距离‖D(x)-D(y)‖2决定：

(7)

当图像相似块占据较大比例时，该算法去除噪声效果明显.但是在一些相似块较少的特定的区域，该算法去噪效果不佳且对噪声鲁棒性较差.在此许多学者提出了改进框架，其中Ji Z等人根据信息的相似度而不是像素强度计算图像中每个像素的小局部窗口中的Zernike矩，得到更多具有更高相似性度量的像素或斑块[17].Zhang Q等人提出了一个新的框架，使用自适应非局部能量来规范成像线性逆问题，快速算法迭代地计算正则化过程，更有效的搜索相似图像块和计算权值[18].

2 算法实现过程

本文充分利用输电线路图像块中包含有丰富的非局部相似性信息，获取非局部自相似性先验数值，并融合高斯混合学习算法，提高数学模型的噪声抑制能力.

首先，对输电线路图像采用聚类方法展开训练.通过与分块组平均值作差，划分与输电线路图像范围内分组块近似的块组，从而得到非局部相似块.其次，将已聚类的分组与非局部相似块融合.再次，非局部自相似模型使用融合后的分组块训练.最后，二次训练后继续提取非局部相似块组.在此过程中，外部分块组的相似性度量准则使用马氏距离(Mahalanobis Distance，MD)分组.而图像内部分块组则采用先验知识引导聚类的方法，构建面向内部分块组的高斯混合学习方法，获得相似度较高的内部块.

因此，对采集到的含噪图像Y首先利用K-均值方法，引入图像外部分块组的先验指导.其次，搭建高斯混合学习方法训练内部分块组，并计算分块组平均值度量内部分组块相似程度.然后，围绕非局部块进行相似组块搜索，每个相似组块均算出最大平均值.最后，从输电线路图像中学习估计出非局部先验数值，内部分组块采取稀疏表达方式.

在稀疏表示中，稀疏系数向量符合拉普拉斯分布.因此，加权处理稀疏系数向量α，以获得权向量：

(8)

式中,c为常量；σ为噪声标准差.此过程中，需要引入自适应正则项替代加权稀疏编码模型最优化项[9]，并对先验指导模型训练中检索分组块进行加权处理：

W=exp(-με2),

(9)

式中，μ为正常数，编码残差ε去除图像噪声[15].

本文在高斯噪声的抑制过程中，字典与正则化项由高斯混合算法训练获得，而噪声抑制的工作则由加权稀疏表达来完成.为了更好地抑制高斯噪声，加权稀疏表达中的自适应正则化项融合了图像的先验知识，通过训练得到互正交字典，自适应地选出局部K-SVD字典.

优化权重矩阵W、编码残差ε的计算在K-SVD字典学习迭代过程中进行.建立非局部正则化项：

(10)

在模型(1)中图像复原效果不明显的原因在于：图像内部信息仅仅利用超完备字典进行稀疏表达，噪声与图像局部平滑方式相同.本文算法则受先验指导启发，融合K-SVD字典与非局部自相似性，对噪声和缺陷对象采用不同的平滑方式构建输电线路图像噪声抑制模型对图像进行复原.对此，本文加大了采集图像获取先验知识的权重，而后将其作为正则化制约代入图像噪声抑制中，方法构建如下：

ϑ‖ω(α-τ)‖1).

(11)

上述方法在计算过程中可转化为两个层次的最优化问题：

(12)

(13)

表1 算法流程Tab.1 Algorithm flow

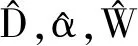
(14)

3 实验数据及结果

本文将提出的去噪方法与目前较为常用的BM3D、传统DCT字典、及给定超完备字典的K-SVD算法、改进小波算法[19]、WNNM算法[20]进行性能比较.实验数据集由6种200余张图像组成.其中，包括典型自然图像Lena、Boat、Peppers等，以及输电线路含有断股、磨损、气泡等典型现场捕获图像.高斯噪声等级分为σ=10、25、50三组，样本尺寸均为512×512，窗口尺寸为8×8.

3.1 不同高斯噪声等级的图像去噪效果对比

如图1所示，高斯噪声设置等级σ=10.在主观视觉效果上，人物的头发、帽檐相较其他算法具有更为清晰的纹理特征.采用工业输电线路中断股、磨损、气泡图像测试过程中，可以看出本文算法针对图像细节方面有所改善，特殊纹理信息和边界轮廓保留复原程度良好.

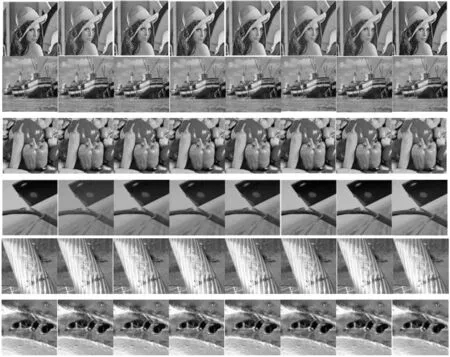
(a)原图;(b)加噪;(c)DCT去噪;(d)K-SVD去噪;(e)BM3D去噪;(f)小波算法;(g)WNNM算法;(h)本文算法图1 σ=10时去噪效果对比Fig.1 Comparison of denoising effect when σ=10

如图2所示，高斯噪声设置等级σ=25.从主观视觉角度可知，相较于其它算法存在的边界轮廓不清晰问题，本文算法具有较明显的边界复原效果，有效改善了噪声与图像局部细节平滑方式相同造成的细节模糊化问题.本文算法噪声抑制后的图像比另外五种更为清晰，高斯噪声的抑制效果较为明显.由表3中工业输电线路缺陷图像实验数据表明，改进后的模型在PSNR性能指标上与另外五种相比平均增加了1.52 dB左右.

如图3所示，高斯噪声设置等级σ=50.自然图像boat与线路磨损检测图像具有纹理细节显著、边缘轮廓清晰等特点.而从实验结果可以看出，本文算法能够很好地适用于此类图像中高斯噪声抑制，保证边缘和纹理细节的完整性，最大程度保留重要信息.同时，从工业输电线路断股、磨损、气泡等缺陷图像实验结果可看出，其它算法在高噪声下存在纹理模糊、边缘缺失等问题.而本文算法解决了高噪声下误将图像信息当作噪声处理的问题，边缘和纹理复原较为明显.

3.2 图像去噪质量评价

为了进一步验证本文所提出算法的去噪效果，选取峰值信噪比(PSNR)和结构相似度(SSIM)两个指标进行比较，从客观数据上比较分析所提出的算法性能，如表2和3所示.本文算法与性能最佳的比较算法在PSNR指标上平均增长了0.53～0.82 dB左右，SSIM指标上也不相上下.

(a)原图;(b)加噪;(c)DCT去噪;(d)K-SVD去噪;(e)BM3D去噪;(f)改进小波算法;(g)WNNM算法;(h)本文算法图2 σ=25时去噪效果对比Fig.2 Comparison of denoising effect when σ=25

(a)原图;(b)加噪;(c)DCT去噪;(d)K-SVD去噪;(e)BM3D去噪;(f)小波算法;(g)WNNM算法;(h)本文算法图3 σ=50时去噪效果对比Fig.3 Comparison of denoising effect when σ=50

表2 自然图像的各算法测试对比数据Tab.2 Natural image algorithms test and compare data

综上所述，当含有高斯噪声等级较高时，提出的改进算法重构图像的边缘细节清晰，主观视觉效果良好，能自适应解决噪声图像平滑处特征模糊化以及将图像信息当作噪声处理的问题.对三种典型缺陷去噪的PSNR值平均提高1.83 dB，SSIM值平均提高0.01.因此，本文算法能够有效的应用于含有不同高斯噪声等级的工业输电线路噪声抑制场合中.

4 结语

针对工业输电线路缺陷识别中存在的高斯噪声干扰问题，本文提出了一种非局部自相似特性和加权稀疏表达相融合的噪声去除算法.在算法构建过程中，OMP算法迭代阈值选择和终止条件遵循弱选择特性.同时采用Bartlett检验法删除K-SVD字典原子库中噪声原子，并高效使用图像非局部自相似性融入正则化约束相似性度量过程中，利用加权稀疏表达使算法具有更突出的复原效果.与典型去噪算法对比，该算法能最大限度地保留图像边缘细节和纹理信息等特征，去噪效果明显.但在提升复原能力的同时加重了算法的复杂程度，未来将着重改善算法效率.