地区人力资源对人均GDP的作用机理研究
——基于武汉市数据
2020-06-18吕小柏
吕小柏,李 钊
(武汉科技大学管理学院,武汉 430081)
前人从资源角度对人力资源的研究由来已久,研究也相当充分;从经济角度对劳动生产率、人力资本等要素的研究也比较充分,如学者孙浦阳的研究[1];从区域经济角度探讨经济发展与就业、人口状况、人力资本及社会稳定的关系的研究也不少,如学者张智敏的研究[2]、郭凯明的研究[3],等等.但比较少见的是将人力资源—经济发展的源头与人均GDP—经济发展的结果相联系的研究.
人均GDP是衡量一个地区经济发展水平的常用指标,也是基础性指标.人力资源作为基础的资源要素支撑着地区经济的发展.研究人力资源与人均GDP之间的关系,搞清楚它们是如何发生作用的,本研究认为很有必要.只有明白了两者间的作用机理才能在区域管理中有的放矢,少走弯路.
武汉市是我国中部最大的城市,有着复杂的经济系统和多元的经济结构,承担着国家发展的战略任务.选取武汉市数据作为研究素材,一是因为其统计数据较为完整连续,便于做定量分析,二是因为其复杂的经济体系及人力资源状况具有代表意义.本研究所用数学工具及方法均来自李红松、邓旭东主编的《统计数据分析方法与技术》[4].
1 研究指标
1.1 选取研究指标
一个地区的地区生产总值(Gross Domestic Product,GDP)是公认的衡量该地区经济社会发展的最重要的经济指标,本研究从人均GDP入手,分层构建分析指标,并利用Eviews 9.0软件和武汉市二十五年的统计数据做定量定性分析,探究一个地区的人力资源对人均GDP的作用机理.本研究所用数据均取自《武汉市统计年鉴》.
依照人均GDP的含义将其进行如下分解:
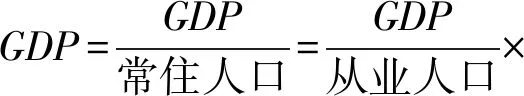
(1)

人均GDP=劳动生产率×就业率×
劳动适龄人口率=LP×LU×WR.
(2)
公式(2)将人均GDP这一基础指标分解为LP、LU、WR三个二级分析指标,而这三个指标都是人力资源相关指标,(2)式将经济指标与人力资源指标关联起来.本研究以公式(2)为主线,通过分析武汉市劳动生产率、就业率和劳动适龄人口率三项指标与人均GDP的关系展开研究.
1.2 确定分析变量
根据前人的研究和相关理论的叙述,并考虑实际需要,本研究将LP、LU、WR三个指标的影响因素做了概括并认为,影响LP的因素主要有产业集聚、资本深化、产业结构、工资水平等;影响LU的因素主要有工资水平、宏观经济状况、产业结构、人口结构等;而影响WR的主要因素有户籍适龄人口数量和常住外来人口数量.
具体地,产业集聚因素用产业密度(industry density)来表示,即各产业就业人数与武汉市城市面积之比,其中,第一产业、第二产业和第三产业的产业密度本研究分别表示为ID1、ID2、ID3.资本深化因素用劳均投资(investment per worker)来表示,即总投资额与劳动人口数量之比表示为IPW.产业结构(Industry Structure)因素用各产业产值占城市总产值的比例来表示,第一产业、第二产业、第三产业的结构因素分别表示为IS1、IS2、IS3,因为有IS1=1-(IS2+IS3),所以本研究只需取IS2和IS3两个变量.工资水平因素用城镇非私营单位年均工资表示,并用城镇居民消费价格指数将名义平均工资调整为实际平均工资(real average wage)表示为RAW.宏观经济状况因素用地区生产总值的增长率(growth rate)来表示即GR.
本研究认为人口结构因素由两个变量构成,即户籍劳动适龄人口(registered working-age population)RWAP和外来劳动适龄人口(immigrant working-age population)IWAP.按照我国现行标准,男性16~59周岁,女性16~54周岁为劳动适龄人口.由于统计口径的偏差,本研究做以下假设:假设武汉市常住外来人口均为劳动适龄人口.这是一种与实际情况近似的假设.虽然外来劳动适龄人口是常住外来人口的一部分,但由于外来人口到武汉市最主要的目的是就业,尽管其中有随迁的未成年人和退出劳动力市场的老人,但主体部分是劳动适龄人口.在此假设下,外来劳动适龄人口IWAP可以用常住外来人口(immigrant population)即 IP表示,其数据可在《武汉市统计年鉴》上获得.
本研究所涉及的指标、变量名称及符号如表1所示.
2 构建分析模型
2.1 劳动生产率LP模型
由本研究2.2知,劳动生产率LP与ID1、ID2、ID3、IPW、IS2、IS3、RAW七个分析变量有关.为了将各分析变量之间的单位差异标准化并减少异方差性,且不改变原分析变量的基本性质,将以上ID1、ID2、ID3、IPW、IS2、IS3、RAW七个分析变量及LP取自然对数,所形成的新变量为lnLP、lnID1、lnID2、lnID3、lnIPW、lnIS2、lnIS3、lnRAW,其中,lnLP为被解释变量,lnID1、lnID2、lnID3、lnIPW、lnIS2、lnIS3、lnRAW七个变量为解释变量.

表1 指标、变量名汇总表Tab.1 Names of index and variable
对新变量做单位根检验.单位根检验主要有Dickey-Fuller检验(DF检验)和Augmented Dickey-Fuller检验(ADF检验).由于当随机扰动项存在自相关时,DF检验会出现偏差,因此本研究采用ADF检验并运用Eviews 9.0软件实现.表2是各变量的ADF检验结果.
由表2得知,变量lnLP、lnID2和lnRAW为二阶单整,变量lnID1和lnIPW平稳,其余变量都是一阶单整,因而不能直接做协整检验.为了解决单整阶数不一致的问题,分别取lnLP、lnID2和lnRAW一阶差分,将三个二阶单整变量降阶为一阶单整变量,再次形成的新变量为DlnLP、DLnID2和DlnRAW,而此时变量DlnLP、DLnID2和DlnRAW的实际意义为lnLP、lnID2和lnRAW的增长率.对于变量lnID1和lnIPW,由于ADF检验结果显示为平稳,本研究不再考虑它们对LP的影响.

表2 ADF检验结果Tab.2 ADF test results
说明:1、(C,K,T)表示ADF检验中是否包含常数项、时间趋势项以及滞后期数;I(n)的括号中表示单整阶数,I(0)表示平稳.2.表中的检验值均取小数点后两位,并进行四舍五入.3、结论的得出以5%为临界水平.以上说明下同.
于是满足一阶单整的变量有被解释变量DlnLP,解释变量DlnID2、lnID3、lnIS2、lnIS3和DlnRAW.将这六个变量用Johansen方法进行协整检验,选择有截距无时间趋势和有截距有随机时间趋势的检验形式,用Eviews9.0软件实现检验.两种检验形式的迹检验和做大特征根检验结果均表明,在5%的显著性水平下,被解释变量DlnLP和各解释变量之间均存在三个协整方程.因此说明上述变量之间存在协整关系.
建立回归方程.本研究采用普通最小二乘法即OLS方法建立回归模型,并设定为以下形式:
DlnLP=β1+β2DLnID2+β3lnID3+
β4lnIS2+β5lnIS3+β6DlnRAW+μt.
(3)
(3)式中βi为常数项、μt为随机波动项.
用Eviews 9.0软件生成DlnLP,DlnID2、lnID3、lnIS2、lnIS3,DlnRAW的OLS回归模型,得到结果如表3所示.

表3 OLS 回归结果Tab.3 OLS regression results
对表3的回归结果进行序列自相关的LM检验及带交叉项的White异方差检验,检验结果表明在5%的显著性水平下,不存在自相关及异方差.因此,各变量的显著性系数有效.但表3显示,DLnID2、DlnRAW的t统计量的伴随概率(0.378 0、0.160 6)均远大于0.05,表明它们对被解释变量DlnLP的影响不显著,各变量之间可能存在严重的多重共线性,采用方差扩大因子法进行进一步检验.具体地,将每个解释变量分别作为被解释变量都对其它解释变量进行回归,得出可决系数R2的值,并依此计算方差扩大因子的数值.检验结果如表4所示.
表4显示,lnID3、lnIS2、lnIS3的方差扩大因子远远大于10,表明存在严重的多重共线性,这里采用逐步回归法解决变量的多重共线性问题.在经过一元回归、二元回归、三元回归、四元回归后,最终满足要求并被保留的解释变量有三个,分别为lnIS2、lnID3和lnIS3.
将解释变量lnIS2、lnID3和lnIS3与被解释变量DlnLP用OLS进行回归模型的估计,得到的结果如表5所示.
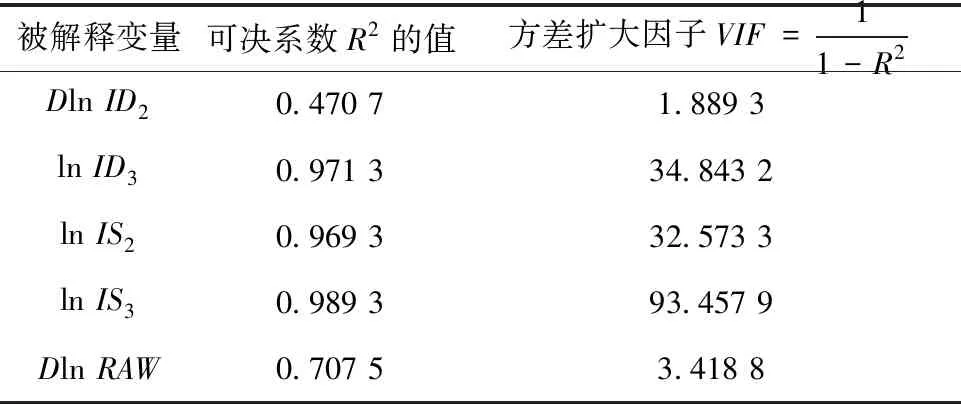
表4 方差扩大因子法检验结果Tab.4 Test results of the expanded variance factor method
注:以上数值均为四舍五入后的近似值.下同.

表5 OLS 回归结果Tab.5 OLS regression results
模型的估计结果为:
DlnLP=-14.0027+2.7335lnIS2+
1.6235lnIS3-0.4788lnID3.
(4)
(4.6656) (0.8030) (0.1568) (0.6315)
t=(-3.0013)(3.4040)(-3.0542)(2.5709)
F=10.2038,DW=1.9385.

2.2 就业率LU模型
由本研究1.2知,就业率LU与RAW、IS2、IS3、RWAP、IP、GR六个分析变量有关.为了将各分析变量之间的单位差异标准化并减少异方差性,且不改变原分析变量的基本性质,将以上RAW、IS2、IS3、RWAP、IP、GR六个分析变量及LU取自然对数,所形成的新变量为lnLU、lnRAW、lnIS2、lnIS3、lnRWAP、lnIP、lnGR,其中,lnLU为被解释变量,lnRAW、lnIS2、lnIS3、lnRWAP、lnIP、lnGR六个变量为解释变量.
对新变量做单位根检验.各变量的ADF检验结果如表6所示.

图1 模型的实际值、拟合值和残差图Fig.1 Map of actual value,fitting value and residual
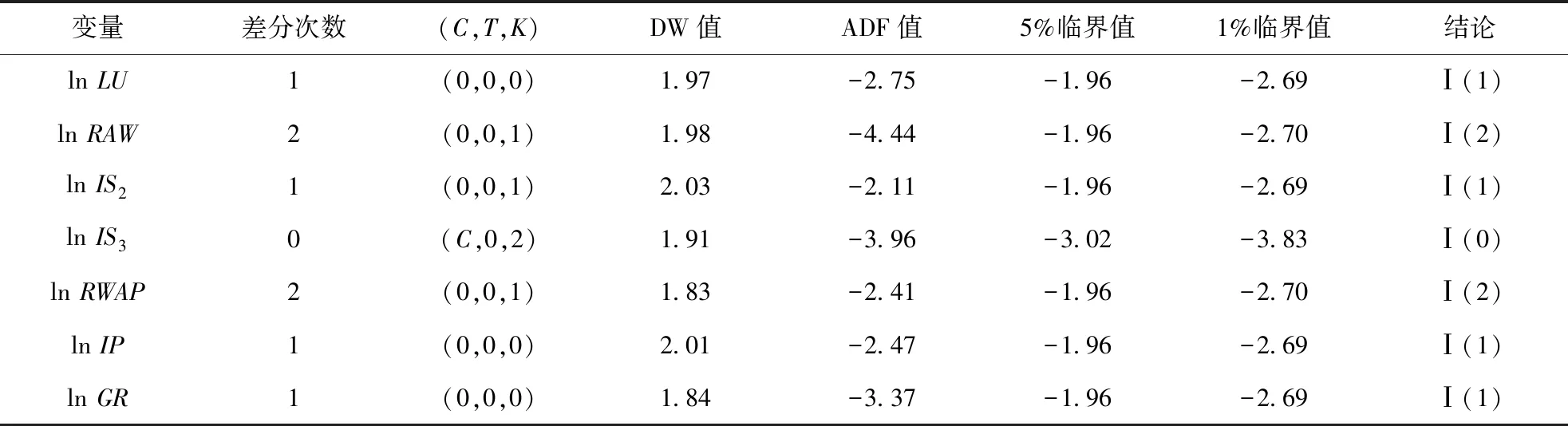
表6 ADF检验结果Tab.6 ADF test results
说明:lnRAW、lnIS2、lnIS3的检验结果与表2存在差异是由于样本数量变化所致.
表6显示,变量lnRAW和lnRWAP为二阶单整,变量lnIS3平稳,其余变量都是一阶单整,因而不能直接做协整检验.为了解决单整阶数不一致的问题,分别取lnRAW和lnRWAP一阶差分,将两个二阶单整变量降阶为一阶单整变量,再次形成的新变量为DlnRAW和DlnRWAP,而此时变量DlnRAW和DlnRWAP的实际意义为lnRAW和lnRWAP的增长率.对于变量lnIS3,由于ADF检验结果显示为平稳,本研究不再考虑它对LU的影响.
于是满足一阶单整的变量有被解释变量lnLU,解释变量DlnRAW、lnIS2、DlnRWAP、lnIP和lnGR.将这五个变量用Johansen方法进行协整检验,选择有截距无时间趋势和有截距有随机时间趋势的检验形式,用Eviews 9.0软件实现检验.在5%的显著性水平下,有截距无时间趋势的协整检验表明各变量之间至少有五个协整方程,有截距项有随机时间趋势的协整变量表明各变量之间至少有六个协整方程,因此说明上述变量之间存在协整关系.
建立回归方程.采用OLS方法建立回归模型,并设定为以下形式:
lnLU=β1+β2DlnRAW+β3lnIS2+
β4DlnRWAP+β5lnIP+β6lnGR+μt,
(5)
式中,βi为常数项,μt为随机波动项.
用Eviews 9.0软件生成lnLU、DlnRAW、lnIS2、DlnRWAP、lnIP、lnGR的OLS回归模型,得到的结果如表7所示.
对表7的回归结果进行序列自相关的LM检验及带交叉项的White异方差检验,检验结果表明在5%的显著性水平下,不存在自相关及异方差.因此,各变量的显著性系数是有效的.但表7显示,DlnRWAP的伴随概率(0.134 5)大于0.05%,表明它对被解释变量lnLU的影响不显著,各变量间可能存在多重共线性,采用方差扩大因子法做进一步检验.各变量的可决系数和方差扩大因子的结果如表8所示.
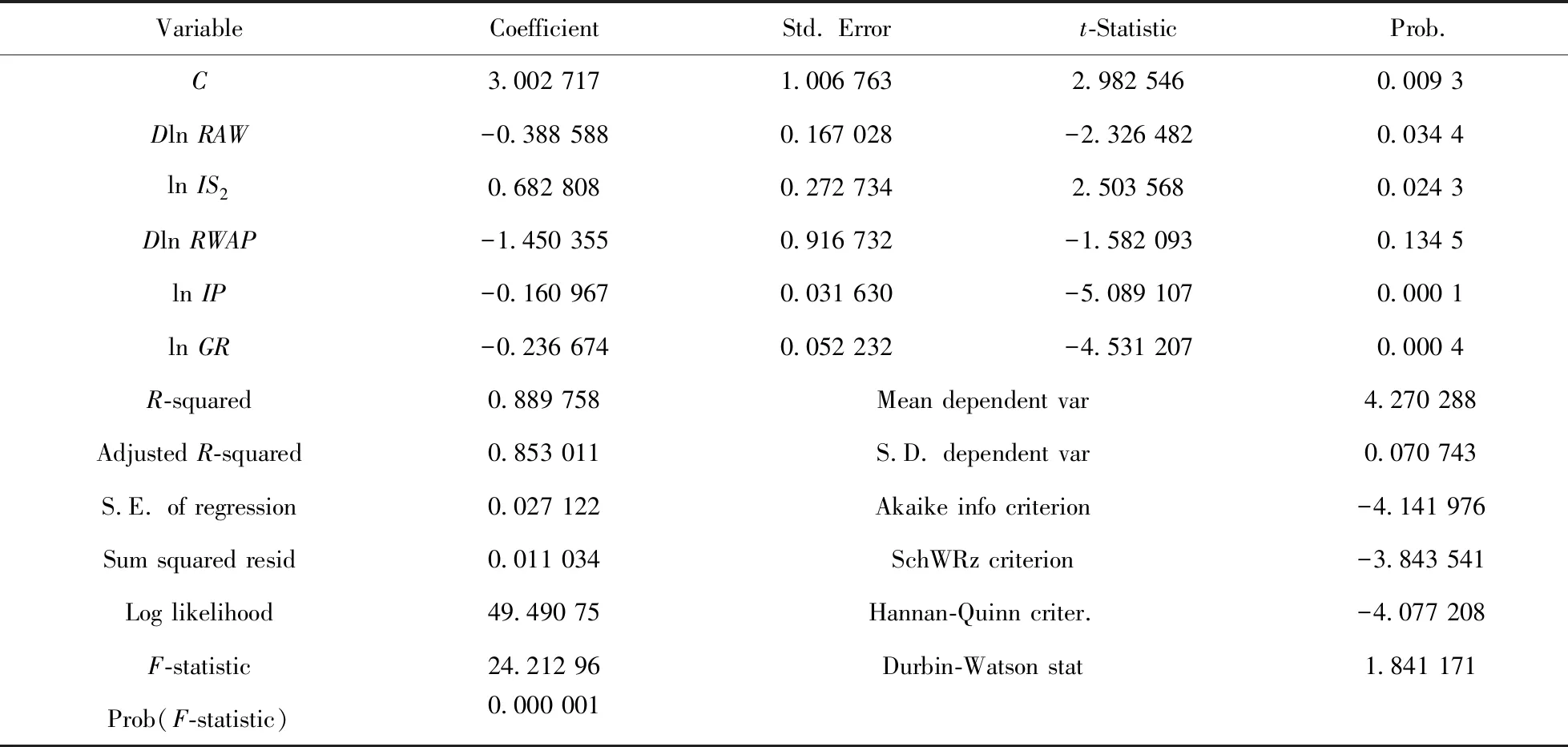
表7 OLS 回归结果Tab.7 OLS regression results

表8 方差扩大因子法检验结果Tab.8 Test results of the expanded variance factor method
lnIP的方差扩大因子与10极其接近,表明上述变量存在相当程度的多重共线性.这里采用逐步回归法补救变量的多重共线性.在经过一元回归、二元回归、三元回归、四元回归后,最终满足要求并被保留的解释变量为lnIS2、DlnRAW、lnIP、lnGR.于是,被解释变量lnLU回归模型的估计和Eviews 9.0软件的输出结果如表9所示.

表 9 OLS 输出结果Tab.9 OLS output results
由于(5)式模型取过一次差分,调整后的样本个数变为21年,查5%显著水平的DW统计表可知dL=0.927,dU=0.812,因此有dL lnLU=2.1923-0.4431DlnRAW+ 0.8368lnIS2-0.1201lnIP-0.2212lnGR. (6) (0.9065)(0.1709) (0.2665)(0.0191) (0.0537) t=(2.42)(-2.59)(3.14)(-6.29)(-4.12) F=27.0952,DW=1.561221. 图2 模型的实际值、拟合值和残差图Fig.2 Map of actual value,fitting value and residual (7) (7)式为恒等式,本研究取其作为劳动适龄人口率WR的分析模型. 根据第2章、第3章的分析,可得以下四个模型,以此理清人力资源对人均GDP的作用机理. 人均GDP=劳动生产率(LP)×就业率(LU)×劳动适龄人口率(WR), (8) DlnLP=-14.0027+2.7335lnIS2+ 1.6235lnIS3-0.4788lnID3, (9) lnLU=2.1923-0.4431DlnRAW+ 0.8368lnIS2-0.1201lnIP-0.2212lnGR, (10) WR=户籍劳动适龄人口率+ 外来劳动适龄人口率. (11) (8)式揭示了人均GDP与劳动生产率、就业率和劳动适龄人口率有直接关系.劳动生产率是通过其水平的变化作用于人力资源需求端,从而影响人力资源需求与供给关系的,劳动适龄人口率是从人力资源供给端直接影响人力资源需求与供给关系的,就业率则是人力资源供需匹配程度的反映.由此可得,人力资源是通过劳动生产率、就业率与劳动适龄人口率三因素作用于人均GDP的. (9)式是对劳动生产率所做的深入解析,它揭示了影响劳动生产率的主要因素及其影响水平与方向.(b)式明显地反映出地区(武汉市)劳动生产率(DlnLP)第二、第三产业产值比率(lnIS2、lnIS3)关,其中第二产业(Coefficient 2.733478)对劳动生产率的影响远大于第三产业(Coefficient 1.623496),说明长期以来地区(武汉市25年间)劳动生产率的增长主要依赖第二产业.(b)式还显示,第三产业密度(lnID3)与生产率(DlnLP)关.由于第三产业是向社会提供服务的产业,而服务主要依赖人的劳动,一个地区第三产业密度的高低决定了其所需人力资源的多少,因而第三产业密度的变化将引起该地区对人力资源需求的变化.总之,第二、第三产业产值比率(lnIS2、lnIS3)三产业密度(lnID3)的均通过引起劳动生产率要素(DlnLP)化最终在人均GDP上得到反映. (10)式是对就业率进行的深入解析.(武汉市)就业率(lnLU)与第二产业产值比率(lnIS2)正相关,与城镇非私营单位年均工资增长率(DlnRAW)、常住外来人口(lnIP)和地区生产总值的增长率(lnGR)相关,也即对就业率有影响的四个因素中只有第二产业产值比率一个因素对其有正向作用,说明(武汉市25年间)就业率严重依赖第二产业.而城镇非私营单位年均工资、外来人口以及地区生产总值的过快增长都会降低地区(武汉市)就业率,其中城镇非私营单位年均工资增长率(Coefficient -0.4431)对就业率的负影响远远大于另两者.城镇非私营单位年均工资是地区人力资源价格的重要标量,有很强的示范作用.人力资源价格(工资)的增长会导致各行业对人力资源需求的较少,从而降低地区就业率. (11)式是对劳动适龄人口率做进一步的解析,说明户籍劳动适龄人口与外来劳动适龄人口共同构成了一个区域的人力资源供给.显然,户籍劳动适龄人口与外来劳动适龄人口同时增长对人均GDP的正向影响作用大,但就目前各地区情况看,两者同时增长的情况少见.由于受劳动力价格的牵引,发达地区外来劳动适龄人口在增长,欠发达地区增长的户籍劳动适龄人口部分流向发达地区,因此,增长的人力资源供给推高了发达地区的人均GDP. 综上分析,本研究得出以下四点主要研究结论. 1) 劳动生产率、就业率和劳动适龄人口率对人均GDP的影响呈乘数效应,三因素中任何一个因素的变化都将引起人均GDP的巨大变化. 2) 劳动生产率是人力资源作用于人均GDP的媒介.劳动生产率与第三产业的产业密度负相关,第三产业密度又影响着其对人力资源的需求,也就是说,人力资源通过第三产业密度的变化引起劳动生产率的变化,最终作用于人均GDP. 3) 就业率是人力资源通过价格作用于人均GDP的结果反映.第二产业的发展对就业率是有明显的正向作用的,但人力资源价格(工资)的过快增长会兑冲第二产业发展的正向作用,导致就业率的下降,最终引起人均GDP的变化. 4) 劳动适龄人口率是人力资源由供给端作用于人均GDP的要素.在本地区人口增长降低,人力资源供给不足的情况下,只能靠外来人力资源(外来劳动适龄人口)支撑人均GDP的增长. 由于本研究依赖武汉市25年的统计数据,因此本研究对武汉市及与武汉市规模相当产业结构相似的城市更有实践意义.由此,本研究形成以下两点结论. 1) 类似于武汉市,如果一个地区第二产业产值率对劳动生产率贡献较大(如(b)式提示),而就业率又主要依赖第二产业(如(c)式提示),势必导致地区人力资源向第二产业过度供给,势必抑制其它产业对人力资源的需求而影响其它产业发展,其结果可能导致地区产业类型转化及提升变得困难. 2) (10)式提示,类似武汉市这样的国有经济成分占比重的城市,要想提高地区就业率必须放慢城镇非私营单位年均工资的增长速度;同时就业率的增长还要求放慢地区经济增长速度以调整产业结构.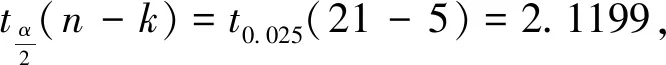

2.3 劳动适龄人口率WR模型


3 分析及结论
3.1 模型分析
3.2 主要研究结论
3.3 其它研究结论
