型不变量为(e，3，1)的有限正则非交换p群的分类

张 慧 玲

(太原学院应用数学系，太原 030001)

正则p群的概念和理论是Hall在1933年提出并发展的，在以后的半个世纪中，人们对这个理论做了不少有价值的工作，使它形成了p群理论中一个重要的研究方向.其中一个重要的理论就是Hall在文[1]中给出的基定理，从而正则p群的分类问题要比一般的p群分类相对容易.对于型不变量为(e1，…，ew)的正则p群，记w(G)=w，如果w(G)=1，则G循环，如果w(G)=2，则G是亚循环的，而亚循环p群的分类已知[2-3]，剩下最简单的情况就是w(G)=3，即型不变量为(e1，e2，e3)的有限p群.文[4]分类了型不变量为(e，1，1)的正则p群，文[5]分类了型不变量为(e，2，1)的正则p群，本文将分类型不变量为(e，3，1)的正则p群，由于p7阶群的分类已由文[6]完成，所以只需要考虑e≥4的情形，而型不变量为(4，3，1)的有限p群不一定亚交换，从而换位子计算非常复杂，故本文只给出p≥5时型不变量为(e，3，1)的正则p群的分类.由文[7]定理5.2.10可知，正则2群是交换群，而型不变量为(e，3，1)的有限交换p群只能是Cpe×Cp3×Cp，故本文只考虑型不变量为(e，3，1)的有限正则非交换p群，其中p≠2．

本文用到一些具体的符号，其中G′表示群G的导群，Z(G)表示群G的中心，expG表示群G的方次数，d(G)表示群G的秩，Φ(G)表示群G的Frattini子群，N≤G表示N是群G的子群，G/N表示群G关于群N的商群，o(b)表示b的阶，〈a，b〉表示由a，b生成的群，i(G)=〈gpig∈G〉，Ωi(G)=〈g∈Ggpi=1〉，其它符号和术语均是标准的．

1 预备知识

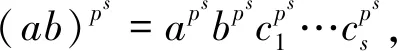
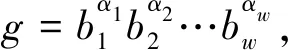
定义3[7]设G是有限正则p群，令Wi(G)=1(G)Ωi(G)，0≤i≤e，称群列G=We(G)≥We-1(G)≥…≥W0(G)=1(G)为G的W群列.在W群列中去掉重复项，再加细成G到1(G)间的一个主群列：G=L0(G)>L1(G)>…>Lw(G)=1(G)，称为G的一个L群列．

定义4[7]设G是有限正则p群，expG=pe.对于1≤s≤e，令pws(G)=Ωs(G)/Ωs-1(G)|，称(w1，w2，…，we)为G的w不变量，其中ws=ws(G).另外，对于任意的正整数j，1≤j≤w，令ej为在集合(w1，w2，…，we)中≥j的元素个数，这样得到一组正整数e1≥e2≥…≥ew，称它们为G的e不变量或型不变量．

下面介绍本文所用到的一些结果.

引理1[7]设G是有限p群且s(G′)=1，则G是ps正则的当且仅当G是ps交换的．

引理2[7]设G是ps交换p群，则s(G)=Z(G)．

引理3[7]设G是有限正则p群，expG=pe，e≥0，则：

2)Ωi(G)=〈g∈G|gpi=1〉={g∈G|gpi=1}，其中0≤i≤e；

4)api=bpi⟺(ab-1)pi=1⟺(a-1b)pi=1，其中0≤i≤e；

5) [api，b]=1⟺[a，b]pi=1⟺[a，bpi]=1，其中0≤i≤e；

引理4[7]设G是有限正则p群，(L)为G的任一个L群列.对于1≤i≤w，取bi是Li-1(G)Li(G)中任一最小阶元素，则(b1，…，bw)是G的一组唯一性基底．

2 型不变量为(e，3，1)的正则非交换p群

定理1设G是型不变量为(e，3，1)(e≥5)的正则非交换p群，则G属于下述六类群之一：

Ⅰ 〈a，b，c|ape=bp3=cp=1，[b，a]=c，[c，a]=aipe-1bjp2，[c，b]=akpe-1bhp2，[b，ap]=[a，bp]=1〉，p≥3．

Ⅱ 〈a，b，c|ape=bp3=cp2=1，[b，a]=c，cp=aipe-1bjp2，[c，a]=akpe-1bhp2，[c，b]=alpe-1bmp2，[b，ap2]=[a，bp2]=1〉，p≥3，i、j模p不全为零.

Ⅲ 〈a，b，c|ape=bp3=cp3=1，[b，a]=c，cp=aipe-2bjp2，[c，a]=akpe-2bhp2，[c，b]=alpe-1，[b，ap3]=1〉，p≥3，(i，p)=1.

Ⅳ 〈a，b，c|ape=bp3=cp=1，[b，a]=aipe-1bjp2，[b，c]=akpe-1bhp2，[c，a]=alpe-1bmp2，[b，ap]=1〉，p≥3，i、j、k、h、l、m模p不全为零．

Ⅴ 〈a，b，c|ape=bp3=cp=1，[b，a]=aipe-2bjp，[b，c]=akpe-1bhp2，[c，a]=alpe-1bmp2，[b，ap2]=1〉，p≥3，i、j模p不全为零．

Ⅵ.〈a，b，c|ape=bp3=cp=1，[b，a]=aipe-3bjp，[b，c]=akpe-1bhp2，[c，a]=alpe-1bmp2，[b，ap3]=1，[b，ap2]=axpe-1〉，p≥3，(i，p)=1，(x，p)=1．

证明因为w=3，所以d(G)=2或3.取G的L群列：G=L0(G)>L1(G)>L2(G)>L3(G) =1(G).下面就d(G)=2和d(G)=3分别讨论.

1)d(G)=2

因为GL2(G)|=p2，故G′≤L2(G)，又1(G)≤L2(G)，从而Φ(G)≤L2(G)，进而有L2(G)=Φ(G).取a∈L0(G)L1(G)，b∈L1(G)L2(G)使o(a)=pe，o(b)=p3，则G=〈a，b〉，1(G)=〈ap，bp〉.令[b，a]=c，由引理3可知，o(c)=p，p2或p3.由且c∈1(G)知c∈L2(G)L3(G).断言G3≤1(G)：令1(G)则若交换，则G′≤1(G)；若非交换，则内交换，从而进而得证．

下按o(c)=p，p2和p33种情况讨论：

(1)若o(c)=p，由引理4知，(a，b，c)为G的U-基，由G′=〈cg|g∈G〉且G′正则知expG′=p，从而expG3≤p，又G3≤1(G)=〈ap，bp〉，于是G3≤〈ape-1，bp2〉.由此可得[c，a]=aipe-1bjp2，[c，b]=akpe-1bhp2.因为o(c)=p，由引理3知[b，ap]=[a，bp]=1，故G属于第Ⅰ类群.

(2)若o(c)=p2，因为cp∈1(G′)≤1(G)=〈ap，bp〉，从而cp=aipe-1bjp2，又expG′=p2，进而由引理1知G是p2交换群，由引理2知2(G)=〈ap2，bp2〉≤Z(G)，于是cp∈Z(G)，expG3≤p，又G3≤1(G)=〈ap，bp〉，从而G3≤〈ape-1，bp2〉，由此可得[c，a]=akpe-1bhp2，[c，b]=alpe-1bmp2.因为o(c)=p2，从而i、j模p不全为零且由引理3知[b，ap2]=[a，bp2]=1.故G属于第Ⅱ类群．

(3)若o(c)=p3，首先证明1(G)是p交换的.由G正则知1(G)正则，又bp3=1，由引理3知[bp，ap]p=1，于是有exp1(G′)=p，由引理1知1(G)是p交换的.再证cp=aipe-2bjp2.因为cp∈1(G′)≤1(G)，因此有cp=aipbjp.由1(G)是p交换的，可得cp3=(aipbjp)p2=aip3=1.从而pe-3|i.又cp2∈2(G′)≤2(L2(G))=3(G)=〈ap3〉，于是有cp=aipe-2bjp2.又o(c)=p3，故(i，p)=1.最后证明G3≤〈ape-2，bp2〉.因为exp1(G′)=p3，由引理1知G是p3交换的，再由引理2知3(G)=〈ap3〉≤Z(G)，进而cp2∈Z(G)，于是有expG3≤p2.令.容易验证为型不变量为(e-1，3，1)的正则p群.与o(c)=p2的论证类似，可知，从而G3≤〈ape-2，bp2，cp2〉=〈ape-2，bp2〉，设[c，a]=akpe-2bhp2，[c，b]=alpe-1bmp2.容易看出G′≤〈ape-2，bp2，c〉，即G′交换.由此可得[c，a，b]=[c，b，a]=1，进而有m≡0(modp).由e≥5，ap3∈Z(G)知ape-2∈Z(G)，从而[cp，b]=1，进而[cp，b]=1，于是有l≡0(modp).因为o(c)=p3，由引理3知，[b，ap3]=1.故G属于第Ⅲ类群．

2)d(G)=3

由引理4知，存在a∈L0(G)L1(G)，b∈L1(G)L2(G)，c∈L2(G)L3(G)使o(a)=pe，o(b)=p3，o(c)=p，(a，b，c)为G的U-基.因为Φ(G)=1(G)=〈ap，bp〉，所以G′≤〈ap，bp〉.又G′=〈[b，a]g，[b，c]g，[c，a]g|g∈G〉，o(b)=p3，由引理3知expG′≤p3．

下按expG′=p，p2和p33种情况讨论：

(1)若expG′=p，则G′≤〈ape-1，bp2〉.设[b，a]=aipe-1bjp2，[b，c]=akpe-1bhp2，[c，a]=alpe-1bmp2，于是i、j、k、h、l、m模p不全为零.再由引理3知[b，ap]=1.故G属于第Ⅳ类群

(2)若expG′=p2，则G′≤〈ape-2，bp〉，又o(c)=p，由引理3知[b，c]p=[c，a]p=1.设[b，a]=aipe-2bjp，[b，c]=akpe-1bhp2，[c，a]=alpe-1bmp2，于是i、j模p不全为零.因为expG′=p2，由引理3知[b，ap2]=1.故G属于第Ⅴ类群．

(3)若expG′=p3，则G′≤〈ape-3，bp〉，又o(c)=p，由引理3知[b，c]p=[c，a]p=1.设[b，a]=aipe-3bjp，[b，c]=akpe-1bhp2，[c，a]=alpe-1bmp2，于是(i，p)=1.又expG′=p3，由引理3知[b，ap3]=1.因为[b，ap2]∈[G，2(G)]=3(G′)≤3(G)=〈ap3〉 ，由引理3知[b，ap2]p=1，可设[b，ap2]=axpe-1，(x，p)=1，故G属于第Ⅵ类群．