大气中气溶胶颗粒对红外激光的散射特性研究

林 宏，周传璘，马洪华，陈 敏

( 湖北工程学院物理与电子信息工程学院，湖北 孝感，432000)

大气中CO2无节制的排放会引起全球范围内温度的上升，进而导致温室效应，使得冰川融化、海平面上升和严重干旱等极端气象频发，这些全球范围内的气象灾害将会严重威胁人类的生存和发展.世界各主要国家都已达成共识，通过采取积极措施，制定合理可行的碳排放标准，努力减少全球温室气体的排放.为了更好的制定国际碳排放标准，确定每个国家的责任和义务，需要能够给出各个国家和地区大气CO2浓度的准确数值.因此，世界上各主要国家和地区都把精确探测大气CO2浓度数据作为研究的关键.

由于激光雷达的发射功率非常高，不易受到大气环境的影响，而且具有空间距离分辨的能力，因此，利用激光雷达来实现大气CO2浓度的主动测量技术越来越受到人们的普遍重视.近年来，美国相关科研机构提出能够利用宽波段红外激光来实现大气CO2浓度的探测[1-3].由于普通差分激光雷达光谱较窄，需要将波长稳定在一个点上，而宽波段激光雷达的光谱较宽，对激光频率稳定的要求较低，同时能够克服普通差分激光雷达由于波长抖动带来的探测误差.国内相关科研机构也研制出用于大气CO2浓度探测的宽谱红外激光源[4-5].但是通常宽谱红外激光源的光谱范围有20 nm左右，而一般的地基探测激光雷达方程中的光学参数都是针对单一波长的，因此，需要研究在宽谱条件下各种光学参数是否有变化.除了在探测大气CO2浓度以外，利用红外激光探测其它大气成分的过程中，大气气溶胶颗粒的光学红外散射特性也是重要的研究对象，尤其是其散射系数和后向散射率特性对建立地基红外激光雷达探测方程有重要意义.但是由于大气中气溶胶颗粒的物理特性十分复杂，很难用严格的数学方程和数学模型来分析其光学散射特性，以至于难于准确计算出其散射系数和后向散射率的大小[6-8].

本文通过把大气气溶胶颗粒近似看成理想球体，利用米氏散射数学方程，建立了依据散射效率因子来计算大气气溶胶散射系数和依据散射相函数来计算大气气溶胶后向散射率的模型.通过分析大气中气溶胶颗粒在红外波段内的散射系数和后向散射率特性，为建立基于红外激光雷达的大气成分浓度遥感探测模型提供一定的理论基础.

1 大气激光雷达探测方程

对于普通大气激光雷达探测方程，造成激光探测信号在大气介质中能量衰减的主要原因有两个，一是大气气体分子、气溶胶等大气物质对光的吸收效应.单波长准直激光在大气媒质中经过dr距离后，损失的辐射通量为dF=-aFdr，该损失由吸收效应产生，大气总的吸收系数一般用a(m-1)来表示.大气中物质对光的吸收效应实际可以看成为进入大气媒质中的部分光子能量发生了改变，变成了动能、热能、化学能等.二是大气气体分子、气溶胶等大气物质对光的散射效应.单波长准直激光在大气媒质中经过dr距离后，损失的辐射通量为dF=-bFdr，该损失由散射效应产生，大气总的散射系数一般用b(m-1)来表示.大气物质对光散射作用表现为入射到大气介质中的部分光子与大气中气体分子或气溶胶颗粒等物质发生碰撞，从而严重偏离原来的运动轨迹，使得沿入射方向直线传输的光强度逐渐减小，相当于入射前集中的光子后来分散到很广的区域内.由于大气气溶胶颗粒的尺寸与大多数激光波长数量级相当，因此，相比于大气气体分子来说，大气气溶胶颗粒引起的大气散射效应更加明显.

大气介质总的衰减系数c(m-1)的定义为：当单波长准直光束通过大气介质时，总的衰减系数等于其吸收系数与散射系数之和.光在大气中的衰减是由大气中的粒子对光子的吸收和散射作用引起的，表现为沿入射方向直线传输的光强度大小变化情况.理论上，普通地基激光雷达探测方程的一般表达式为[9-10]：

(1)

(2)

式中，c=a+b为大气总的衰减系数；a为大气中总的吸收系数；b为大气中总的散射系数.

普通地基激光雷达由于都采用单一波长激光进行探测，上述激光雷达方程中的物理量都为单一确定值.但是采用宽谱激光雷达进行探测时，探测激光不再是单一波长，而是宽谱激光，因此普通地基激光雷达方程中的部分系数可能有所变化，还是不是单一确定值，需要进行研究分析.特别是普通地基激光雷达方程中后向散射率γb、吸收系数a和散射系数b都是与探测激光波长有关的物理量，因此需要在宽谱激光波长范围内对上述大气参数进行研究分析，看是否有变化、具体数值为多少.对于大气中总的后向散射率和总的散射系数来说，大气中气溶胶颗粒的散射影响占主要地位，因此本文重点研究在宽谱红外激光波长范围，大气中气溶胶颗粒的散射特性，分析其后向散射率和散射系数变化的情况，为建立大气成分红外激光雷达探测方程提供理论依据.

2 大气气溶胶散射特性

大气中气溶胶颗粒对探测激光的散射特性主要由两个重要参数决定，一是其散射系数，反映气溶胶颗粒引起入射光偏离原来的传输轨迹，使得直线传输的光强度呈衰减变化；二是其后向散射率，反映气溶胶颗粒对光产生散射作用时，后向的散射能量占全部散射能量的比例.在利用地基宽谱激光雷达探测大气CO2浓度时，通常是通过检测大气中的激光后向散射回波信号，来实现对大气CO2浓度信息的获取，因此后向散射率的大小直接影响探测精度和有效探测距离.

大气组成成分十分复杂，主要包含各种气体和悬浮微粒等.通常把悬浮在大气中的固态和液态颗粒物总称为大气气溶胶.大气总的散射系数主要是由大气中各种气体分子的散射系数和大气气溶胶颗粒的散射系数组成.当研究入射激光与媒质中颗粒的相互影响时，如果媒质中颗粒半径(r)和入射激光波长(λ)的比值r/λ≪1时，就会发生瑞利散射效应，散射光的强度随着入射激光波长的四次方增加而减小.瑞利散射光强呈对称分布状态，且分布均匀.如果r/λ≈1时，就会发生米氏散射效应，散射光的强度随着入射激光波长的平方增加而减小.米氏散射光强度呈不对称分布状态，且分布不均匀.米氏散射主要集中在前向散射部分，后向散射部分较弱.如果r/λ≫1时，属于漫反射范畴，可用几何光学理论来处理.当入射激光波长远远大于大气气体分子的尺寸时，主要发生瑞利散射现象，可以利用瑞利散射方程很精确地计算出大气中各种气体分子的散射系数.而大气中气溶胶颗粒由于密度、大小、分布极其复杂，其严格描述理论还不存在，本文拟根据大气中气溶胶颗粒的半径与入射激光波长在一个数量级的特点，可以把大气气溶胶颗粒近似看成理想球体，利用米氏散射方程来描述其散射特性.根据等效球的米氏散射理论，大气中气溶胶颗粒的散射系数可描述为[11-12]：

b=K0N(πr2)，

(3)

式中，K0为其散射效率因子，它与气溶胶颗粒的半径、气溶胶颗粒的折射率和入射激光波长有关；N为气溶胶颗粒的密度；r为气溶胶颗粒的半径.

通常，散射效率因子K0等于散射截面σs与颗粒几何截面πr2之比.当球形颗粒半径为r，入射光波长为λ时，无偏振自然光的散射截面σs可以用下式来计算[13-15]：

(4)

此时，散射效率因子K0可以表示为：

K0=σs/πr2=

(5)

式中,an，bn称为米氏散射系数.可以利用下列公式分析得出：

(6)

(7)

其中：

(8)

(9)

另外，在计算大气气溶胶颗粒的后向散射率时，必须首先求出其颗粒的散射相函数.大气气溶胶颗粒的散射相函数反映了气溶胶颗粒在0°～360°一个完整圆周范围内，不同角度上散射光强所占比例的大小.根据米氏散射数学模型，散射相函数P(θ)可用下式计算得到[13-15]：

P(θ)=4πa(θ)/σs,

(10)

式中，θ为散射角度；a(θ)为某个方向上的角散射截面；σs/4π为各个方向上的角散射截面总和的均值.其中，角散射截面a(θ)的计算公式为：

(11)

其中,S1，S2可用下列无穷级数表示：

(12)

(13)

上两式中的πn、τn只与散射角θ有关，即[16-18]：

(14)

(15)

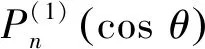
根据米氏散射数学模型，利用大气气溶胶颗粒P(θ)函数的计算公式就可以推导计算出相应的后向散射率.大气气溶胶颗粒的后向散射率γb等于其散射光在90°到270°范围内光强的总和比上散射光在0°到360°范围内的总和，通常可以用下式来计算：

(16)

式中，θ为散射角的大小，P(θ)为气溶胶颗粒的散射相函数.

3 仿真结果及其分析

本文重点针对适用于大气CO2浓度探测的红外激光光谱范围内，对大气中气溶胶颗粒的散射效率因子及其散射系数特性进行分析，分析结果对于该波段范围内的大气其它成分激光雷达探测也同样适用.通常大气中气溶胶颗粒的半径大约在0.001～100 μm之间，其一般折射率约为1.50-0.0119i左右[19-20]，但是用于探测大气CO2浓度的红外激光波长约在1.6 μm左右，根据光学散射原理可知，只有介质颗粒大小和入射光波长可相比拟时，才能利用米氏散射理论分析其散射特性，而且只有大气中液体型气溶胶的微粒一般才呈球形.因此，本文在研究大气气溶胶颗粒散射系数的相关特性时，只针对半径范围在0.1～10 μm的液体型气溶胶颗粒，在探测波长为1 568～1 585 nm的近红外光作用下的散射效率因子K0进行了仿真计算，得到下列仿真图形：

通过分析上述图形可以发现：此类大气气溶胶颗粒在1 568 nm处的散射效率因子与在1 585 nm处的值差别不大，可以看成一个定值；在探测波长一定时，随着气溶胶颗粒半径r的增大，散射效率因子K0的数值出现振荡衰减的现象，最终稳定于数值2.04处.

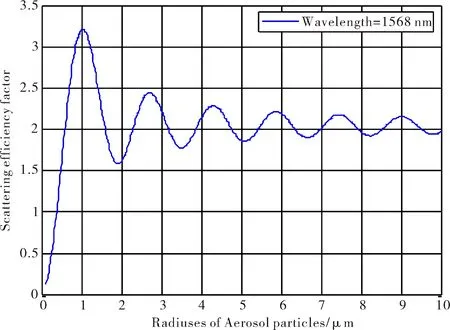
图1 波长为1 568 nm时的散射效率因子Fig.1 Scattering efficiency factor of 1 568 nm wavelength

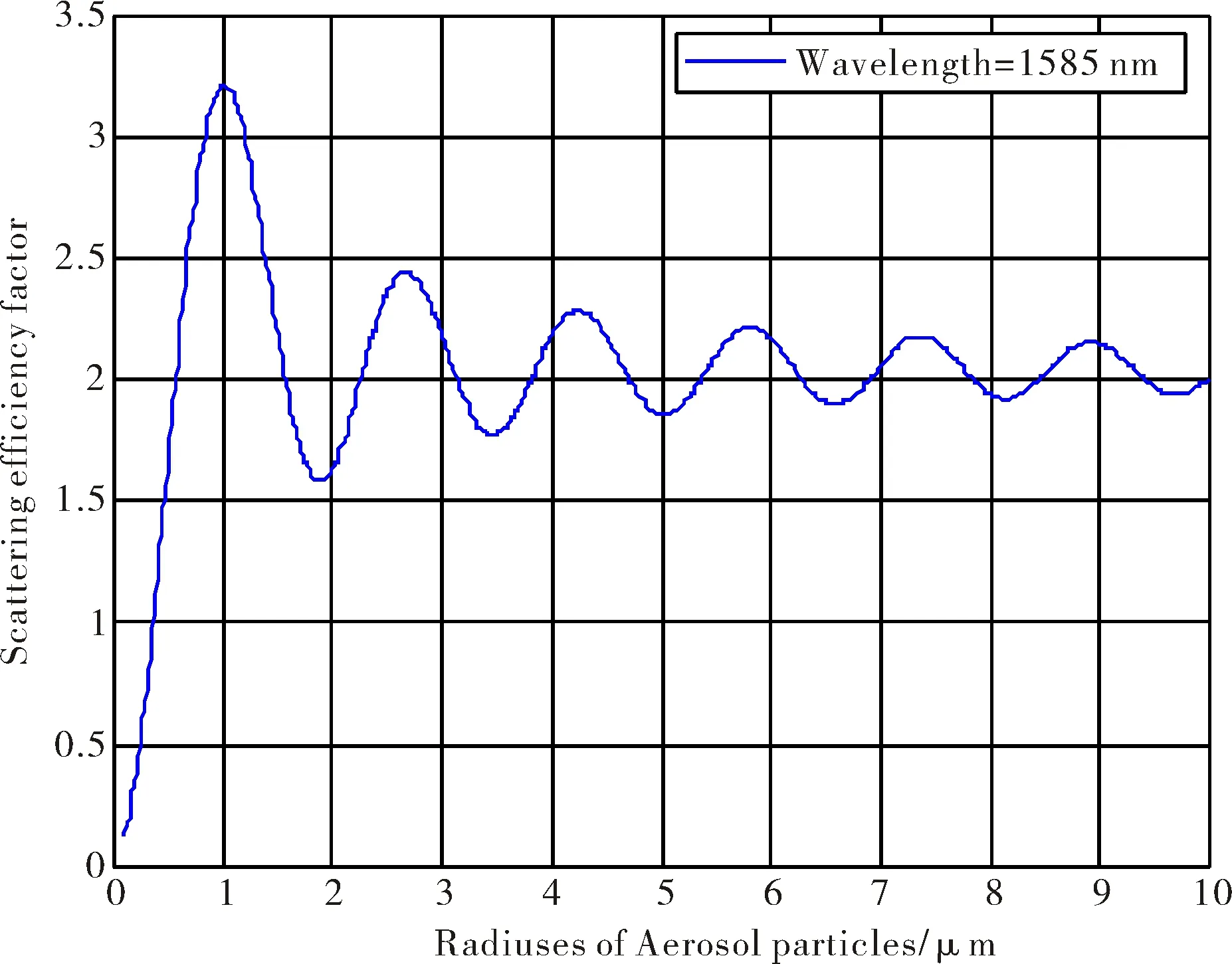
图2 波长为1 585 nm时的散射效率因子Fig.2 Scattering efficiency factor of 1 585 nm wavelength

根据等效球的米氏散射理论，本文首先计算出大气气溶胶颗粒的K0数值，接着根据公式(3)就可以计算出在1 568～1 585 nm光谱范围内，大气气溶胶颗粒散射系数b的数值.本文设定的仿真系数为：大气气溶胶颗粒半径r为0.1～10 μm；大气气溶胶颗粒密度N为1×103～1 000×103cm-3.在此条件下，计算得到的此类大气气溶胶颗粒散射系数如表1～表3所示.

表1 不同密度情况下0.1 μm气溶胶颗粒的散射系数Tab.1 Scattering coefficient of 0.1 μm aerosol particles

表2 不同密度情况下1 μm气溶胶颗粒的散射系数Tab.2 Scattering coefficient of 1 μm aerosol particles

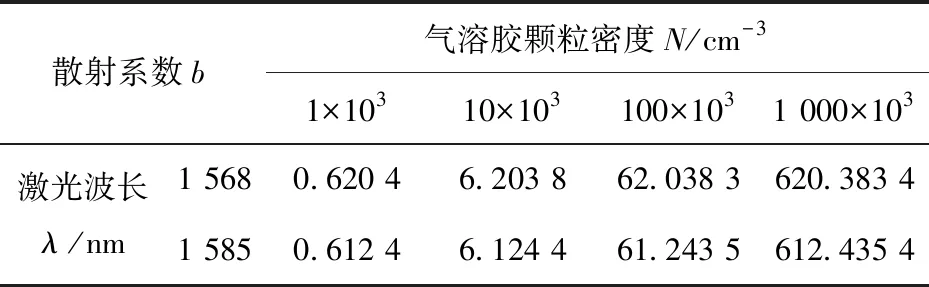
表3 不同密度情况下10 μm气溶胶颗粒的散射系数Tab.3 Scattering coefficient of 10 μm aerosol particles

由上述3个表可以得到：当入射激光波长不变、颗粒半径r恒定时，此类大气气溶胶颗粒的散射系数b正比于颗粒密度N的大小；当入射激光波长不变、颗粒密度N恒定时，此类大气气溶胶颗粒的散射系数b正比于颗粒半径r的大小；在1 568～1 585 nm的光谱范围内，激光探测波长的变化对气溶胶颗粒的散射系数b的数值影响很小.

本文设定的仿真参数为：大气气溶胶颗粒的半径r为0.1～10 μm；入射激光波长λ为1 568～1 585 nm.通过仿真计算得到液体型大气气溶胶颗粒的P(θ)函数的结果如图3和图4所示.

图3 1 568 nm处的散射相函数分布图Fig.3 Scattering phase function at 1 568 nm

图4 1 585 nm处的散射相函数分布图Fig.4 Scattering phase function at 1 585 nm

分析上述图形可以发现：在1 568～1 585 nm的光谱范围内，激光探测波长的变化对气溶胶颗粒的散射相函数影响不大，影响大气气溶胶颗粒散射相函数数值的主要因素是粒子的半径；此类大气气溶胶颗粒对光的散射效应都集中在前向(0°～90°)方向上，后向(90°～180°)方向上的散射相对较小；当入射激光波长恒定时，0°～10°区间内的前向散射强度正比于气溶胶颗粒半径的增加，同时150°～180°区间内的后向散射强度也正比于气溶胶颗粒半径的增加.

本文设定的仿真参数为：整个散射范围的散射角取值为0°～360°；后向散射范围的散射角取值为90°～270°.通过仿真计算可以得到此类大气气溶胶颗粒后向散射率γb的结果如下所示：

由上表可知：在1 568～1 585 nm的红外光谱范围内，气溶胶颗粒半径与激光探测波长相当时，探测波长的变化对此类大气气溶胶颗粒的后向散射率影响不大，在气溶胶颗粒半径为10 μm时，由于半径数值超过探测波长较多，几何散射效应明显，而米氏散射效应减弱，引起计算误差增加；当入射激光波长恒定时，此类大气气溶胶颗粒的后向散射率γb反比于颗粒半径r的变化.

4 结论

根据等效球的米氏散射理论，分别提出了利用散射效率因子计算大气气溶胶颗粒散射系数和利用散射相函数计算其后向散射率的方法.利用米氏散射理论及其递推计算公式，分别仿真了在1 568～1 585 nm的红外光谱区域内液体型大气气溶胶颗粒的散射效率因子和散射相函数的数值.仿真结果表明，在1 568～1 585 nm的红外光谱范围内，气溶胶颗粒半径与激光探测波长相当时，激光探测波长的变化对此类大气气溶胶颗粒的散射系数和后向散射率影响不大，可以近似看成一个定值；当此类大气气溶胶颗粒的半径逐渐变大时，其散射效率因子K0的数值发生振荡衰减现象，最终稳定于数值2.04处；此类大气气溶胶颗粒的后向散射率随着粒子半径的增大而减小.仿真结果和理论推导为建立基于红外激光雷达的大气成分浓度遥感探测模型提供了一定的理论基础和技术指导.