含阻尼连接的侧框架支撑作用下高耸塔器结构的动力特性研究

张贵辰，张宏涛，刘应华

(1.北方工业大学 电气与控制工程学院，北京 100043；2.北方工业大学 土木工程学院，北京 100043；3.清华大学 航天航空学院，北京 100084)

0 引言

石化高塔结构为了抵御风载荷作用，一般需要附加支撑框架结构增加动力稳定性，如图1所示。但是由于框架结构与塔结构存在耦合作用，而且塔结构内部会产生高温或者化学反应，产生变形，因此框架和塔结构一般不是直接连接，而是采用限位连接，这样会不可避免产生碰撞，导致塔器结构的破损。本文提出利用粘滞阻尼连接在框架和塔结构之间来减少塔结构在风载荷作用下的动力反应。这类结构可以简化为悬臂梁与支撑梁通过阻尼连接，对该类结构的动力特性研究较少，包括阻尼系数、支撑刚度与悬臂梁刚度之比、支撑位置等都需要进行优化。

图1 化工框架塔结构示意

Wang[1]利用传递矩阵法建立了考虑弹性支撑刚度和位置的Euler梁振动频率求解方程，结果表明，一个弹性支撑下基频要达到最高频率，支撑位置必须在无支撑自由梁振动的二阶振型零点处。Wu等[2]建立了均匀悬臂梁在多个弹簧和阻尼支撑作用下的自由振动和受迫振动特性的解析数值结合求解法，约束梁的振动可以通过自由梁的频率和振型叠加求解。Main等[3]利用无约束框架和刚性约束框架的振动特性，得到了含阻尼约束框架的振动特性，并且确定了优化的阻尼参数和位置。Pierson等[4]指出带有弹簧支撑梁的振动特性已经得到了解决，但是对于带阻尼约束的梁还没有有效而简单的解决方法，提出了利用振型叠加法来求解阻尼梁的频率和振型，并且发现悬臂梁的阻尼约束最佳位置与弹簧支撑的最佳位置相同，也在悬臂梁振动的二阶振型零点。Chen等[5]建立了含位移和转动约束拉伸梁的振动特性，并利用迭代数值算法进行了求解。Zhang等[6]利用传递矩阵法解决了弹性支撑作用下两根梁的动力特性问题。Li等[7]分析了两根梁在连续黏弹性支撑作用下的振动问题。Mao等[8]研究了弹性基础作用下的双梁结构在轴力作用下的动力特性。Fei等[9]得到了弹性支撑双梁结构的半解析解。Huang等[10]利用弹性支撑双梁结构得到了索支撑梁结构的频率和振型，并进行了支撑位置和参数优化分析。在高耸塔器工程应用方面，彭恒等[11]以某高101 m的石化解析塔器为研究背景，进行风振模拟及其采用侧向支撑的减振计算分析，设计在塔器和侧框之间采用阻尼器连接并在工程中应用，塔器减振取得了较好的效果；谭蔚等[12]以某公司的催化裂化装置为原型，按照2∶1的缩放比例建立高40 m的底部框架试验塔，研究结果表明，在底部框架塔中安装橡胶阻尼器可有效减小底部框架塔在横风向振动下的塔顶振幅，提高设备的安全性。

综合以上分析，对于阻尼和框架支撑同时存在情况下，如何分析框架刚度和阻尼参数对梁振动特效的影响还没有相关研究，而这对于本文开始提出的高耸塔结构问题尤为重要。本文利用传递矩阵法得到含框架支撑和阻尼连接的高耸塔结构的振动频率和振型计算表达式，然后利用该方法对框架塔结构进行动力特性分析，得到不同框架支撑和阻尼参数组合作用下的动力解。

1 含框架支撑和阻尼的高耸塔动力特性分析

经典阻尼理论(也称为比例阻尼)在结构动力分析中普遍采用，但对于具有附加阻尼器的结构来说，这种假设通常是不成立的。在经典阻尼系统中，模态形状不受阻尼力的影响，从而允许运动方程转化为一组，使用无阻尼系统的自由振动模态形状的独立模态方程可进行求解。在求解解耦中，结构中的阻尼分布必须通过Caughey等[13]所建立的条件与质量和刚度的分布相匹配。由于侧框架塔附加阻尼器通常设置在结构内的几个不同位置，阻尼力与质量或刚度分布不匹配。因此，采用无阻尼自由振动形状模态通常不能用于解耦结构的运动方程与附加阻尼器。为此，Rayleigh等[14]提出了表示阻尼的另一个常见假设，即：结构承受到轻微阻尼[15-17]时，不限制阻尼力的分布，设阻尼力是一个低阶数量级，远小于惯性力和刚度力，且阻尼引起的本征频率和振型的扰动也假设为小量；在上述假设下，每个固有频率由反映无阻尼耗散的虚部来修正，而模态曲线形状，通过与无阻尼模态形状正交的虚部来修改每个模态形状。

本文利用传递矩阵法得到含框架支撑和阻尼连接的高耸塔结构的振动频率和振型计算表达式，设ωk为第k阶复数频率，可表示为实部和虚部形式：

(1)

根据Euler-Bernoulli振动理论方程如下：

(2)

即:

(3)

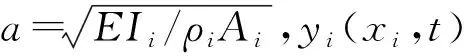
yi(x,t)=Yi(x)sin(ωt+φ)

(4)

将式(4)代入式(3)，求得特征函数Yi(x)方程如下：

Yi(x)=C1isinkixi+C2icoskixi+C3ishkixi+C4ichkixi

(5)

其中:

(6)

这里ω为结构体系的圆频率，k为ω的函数，Ci=(C1i，C2i，C3i，C4i)为积分常数。同时可以得到i段塔的转角、弯矩和剪力特征函数。

+C4ikishkixi

(7)

(8)

(9)

对图2所示带阻尼塔器结构①②建立连续条件，可以将弹簧和阻尼作为联合约束统一引入。

方程(10)～(13)分别为在连接点处位移、转角、弯矩和剪力连续条件，其中剪力连续条件为塔器结构①②在框架③支撑点以上处的剪力相同。

①②表示塔器结构分为两部分；③表示框架结构

(10)

Y′1(b)=Y′2(b)

(11)

Y″1(b)=Y″2(b)

(12)

EI1(x1)Y‴1(b)-[(KT1+cs1k)Y1(b)-(KT3+cs3k)Y3(b)]=EI2(x2)Y‴2(b)

(13)

对图2中塔器结构①②边界条件：

(14)

对图2中框架③边界条件：

(15)

将连续条件和边界条件组合在一起，形成求解频率的系数矩阵：

(16)

根据系数不为0的条件，确定行列式等于0，即可求得复频率，从而得到振型。

2 验证和讨论

以下首先与已有的有限元计算方法进行比较，从而验证本算法的正确性，然后运用文中的方法，计算高耸框架结构在各种不同参数组合下的结构动力特性，并找出一定的规律，得出相应的结论。

2.1 验证算法的正确性

首先利用本文方法对文献[2]中均匀悬臂梁连接阻尼的情况进行分析，如图3所示。相关参数为：梁长度l=1 m，分布质量ρA=0.675 kg/m,弹性模量E=7×1010N/m2，惯性矩I=5.20833×10-10m4，阻尼支撑位置b=0.2 m，阻尼系数ce0=5，10 N·s/m。文献[2]中的弹簧与地面的固定连接在本文中以框架刚度无穷大代替。采用本文提出计算方法与文献[2]提出方法和有限元计算方法进行比较，结果基本吻合，验证了本文算法的正确性。计算梁的一阶至三阶频率比较见表1。

图3 含阻尼支撑的均质悬臂梁结构示意

表1 本文方法与其他方法梁三阶频率计算比较

2.2 含阻尼和框架支撑高耸塔器分析

(2)高耸框架塔不同阻尼器参数和支座位置的固有频率。

表2 不同支撑位置、弹簧和阻尼参数下的固有频率

从表2中看出阻尼频率随支座位置和阻尼系数而变化，因此，将不同支座位置和阻尼参数的频率列于表3。当b=0.5L时，随着阻尼器参数的增加，基本阻尼频率(虚部)逐渐增大，直至刚性连接。当c0=10时，塔振动衰减率(实部)达到最大值，这意味着结构被过阻尼。第二阻尼频率先增加，第三阻尼频率随着阻尼器参数的增加而减小。

研究上述支撑位置在b=0.5L和b=0.78L处结果表明：当侧框架和塔单位质量抗弯刚度相同时，在支撑位置b=0.5L处采用不同的阻尼器参数可获得较好的阻尼频率值(7.15 rad/s)，而在支撑位置b=0.78L处阻尼频率仅3.90 rad/s。采用不同的支撑侧框架、支撑位置和阻尼器系数，结构的固有频率会有较大的变化，故采用本文中的求解方法可以很好地设计结构的固有频率。

表3 不同支座位置和阻尼参数的结构固有频率

2.3 弹性支撑和框架刚度对频率的影响

为了研究弹性参数k0、框架塔刚度比ab、支撑位置b对高耸塔结构频率的影响，得出如图4所示关系曲线。

图4 框架塔刚度比在不同弹簧连接情况下的基频

从图4可以看出，弹性参数k0=1时，无论框架塔刚度比ab和支撑位置b如何改变，基频都不会明显提高；k0=10，ab=1时，b>0.6L后，基频不会明显提高,ab=5时，随支撑位置提高基频有提高，但是ab>5后，同一支撑位置的基频不会明显提高；k0=100，ab=1时，b>0.6L后，基频反而明显减少，ab=5，b=0.6L比0.5L有提高，但是b>0.6L基频没明显提高，ab>5后，随着b提高基频会明显提高；框架与塔之间刚性连接，ab=1时，b>0.5L后，基频明显减少，ab=5时，支撑位置对基频影响不大，但是ab>5后，随着b提高基频会明显提高。综上所述，框架塔刚度比ab和支撑位置b以及弹性参数k0为3个相互耦合较强的参数，在k0，b为一定时，增加ab可以适当地增大结构的一阶固有频率；随着b的增加，根据ab和k0的不同，会导致结构一阶固有频率呈现单调上升或者单调下降。

3 结论

本文利用传递矩阵法得到含阻尼连接的侧框架支撑的高耸塔器结构的振动频率的计算表达式，并利用该方法对框架塔结构进行了动力特性分析，得到了不同框架支撑位置和阻尼、弹性参数组合作用下的动力解。在框架塔刚度比相等情况下，弹性支撑参数和阻尼参数为1时，频率差别不大，但是振型比较明显，阻尼连接会起到明显的减小振幅效果；框架塔刚度比和支撑位置以及弹性支撑参数对高耸塔结构的振动基频的影响效果明显，并为3个相互耦合较强的参数，故在实际的工程设计中，可以利用该方法在3个参数中1个或2个参数固定的情况下，可以较直观地搜索到更为优化的结构固有频率，对工程结构设计具有一定的指导作用；在高耸塔器的工程设计中，一般高耸塔器的周期较长、对外部激励反应强烈，通过增加侧框架能减少侧移，更有意义的是使塔器的周期减小，大幅降低动力响应。本文方法分析表明：侧框架支撑点在塔器1/2高度处比在塔器2/3高度处侧框架塔的频率提高约83%，考虑动力响应影响下侧框架的支撑点不宜过高，在塔器的1/2高度处设支撑点为优化参数。